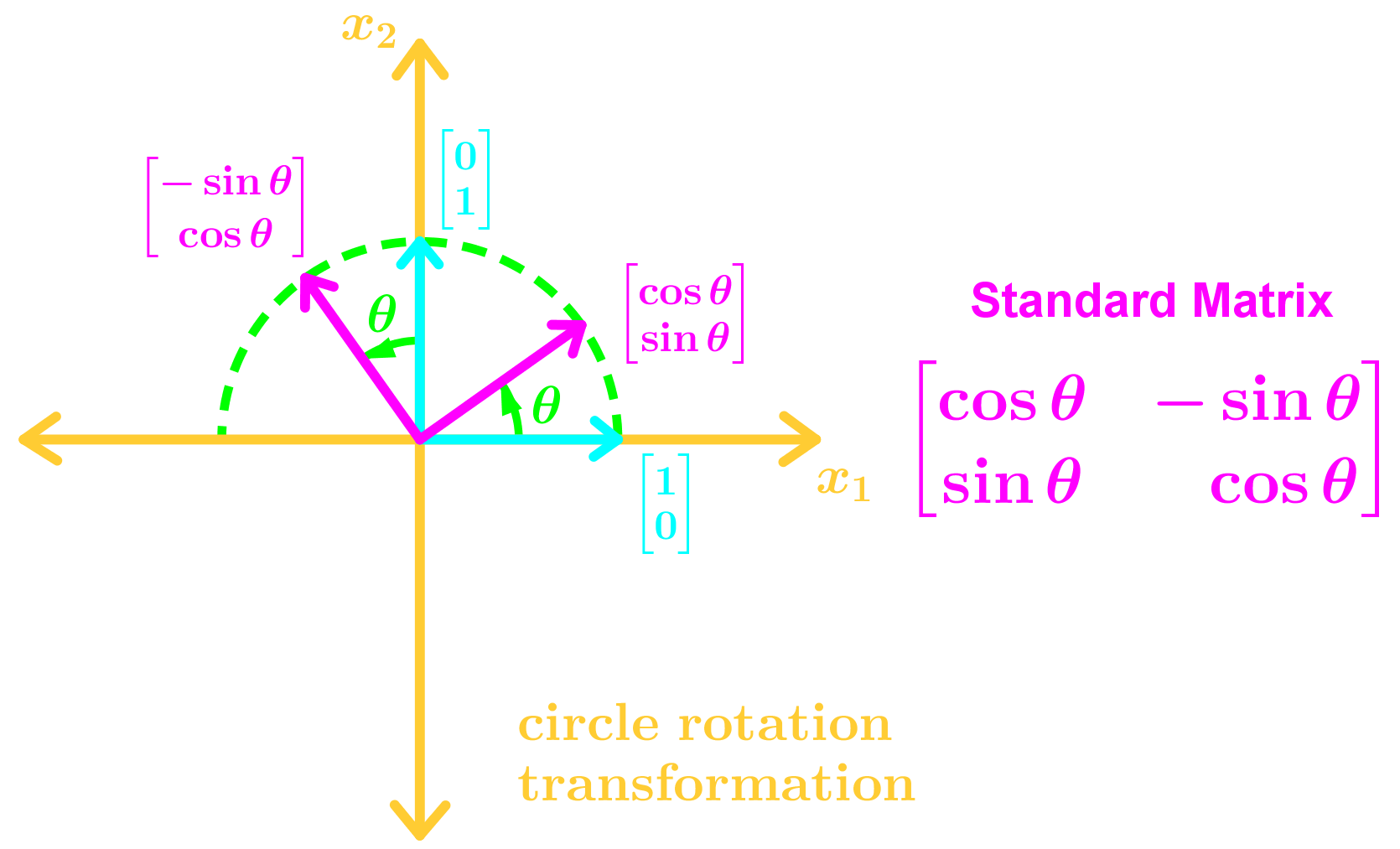
Rotation Matrix Standard Basis . A rotation matrix can be defined as a transformation matrix that is used to rotate a vector in euclidean space. The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. Suppose that ↵ 2 r. Any vector in the plane can be written in polar coordinates as r(cos( ), sin( )) where r 0 and 2 r. Be the function defined as follows: The vector is conventionally rotated in the counterclockwise direction by. To calculate the rotation matrix, with reference to the standard basis, it suffices to consider what are the transformed vectors for.
from www.studypug.com
Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. To calculate the rotation matrix, with reference to the standard basis, it suffices to consider what are the transformed vectors for. Suppose that ↵ 2 r. The vector is conventionally rotated in the counterclockwise direction by. The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. Be the function defined as follows: Any vector in the plane can be written in polar coordinates as r(cos( ), sin( )) where r 0 and 2 r. A rotation matrix can be defined as a transformation matrix that is used to rotate a vector in euclidean space.
Find the Standard Matrix of a Linear Transformation StudyPug
Rotation Matrix Standard Basis Be the function defined as follows: Be the function defined as follows: The vector is conventionally rotated in the counterclockwise direction by. The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. Suppose that ↵ 2 r. To calculate the rotation matrix, with reference to the standard basis, it suffices to consider what are the transformed vectors for. Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. Any vector in the plane can be written in polar coordinates as r(cos( ), sin( )) where r 0 and 2 r. A rotation matrix can be defined as a transformation matrix that is used to rotate a vector in euclidean space.
From www.mauriciopoppe.com
Transformation matrix Mauricio Poppe Rotation Matrix Standard Basis A rotation matrix can be defined as a transformation matrix that is used to rotate a vector in euclidean space. Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. Be the function defined as follows: Suppose that ↵ 2 r. Any vector in the plane can be written in polar coordinates as. Rotation Matrix Standard Basis.
From austinmorlan.com
Deriving the 3D Rotation Matrix Austin Morlan Rotation Matrix Standard Basis Be the function defined as follows: To calculate the rotation matrix, with reference to the standard basis, it suffices to consider what are the transformed vectors for. Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. Suppose that ↵ 2 r. A rotation matrix can be defined as a transformation matrix that. Rotation Matrix Standard Basis.
From www.slideserve.com
PPT CSCE 590E Spring 2007 PowerPoint Presentation, free download ID Rotation Matrix Standard Basis The vector is conventionally rotated in the counterclockwise direction by. The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. To calculate the rotation matrix, with reference to the standard basis, it suffices to consider what are the transformed vectors for. Suppose that ↵ 2 r.. Rotation Matrix Standard Basis.
From 9to5answer.com
[Solved] How to find the rotation matrix between two 9to5Answer Rotation Matrix Standard Basis The vector is conventionally rotated in the counterclockwise direction by. A rotation matrix can be defined as a transformation matrix that is used to rotate a vector in euclidean space. Be the function defined as follows: Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. To calculate the rotation matrix, with reference. Rotation Matrix Standard Basis.
From www.youtube.com
Rotation Matrix for 2D Vectors YouTube Rotation Matrix Standard Basis The vector is conventionally rotated in the counterclockwise direction by. Any vector in the plane can be written in polar coordinates as r(cos( ), sin( )) where r 0 and 2 r. Suppose that ↵ 2 r. Be the function defined as follows: A rotation matrix can be defined as a transformation matrix that is used to rotate a vector. Rotation Matrix Standard Basis.
From www.chegg.com
Solved Implement and test the below 3D rotation matrix in Rotation Matrix Standard Basis To calculate the rotation matrix, with reference to the standard basis, it suffices to consider what are the transformed vectors for. Suppose that ↵ 2 r. The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. A rotation matrix can be defined as a transformation matrix. Rotation Matrix Standard Basis.
From www.youtube.com
2.2 Rotation Matrices YouTube Rotation Matrix Standard Basis The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. Be the function defined as follows: Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. The vector is conventionally rotated in the counterclockwise direction by. Any vector in. Rotation Matrix Standard Basis.
From www.researchgate.net
Definition of the rotation matrices trough the axis x, y and z (taken Rotation Matrix Standard Basis A rotation matrix can be defined as a transformation matrix that is used to rotate a vector in euclidean space. Be the function defined as follows: The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. The vector is conventionally rotated in the counterclockwise direction by.. Rotation Matrix Standard Basis.
From www.youtube.com
Rotating a Vector with the Rotation Matrix YouTube Rotation Matrix Standard Basis Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. Suppose that ↵ 2 r. Any vector in the plane can be written in polar coordinates as r(cos( ),. Rotation Matrix Standard Basis.
From stackoverflow.com
math Understanding rotation matrices derivation Stack Overflow Rotation Matrix Standard Basis Suppose that ↵ 2 r. Any vector in the plane can be written in polar coordinates as r(cos( ), sin( )) where r 0 and 2 r. A rotation matrix can be defined as a transformation matrix that is used to rotate a vector in euclidean space. The most general rotation matrix represents a counterclockwise rotation by an angle θ. Rotation Matrix Standard Basis.
From www.mathworks.com
Rotation matrix for rotations around zaxis MATLAB rotz Rotation Matrix Standard Basis Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. The vector is conventionally rotated in the counterclockwise direction by. The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. To calculate the rotation matrix, with reference to the. Rotation Matrix Standard Basis.
From www.pinterest.com
Rotation Matrix Interactive 3D Graphics YouTube Interactive Rotation Matrix Standard Basis A rotation matrix can be defined as a transformation matrix that is used to rotate a vector in euclidean space. Suppose that ↵ 2 r. The vector is conventionally rotated in the counterclockwise direction by. The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. To. Rotation Matrix Standard Basis.
From www.coursehero.com
[Solved] . Determine the rotation matrix for the following rotation of Rotation Matrix Standard Basis The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. A rotation matrix can be defined as a transformation matrix that is used to rotate a vector in euclidean space. Suppose that ↵ 2 r. To calculate the rotation matrix, with reference to the standard basis,. Rotation Matrix Standard Basis.
From www.numerade.com
SOLVED Calculate the 3x3 rotation matrices that perform a rotation of Rotation Matrix Standard Basis Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. The vector is conventionally rotated in the counterclockwise direction by. Be the function defined as follows: A rotation matrix can be defined as a transformation matrix that is used to rotate a vector in euclidean space. Suppose that ↵ 2 r. Any vector. Rotation Matrix Standard Basis.
From www.slideserve.com
PPT Transformations PowerPoint Presentation, free download ID5550000 Rotation Matrix Standard Basis Suppose that ↵ 2 r. The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. A rotation matrix can be defined as a transformation matrix that is used to rotate a vector in euclidean space. Counterclockwise rotation about the origin by (in radians) is a linear. Rotation Matrix Standard Basis.
From www.studypug.com
Find the Standard Matrix of a Linear Transformation StudyPug Rotation Matrix Standard Basis To calculate the rotation matrix, with reference to the standard basis, it suffices to consider what are the transformed vectors for. Any vector in the plane can be written in polar coordinates as r(cos( ), sin( )) where r 0 and 2 r. The vector is conventionally rotated in the counterclockwise direction by. Counterclockwise rotation about the origin by (in. Rotation Matrix Standard Basis.
From slideplayer.com
Rotations and Quaternions Week 9, Wed 29 Oct ppt download Rotation Matrix Standard Basis To calculate the rotation matrix, with reference to the standard basis, it suffices to consider what are the transformed vectors for. Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. The vector is conventionally rotated in the counterclockwise direction by. A rotation matrix can be defined as a transformation matrix that is. Rotation Matrix Standard Basis.
From www.youtube.com
90 Degree Clockwise Rotation Transformation Matrix YouTube Rotation Matrix Standard Basis A rotation matrix can be defined as a transformation matrix that is used to rotate a vector in euclidean space. To calculate the rotation matrix, with reference to the standard basis, it suffices to consider what are the transformed vectors for. Any vector in the plane can be written in polar coordinates as r(cos( ), sin( )) where r 0. Rotation Matrix Standard Basis.
From www.slideserve.com
PPT Reminder PowerPoint Presentation ID3643947 Rotation Matrix Standard Basis Suppose that ↵ 2 r. Any vector in the plane can be written in polar coordinates as r(cos( ), sin( )) where r 0 and 2 r. The vector is conventionally rotated in the counterclockwise direction by. Be the function defined as follows: The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis. Rotation Matrix Standard Basis.
From www.chegg.com
2) [25pts] The derivation for rotation matrices and Rotation Matrix Standard Basis The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. The vector is conventionally rotated in the counterclockwise direction by. A rotation matrix can be defined as a transformation matrix that is used to rotate a vector in euclidean space. Counterclockwise rotation about the origin by. Rotation Matrix Standard Basis.
From www.youtube.com
Rotation Matrix for Coordinate Transformation YouTube Rotation Matrix Standard Basis Be the function defined as follows: Any vector in the plane can be written in polar coordinates as r(cos( ), sin( )) where r 0 and 2 r. Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. Suppose that ↵ 2 r. To calculate the rotation matrix, with reference to the standard. Rotation Matrix Standard Basis.
From www.youtube.com
2014W ENGR486 Lecture02 Basic Rotation Matrix YouTube Rotation Matrix Standard Basis The vector is conventionally rotated in the counterclockwise direction by. Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. Be the function defined as follows: The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. Any vector in. Rotation Matrix Standard Basis.
From www.chegg.com
Solved 1. Determine if the following rotation matrices are Rotation Matrix Standard Basis Any vector in the plane can be written in polar coordinates as r(cos( ), sin( )) where r 0 and 2 r. The vector is conventionally rotated in the counterclockwise direction by. Be the function defined as follows: Suppose that ↵ 2 r. To calculate the rotation matrix, with reference to the standard basis, it suffices to consider what are. Rotation Matrix Standard Basis.
From austinmorlan.com
Deriving the 3D Rotation Matrix Austin Morlan Rotation Matrix Standard Basis Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. Any vector in the plane can be written in polar coordinates as r(cos( ), sin( )) where r 0 and 2 r. Suppose that ↵ 2 r. A rotation matrix can be defined as a transformation matrix that is used to rotate a. Rotation Matrix Standard Basis.
From www.coursehero.com
[Solved] . Determine the rotation matrix for the following rotation of Rotation Matrix Standard Basis The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. The vector is conventionally rotated in the counterclockwise direction by. Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. Any vector in the plane can be written in. Rotation Matrix Standard Basis.
From www.youtube.com
Rotate Matrix by 90 degrees clockwise Rotate Image YouTube Rotation Matrix Standard Basis To calculate the rotation matrix, with reference to the standard basis, it suffices to consider what are the transformed vectors for. Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. Be the function defined as follows: Any vector in the plane can be written in polar coordinates as r(cos( ), sin( )). Rotation Matrix Standard Basis.
From www.slideserve.com
PPT Manipulation PowerPoint Presentation, free download ID1869278 Rotation Matrix Standard Basis Suppose that ↵ 2 r. The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. The vector is conventionally rotated in the counterclockwise direction by. Any vector in the plane can be written in polar coordinates as r(cos( ), sin( )) where r 0 and 2. Rotation Matrix Standard Basis.
From allinpython.com
Rotate a Matrix by 90 Degrees in python with User input Rotation Matrix Standard Basis A rotation matrix can be defined as a transformation matrix that is used to rotate a vector in euclidean space. The vector is conventionally rotated in the counterclockwise direction by. Be the function defined as follows: Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. Suppose that ↵ 2 r. Any vector. Rotation Matrix Standard Basis.
From www.slideserve.com
PPT Transformations PowerPoint Presentation, free download ID5550000 Rotation Matrix Standard Basis A rotation matrix can be defined as a transformation matrix that is used to rotate a vector in euclidean space. The vector is conventionally rotated in the counterclockwise direction by. Be the function defined as follows: Any vector in the plane can be written in polar coordinates as r(cos( ), sin( )) where r 0 and 2 r. Suppose that. Rotation Matrix Standard Basis.
From www.youtube.com
Chapter 2 Rotation of basis states and matrix mechanics YouTube Rotation Matrix Standard Basis A rotation matrix can be defined as a transformation matrix that is used to rotate a vector in euclidean space. Be the function defined as follows: The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. Counterclockwise rotation about the origin by (in radians) is a. Rotation Matrix Standard Basis.
From www.i-ciencias.com
[Solucionado] Entender las matrices de rotación álgebralineal Rotation Matrix Standard Basis The vector is conventionally rotated in the counterclockwise direction by. Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. A rotation matrix can be defined as a transformation. Rotation Matrix Standard Basis.
From www.mathaddict.net
3D Rotational Matrix Rotation Matrix Standard Basis Be the function defined as follows: To calculate the rotation matrix, with reference to the standard basis, it suffices to consider what are the transformed vectors for. The vector is conventionally rotated in the counterclockwise direction by. Any vector in the plane can be written in polar coordinates as r(cos( ), sin( )) where r 0 and 2 r. The. Rotation Matrix Standard Basis.
From www.slideserve.com
PPT Lecture 1 PowerPoint Presentation, free download ID4004577 Rotation Matrix Standard Basis The most general rotation matrix represents a counterclockwise rotation by an angle θ about a fixed axis that lies along the unit vector ˆn. Any vector in the plane can be written in polar coordinates as r(cos( ), sin( )) where r 0 and 2 r. Suppose that ↵ 2 r. To calculate the rotation matrix, with reference to the. Rotation Matrix Standard Basis.
From www.youtube.com
Linear Transformation Combination of CCW 90 Rotation and Reflection on Rotation Matrix Standard Basis To calculate the rotation matrix, with reference to the standard basis, it suffices to consider what are the transformed vectors for. Be the function defined as follows: Any vector in the plane can be written in polar coordinates as r(cos( ), sin( )) where r 0 and 2 r. Counterclockwise rotation about the origin by (in radians) is a linear. Rotation Matrix Standard Basis.
From www.slideserve.com
PPT Vectors, Matrices, Rotations Spring 2005 PowerPoint Presentation Rotation Matrix Standard Basis Suppose that ↵ 2 r. Counterclockwise rotation about the origin by (in radians) is a linear transformation, and its standard matrix is. The vector is conventionally rotated in the counterclockwise direction by. To calculate the rotation matrix, with reference to the standard basis, it suffices to consider what are the transformed vectors for. Be the function defined as follows: The. Rotation Matrix Standard Basis.