Continuous Piecewise Linear Functions . This kind of approximation to a curve is known as. See examples, domain and range, and piecewise. some piecewise functions are continuous like the one depicted above, whereas some are not continuous. to determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous apart from a set of isolated points. a typical use of continuous piecewise linear functions is when we link several points in a graph using segments. — learn what a piecewise linear function is and how to approximate it with increasing number of segments. learn how to graph piecewise functions with multiple definitions and different pieces of curves.
from www.onlinemathlearning.com
some piecewise functions are continuous like the one depicted above, whereas some are not continuous. learn how to graph piecewise functions with multiple definitions and different pieces of curves. — learn what a piecewise linear function is and how to approximate it with increasing number of segments. See examples, domain and range, and piecewise. This kind of approximation to a curve is known as. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous apart from a set of isolated points. to determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each. a typical use of continuous piecewise linear functions is when we link several points in a graph using segments.
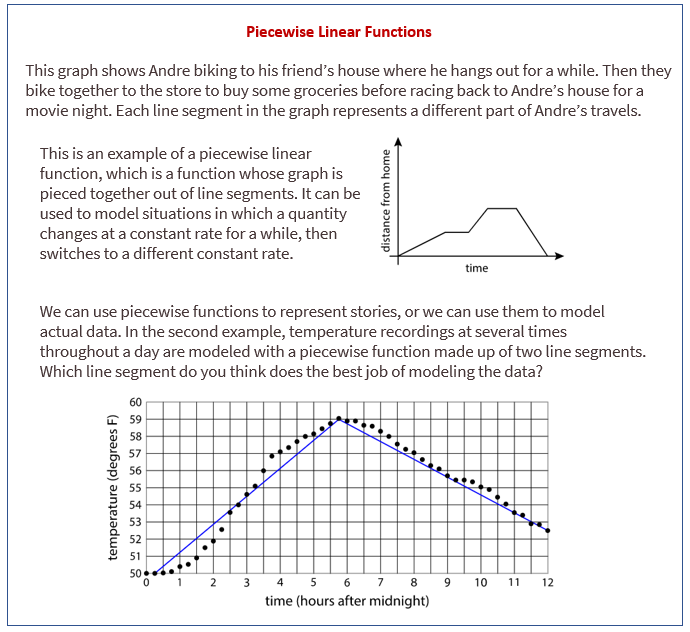
Piecewise Linear Functions
Continuous Piecewise Linear Functions to determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each. — learn what a piecewise linear function is and how to approximate it with increasing number of segments. See examples, domain and range, and piecewise. This kind of approximation to a curve is known as. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous apart from a set of isolated points. learn how to graph piecewise functions with multiple definitions and different pieces of curves. a typical use of continuous piecewise linear functions is when we link several points in a graph using segments. some piecewise functions are continuous like the one depicted above, whereas some are not continuous. to determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each.
From ihsanpedia.com
How To Graph Functions A Comprehensive Guide IHSANPEDIA Continuous Piecewise Linear Functions This kind of approximation to a curve is known as. — learn what a piecewise linear function is and how to approximate it with increasing number of segments. See examples, domain and range, and piecewise. a typical use of continuous piecewise linear functions is when we link several points in a graph using segments. to determine whether. Continuous Piecewise Linear Functions.
From www.youtube.com
Piecewise Functions YouTube Continuous Piecewise Linear Functions This kind of approximation to a curve is known as. learn how to graph piecewise functions with multiple definitions and different pieces of curves. to determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each. — learn what a piecewise linear function is and how. Continuous Piecewise Linear Functions.
From www.youtube.com
10.5 Example 2 Graphing Piecewise Linear Functions YouTube Continuous Piecewise Linear Functions — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous apart from a set of isolated points. learn how to graph piecewise functions with multiple definitions and different pieces of curves. — learn what a piecewise linear function is and how to approximate it with increasing number of segments. to. Continuous Piecewise Linear Functions.
From www.nagwa.com
Lesson Video Graphs of Piecewise Functions Nagwa Continuous Piecewise Linear Functions a typical use of continuous piecewise linear functions is when we link several points in a graph using segments. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous apart from a set of isolated points. See examples, domain and range, and piecewise. — learn what a piecewise linear function is. Continuous Piecewise Linear Functions.
From www.cuemath.com
Piecewise Function How to Graph? Examples, Evaluating Continuous Piecewise Linear Functions some piecewise functions are continuous like the one depicted above, whereas some are not continuous. a typical use of continuous piecewise linear functions is when we link several points in a graph using segments. See examples, domain and range, and piecewise. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous. Continuous Piecewise Linear Functions.
From www.chegg.com
Solved Consider the continuous, piecewise linear Continuous Piecewise Linear Functions This kind of approximation to a curve is known as. See examples, domain and range, and piecewise. learn how to graph piecewise functions with multiple definitions and different pieces of curves. some piecewise functions are continuous like the one depicted above, whereas some are not continuous. to determine whether a piecewise function is continuous or discontinuous, in. Continuous Piecewise Linear Functions.
From songhuiming.github.io
piecewise linear function and the explanation — pydata Continuous Piecewise Linear Functions This kind of approximation to a curve is known as. some piecewise functions are continuous like the one depicted above, whereas some are not continuous. to determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each. See examples, domain and range, and piecewise. — learn. Continuous Piecewise Linear Functions.
From www.youtube.com
Piecewise Linear Functions YouTube Continuous Piecewise Linear Functions learn how to graph piecewise functions with multiple definitions and different pieces of curves. See examples, domain and range, and piecewise. to determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if. Continuous Piecewise Linear Functions.
From mathbitsnotebook.com
Piecewise, Absolute Value and Step Functions MathBitsNotebook(A2 Continuous Piecewise Linear Functions learn how to graph piecewise functions with multiple definitions and different pieces of curves. This kind of approximation to a curve is known as. a typical use of continuous piecewise linear functions is when we link several points in a graph using segments. — learn what a piecewise linear function is and how to approximate it with. Continuous Piecewise Linear Functions.
From www.researchgate.net
(PDF) Learning of Continuous and PiecewiseLinear Functions With Continuous Piecewise Linear Functions some piecewise functions are continuous like the one depicted above, whereas some are not continuous. a typical use of continuous piecewise linear functions is when we link several points in a graph using segments. See examples, domain and range, and piecewise. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous. Continuous Piecewise Linear Functions.
From hra.animalia-life.club
Linear Piecewise Graph Continuous Piecewise Linear Functions — learn what a piecewise linear function is and how to approximate it with increasing number of segments. learn how to graph piecewise functions with multiple definitions and different pieces of curves. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous apart from a set of isolated points. a. Continuous Piecewise Linear Functions.
From www.shelovesmath.com
Piecewise Functions She Loves Math Continuous Piecewise Linear Functions learn how to graph piecewise functions with multiple definitions and different pieces of curves. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous apart from a set of isolated points. — learn what a piecewise linear function is and how to approximate it with increasing number of segments. to. Continuous Piecewise Linear Functions.
From www.slideserve.com
PPT Graphs of Piecewise Linear Functions PowerPoint Presentation Continuous Piecewise Linear Functions some piecewise functions are continuous like the one depicted above, whereas some are not continuous. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous apart from a set of isolated points. learn how to graph piecewise functions with multiple definitions and different pieces of curves. to determine whether a. Continuous Piecewise Linear Functions.
From www.researchgate.net
Example of fitting a continuous piecewise linear function with Continuous Piecewise Linear Functions a typical use of continuous piecewise linear functions is when we link several points in a graph using segments. some piecewise functions are continuous like the one depicted above, whereas some are not continuous. — learn what a piecewise linear function is and how to approximate it with increasing number of segments. See examples, domain and range,. Continuous Piecewise Linear Functions.
From www.cuemath.com
Piecewise Function How to Graph? Examples, Evaluating Continuous Piecewise Linear Functions — learn what a piecewise linear function is and how to approximate it with increasing number of segments. See examples, domain and range, and piecewise. This kind of approximation to a curve is known as. learn how to graph piecewise functions with multiple definitions and different pieces of curves. to determine whether a piecewise function is continuous. Continuous Piecewise Linear Functions.
From www.youtube.com
Plot piecewise continuous function with MATLAB? Plot piecewise Continuous Piecewise Linear Functions some piecewise functions are continuous like the one depicted above, whereas some are not continuous. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous apart from a set of isolated points. to determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must. Continuous Piecewise Linear Functions.
From www.youtube.com
Graphing a PiecewiseDefined Function Example 8 YouTube Continuous Piecewise Linear Functions learn how to graph piecewise functions with multiple definitions and different pieces of curves. a typical use of continuous piecewise linear functions is when we link several points in a graph using segments. to determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each. . Continuous Piecewise Linear Functions.
From www.researchgate.net
Schematic of the piecewise linear rate functions. The piecewise linear Continuous Piecewise Linear Functions some piecewise functions are continuous like the one depicted above, whereas some are not continuous. This kind of approximation to a curve is known as. to determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each. learn how to graph piecewise functions with multiple definitions. Continuous Piecewise Linear Functions.
From www.researchgate.net
6 A continuous piecewise linear function in V h . Download Continuous Piecewise Linear Functions See examples, domain and range, and piecewise. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous apart from a set of isolated points. This kind of approximation to a curve is known as. learn how to graph piecewise functions with multiple definitions and different pieces of curves. — learn what. Continuous Piecewise Linear Functions.
From www.youtube.com
Determine if the Piecewise Function is Continuous by using the Continuous Piecewise Linear Functions to determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each. some piecewise functions are continuous like the one depicted above, whereas some are not continuous. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous apart from a. Continuous Piecewise Linear Functions.
From www.youtube.com
Piecewise Functions YouTube Continuous Piecewise Linear Functions a typical use of continuous piecewise linear functions is when we link several points in a graph using segments. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous apart from a set of isolated points. some piecewise functions are continuous like the one depicted above, whereas some are not continuous.. Continuous Piecewise Linear Functions.
From www.kristakingmath.com
Modeling a piecewisedefined function from its graph — Krista King Math Continuous Piecewise Linear Functions — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous apart from a set of isolated points. This kind of approximation to a curve is known as. a typical use of continuous piecewise linear functions is when we link several points in a graph using segments. learn how to graph piecewise. Continuous Piecewise Linear Functions.
From www.chegg.com
Solved Consider the sequence of continuous piecewise linear Continuous Piecewise Linear Functions — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous apart from a set of isolated points. — learn what a piecewise linear function is and how to approximate it with increasing number of segments. a typical use of continuous piecewise linear functions is when we link several points in a. Continuous Piecewise Linear Functions.
From mszeilstra.weebly.com
2.7 Piecewise Functions Ms. Zeilstra's Math Classes Continuous Piecewise Linear Functions a typical use of continuous piecewise linear functions is when we link several points in a graph using segments. See examples, domain and range, and piecewise. to determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each. — a function $f$ is piecewise continuous on. Continuous Piecewise Linear Functions.
From www.youtube.com
Graphing Piecewise Functions Linear Models YouTube Continuous Piecewise Linear Functions See examples, domain and range, and piecewise. learn how to graph piecewise functions with multiple definitions and different pieces of curves. to determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each. some piecewise functions are continuous like the one depicted above, whereas some are. Continuous Piecewise Linear Functions.
From studylib.net
Worksheet Piecewise Functions Continuous Piecewise Linear Functions some piecewise functions are continuous like the one depicted above, whereas some are not continuous. — learn what a piecewise linear function is and how to approximate it with increasing number of segments. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous apart from a set of isolated points. This. Continuous Piecewise Linear Functions.
From wikihow.com
How to Graph a Piecewise Function 7 Steps (with Pictures) Continuous Piecewise Linear Functions See examples, domain and range, and piecewise. This kind of approximation to a curve is known as. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous apart from a set of isolated points. learn how to graph piecewise functions with multiple definitions and different pieces of curves. some piecewise functions. Continuous Piecewise Linear Functions.
From www.youtube.com
How to make a function continuous (for a piecewise function Continuous Piecewise Linear Functions See examples, domain and range, and piecewise. This kind of approximation to a curve is known as. learn how to graph piecewise functions with multiple definitions and different pieces of curves. some piecewise functions are continuous like the one depicted above, whereas some are not continuous. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb. Continuous Piecewise Linear Functions.
From brilliant.org
Piecewise Functions Brilliant Math & Science Wiki Continuous Piecewise Linear Functions learn how to graph piecewise functions with multiple definitions and different pieces of curves. some piecewise functions are continuous like the one depicted above, whereas some are not continuous. to determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each. See examples, domain and range,. Continuous Piecewise Linear Functions.
From betterlesson.com
Ninth grade Lesson Writing, Graphing, and Describing Piecewise Linear Continuous Piecewise Linear Functions learn how to graph piecewise functions with multiple definitions and different pieces of curves. to determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each. See examples, domain and range, and piecewise. This kind of approximation to a curve is known as. a typical use. Continuous Piecewise Linear Functions.
From answerlisthydra.z21.web.core.windows.net
How To Solve Piecewise Functions With Graph Continuous Piecewise Linear Functions a typical use of continuous piecewise linear functions is when we link several points in a graph using segments. to determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each. See examples, domain and range, and piecewise. learn how to graph piecewise functions with multiple. Continuous Piecewise Linear Functions.
From studylib.net
PIECEWISE FUNCTIONS Continuous Piecewise Linear Functions to determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each. — learn what a piecewise linear function is and how to approximate it with increasing number of segments. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous. Continuous Piecewise Linear Functions.
From www.onlinemathlearning.com
Piecewise Linear Functions Continuous Piecewise Linear Functions learn how to graph piecewise functions with multiple definitions and different pieces of curves. a typical use of continuous piecewise linear functions is when we link several points in a graph using segments. — learn what a piecewise linear function is and how to approximate it with increasing number of segments. This kind of approximation to a. Continuous Piecewise Linear Functions.
From file.scirp.org
Continuous Piecewise Linear Approximation of BV Function Continuous Piecewise Linear Functions — learn what a piecewise linear function is and how to approximate it with increasing number of segments. This kind of approximation to a curve is known as. a typical use of continuous piecewise linear functions is when we link several points in a graph using segments. learn how to graph piecewise functions with multiple definitions and. Continuous Piecewise Linear Functions.
From www.chegg.com
Consider the continuous piecewise linear function F Continuous Piecewise Linear Functions to determine whether a piecewise function is continuous or discontinuous, in addition to checking the boundary points, we must also check whether each. — a function $f$ is piecewise continuous on an interval $j\subset{\mathbb r}$ if it is continuous apart from a set of isolated points. a typical use of continuous piecewise linear functions is when we. Continuous Piecewise Linear Functions.