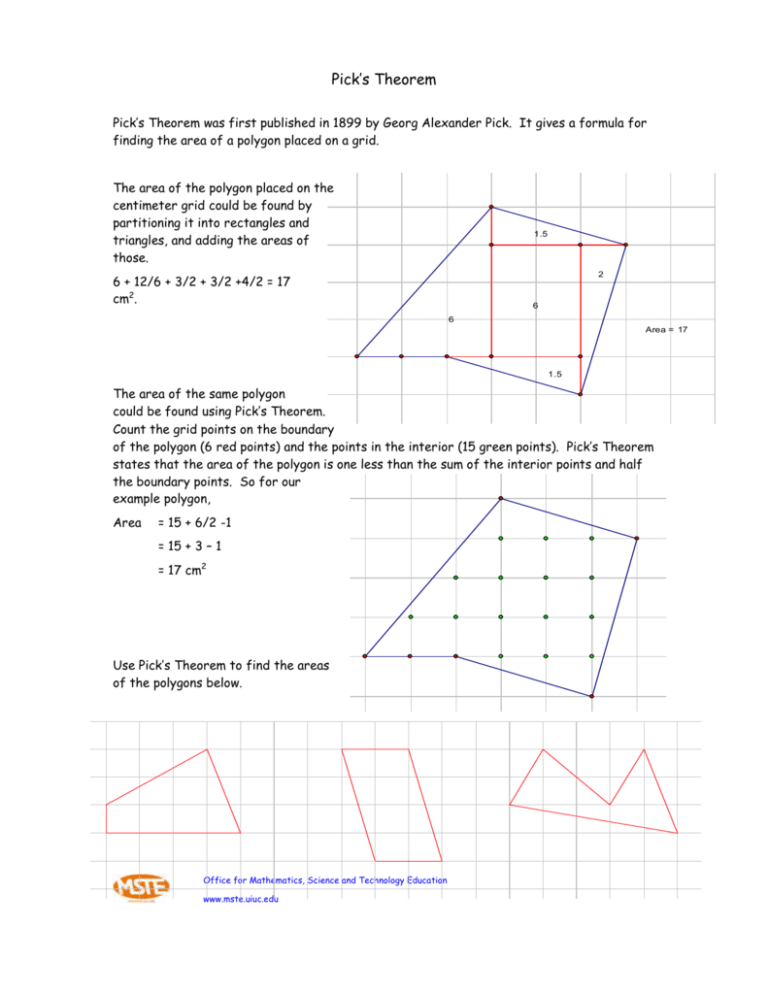
Pick's Theorem Equation . Pick's theorem says the area of a lattice polygon is the number of interior points plus half the number of lattice points on the. The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Let a be the area of a simply closed lattice polygon. Pick's theorem gives a way to find the area of a lattice polygon without performing all of these calculations. Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. Pick's theorem also implies the. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the. Let b denote the number of lattice points on the polygon edges and i the number of.
from studylib.net
The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. Let b denote the number of lattice points on the polygon edges and i the number of. Pick's theorem also implies the. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the. Pick's theorem says the area of a lattice polygon is the number of interior points plus half the number of lattice points on the. Let a be the area of a simply closed lattice polygon. Pick's theorem gives a way to find the area of a lattice polygon without performing all of these calculations.
Pick`s Theorem Office for Mathematics, Science, and Technology
Pick's Theorem Equation Let b denote the number of lattice points on the polygon edges and i the number of. Pick's theorem gives a way to find the area of a lattice polygon without performing all of these calculations. The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Pick's theorem says the area of a lattice polygon is the number of interior points plus half the number of lattice points on the. Pick's theorem also implies the. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the. Let a be the area of a simply closed lattice polygon. Let b denote the number of lattice points on the polygon edges and i the number of. Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well.
From fr.mathigon.org
Pick’s Theorem Mathigon Pick's Theorem Equation Pick's theorem also implies the. Pick's theorem gives a way to find the area of a lattice polygon without performing all of these calculations. Let b denote the number of lattice points on the polygon edges and i the number of. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane,. Pick's Theorem Equation.
From www.scribd.com
Pick's Theorem PDF Pick's Theorem Equation Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. Pick's theorem gives a way to find the area of a lattice polygon without performing all of these calculations. The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the. Pick's Theorem Equation.
From www.geogebra.org
Fórmula de Pick GeoGebra Pick's Theorem Equation The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Let b denote the number of lattice points on the polygon edges and i the number of. Let a be the area of a simply closed lattice polygon. Pick's theorem gives a way. Pick's Theorem Equation.
From hubpages.com
Pick’s Theorem To Find The Area Of A Polygon HubPages Pick's Theorem Equation Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Pick's theorem gives a way to find the area of a lattice polygon without. Pick's Theorem Equation.
From hubpages.com
Pick’s Theorem To Find The Area Of A Polygon HubPages Pick's Theorem Equation Pick's theorem says the area of a lattice polygon is the number of interior points plus half the number of lattice points on the. Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. The area inside the polygon is computed by counting all of the dots fully inside the polygon,. Pick's Theorem Equation.
From yokehiang.blogspot.com
Yoke hiang & Math Pick's Theorem Equation Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. Pick's theorem also implies the. The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Let a be the area of a simply closed. Pick's Theorem Equation.
From pt.slideshare.net
Teorema de pick Pick's Theorem Equation Let b denote the number of lattice points on the polygon edges and i the number of. Pick's theorem also implies the. Pick's theorem gives a way to find the area of a lattice polygon without performing all of these calculations. Pick's theorem says the area of a lattice polygon is the number of interior points plus half the number. Pick's Theorem Equation.
From connect.learnpad.com
Picks Theorem Content ClassConnect Pick's Theorem Equation Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Pick's theorem says the area of a lattice polygon is the number of interior. Pick's Theorem Equation.
From www.youtube.com
Pick's Theorem (From Euler's Planar Graph Formula) YouTube Pick's Theorem Equation Pick's theorem gives a way to find the area of a lattice polygon without performing all of these calculations. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the. The area inside the polygon is computed by counting all of the dots fully inside the polygon, and. Pick's Theorem Equation.
From studylib.net
Pick`s Theorem Pick's Theorem Equation Let b denote the number of lattice points on the polygon edges and i the number of. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the. Pick's theorem gives a way to find the area of a lattice polygon without performing all of these calculations. Pick's. Pick's Theorem Equation.
From catalogue-staging.cpcompany.com
Teorema De Pick Fórmula BRAINCP Pick's Theorem Equation The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the. Pick's theorem also implies the. Pick's theorem gives a way. Pick's Theorem Equation.
From discover.hubpages.com
Pick’s Theorem To Find The Area Of A Polygon HubPages Pick's Theorem Equation Pick's theorem also implies the. The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Pick's theorem says the area of a lattice polygon is the number of interior points plus half the number of lattice points on the. Polygons drawn on square. Pick's Theorem Equation.
From www.studypool.com
SOLUTION Pick's theorem (presentation) Studypool Pick's Theorem Equation The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Pick's theorem gives a way to find the area of a lattice polygon without performing all of these calculations. Pick's theorem also implies the. Let b denote the number of lattice points on. Pick's Theorem Equation.
From www.geogebra.org
Pick's Theorem Explorer GeoGebra Pick's Theorem Equation Pick's theorem gives a way to find the area of a lattice polygon without performing all of these calculations. Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of. Pick's Theorem Equation.
From studylib.net
Pick`s Theorem Office for Mathematics, Science, and Technology Pick's Theorem Equation Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. Let a be the area of a simply closed lattice polygon. The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Pick's theorem also. Pick's Theorem Equation.
From www.lessonplanet.com
Proving Pick's Theorem Instructional Video for 10th Higher Ed Pick's Theorem Equation The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice. Pick's Theorem Equation.
From www.youtube.com
Pick's Theorem How to Work Out the Area of a Polygon Just by Counting Pick's Theorem Equation The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Let a be the area of a simply closed lattice polygon. Pick's theorem gives a way to find the area of a lattice polygon without performing all of these calculations. Polygons drawn on. Pick's Theorem Equation.
From hr.mathigon.org
Pick’s Theorem Mathigon Pick's Theorem Equation Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the. Let b denote the number of lattice points on the polygon edges and i the number of. The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half. Pick's Theorem Equation.
From www.studypool.com
SOLUTION Pick's theorem (presentation) Studypool Pick's Theorem Equation Pick's theorem says the area of a lattice polygon is the number of interior points plus half the number of lattice points on the. Let a be the area of a simply closed lattice polygon. Pick's theorem gives a way to find the area of a lattice polygon without performing all of these calculations. Pick's theorem expresses the area of. Pick's Theorem Equation.
From www.youtube.com
Pick's Theorem YouTube Pick's Theorem Equation Let a be the area of a simply closed lattice polygon. Pick's theorem says the area of a lattice polygon is the number of interior points plus half the number of lattice points on the. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the. Polygons drawn. Pick's Theorem Equation.
From www.teachit.co.uk
Investigating area using Pick's theorem KS34 maths Teachit Pick's Theorem Equation Let a be the area of a simply closed lattice polygon. The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Pick's theorem says the area of a lattice polygon is the number of interior points plus half the number of lattice points. Pick's Theorem Equation.
From www.geogebra.org
Lesson Pick's Theorem GeoGebra Pick's Theorem Equation Let a be the area of a simply closed lattice polygon. Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. Pick's theorem gives a way to find the area of a lattice polygon without performing all of these calculations. Pick's theorem says the area of a lattice polygon is the. Pick's Theorem Equation.
From www.youtube.com
Pick's Theorem to find the Area of Green Polygon instantly Important Pick's Theorem Equation The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Let b denote the number of lattice points on the polygon edges and i the number of. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in. Pick's Theorem Equation.
From en.etudes.ru
Pick’s formula / Etudes // Mathematical Etudes Pick's Theorem Equation The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the. Let b denote the number of lattice points on the. Pick's Theorem Equation.
From hubpages.com
Pick’s Theorem To Find The Area Of A Polygon HubPages Pick's Theorem Equation Let b denote the number of lattice points on the polygon edges and i the number of. The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in. Pick's Theorem Equation.
From studylib.net
Pick’s Theorem Examples Tom Davis Part I Pick's Theorem Equation Pick's theorem gives a way to find the area of a lattice polygon without performing all of these calculations. Pick's theorem also implies the. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the. Polygons drawn on square dotty paper have dots on their perimeter (p) and. Pick's Theorem Equation.
From www.slideserve.com
PPT Applications of Euler’s Formula for Graphs PowerPoint Pick's Theorem Equation Pick's theorem says the area of a lattice polygon is the number of interior points plus half the number of lattice points on the. Pick's theorem gives a way to find the area of a lattice polygon without performing all of these calculations. Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones. Pick's Theorem Equation.
From www.youtube.com
Pick's Theorem YouTube Pick's Theorem Equation The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Let b denote the number of lattice points on the polygon edges and i the number of. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in. Pick's Theorem Equation.
From mathblogpro.blogspot.com
Math Blog Pro Blog 4 Pick's Theorem Pick's Theorem Equation Let b denote the number of lattice points on the polygon edges and i the number of. Let a be the area of a simply closed lattice polygon. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the. Pick's theorem gives a way to find the area. Pick's Theorem Equation.
From www.youtube.com
Pick's Theorem Area, boundary points, and interior points. YouTube Pick's Theorem Equation Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Pick's theorem also implies the. Let a be the area of a simply closed. Pick's Theorem Equation.
From www.slideserve.com
PPT Applications of Euler’s Formula for Graphs PowerPoint Pick's Theorem Equation Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the. The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Pick's theorem gives a way to find the area of. Pick's Theorem Equation.
From www.slideserve.com
PPT Applications of Euler’s Formula for Graphs PowerPoint Pick's Theorem Equation Pick's theorem gives a way to find the area of a lattice polygon without performing all of these calculations. Pick's theorem also implies the. Let b denote the number of lattice points on the polygon edges and i the number of. Pick's theorem says the area of a lattice polygon is the number of interior points plus half the number. Pick's Theorem Equation.
From numbers-theory.blogspot.com
Numbers Theory Pick's Theorem Pick's Theorem Equation Pick's theorem gives a way to find the area of a lattice polygon without performing all of these calculations. Polygons drawn on square dotty paper have dots on their perimeter (p) and often internal (i) ones as well. Pick's theorem also implies the. The area inside the polygon is computed by counting all of the dots fully inside the polygon,. Pick's Theorem Equation.
From www.youtube.com
Pick's Theorem YouTube Pick's Theorem Equation The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half of the number of dots which fall. Pick's theorem says the area of a lattice polygon is the number of interior points plus half the number of lattice points on the. Pick's theorem expresses the area of a polygon, all. Pick's Theorem Equation.
From www.academia.edu
(PDF) A Colorful Proof of Pick’s Theorem Jack Graver Academia.edu Pick's Theorem Equation Let b denote the number of lattice points on the polygon edges and i the number of. Pick's theorem expresses the area of a polygon, all of whose vertices are lattice points in a coordinate plane, in terms of the. The area inside the polygon is computed by counting all of the dots fully inside the polygon, and adding half. Pick's Theorem Equation.