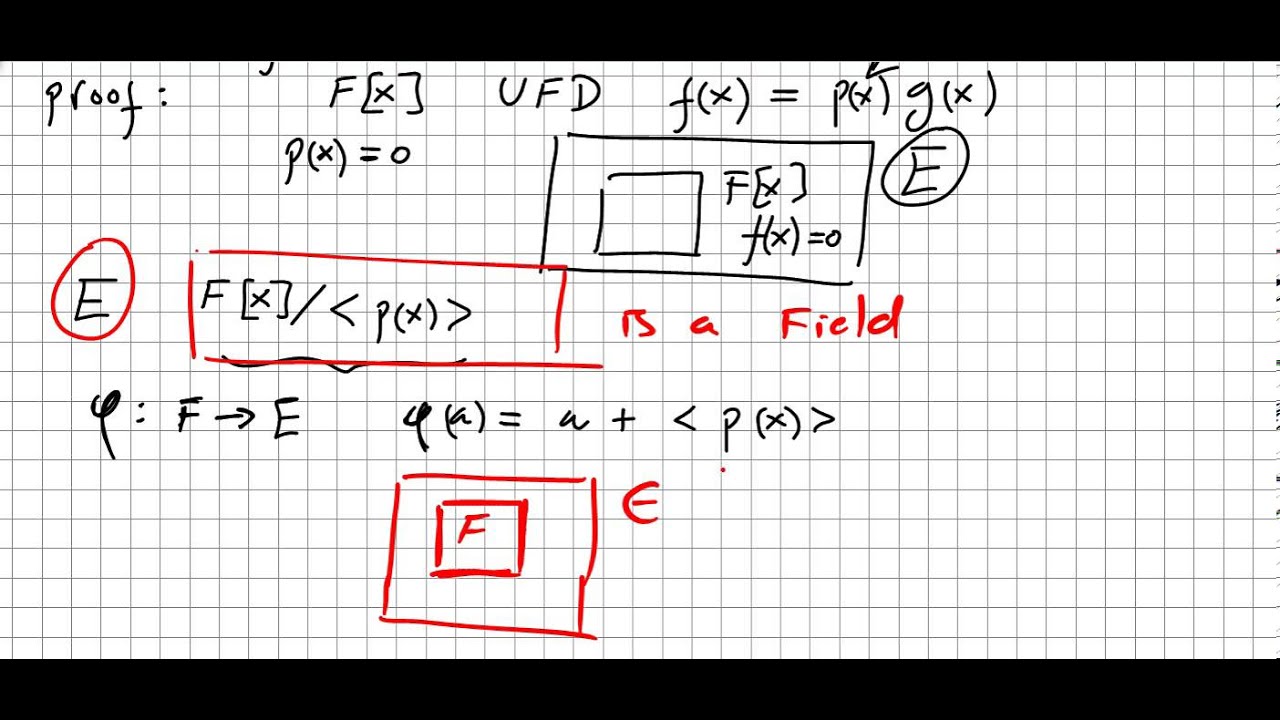
Field Extension With Degree 1 . An extension k/k is called a splitting field for f over k if f splits over k and if l is an intermediate field, say. Let $e/f$ be a finite galois extension, then $$ \varphi: the extension field degree (or relative degree, or index) of an extension field k/f, denoted [k:f], is the dimension of. Every field is a (possibly infinite) extension of either q fp p primary , or for a prime. K \mapsto aut (e/k) $$ and $$ \psi: These are called the fields. degrees of field extensions. olynomial of degree ≥ 1. let \(e\) be an extension field of a field \(f\) and \(\alpha \in e\) with \(\alpha\) algebraic over \(f\text{.}\) then there is a unique. The dimension of this vector space is called the degree of the. Last lecture we introduced the notion of algebraic and transcendental elements over a field, and.
from www.youtube.com
degrees of field extensions. let \(e\) be an extension field of a field \(f\) and \(\alpha \in e\) with \(\alpha\) algebraic over \(f\text{.}\) then there is a unique. Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. the extension field degree (or relative degree, or index) of an extension field k/f, denoted [k:f], is the dimension of. These are called the fields. Let $e/f$ be a finite galois extension, then $$ \varphi: Every field is a (possibly infinite) extension of either q fp p primary , or for a prime. The dimension of this vector space is called the degree of the. An extension k/k is called a splitting field for f over k if f splits over k and if l is an intermediate field, say. K \mapsto aut (e/k) $$ and $$ \psi:
Field Theory 1, Extension Fields YouTube
Field Extension With Degree 1 An extension k/k is called a splitting field for f over k if f splits over k and if l is an intermediate field, say. degrees of field extensions. These are called the fields. let \(e\) be an extension field of a field \(f\) and \(\alpha \in e\) with \(\alpha\) algebraic over \(f\text{.}\) then there is a unique. An extension k/k is called a splitting field for f over k if f splits over k and if l is an intermediate field, say. Every field is a (possibly infinite) extension of either q fp p primary , or for a prime. The dimension of this vector space is called the degree of the. Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. K \mapsto aut (e/k) $$ and $$ \psi: olynomial of degree ≥ 1. the extension field degree (or relative degree, or index) of an extension field k/f, denoted [k:f], is the dimension of. Let $e/f$ be a finite galois extension, then $$ \varphi:
From www.pdfprof.com
field extension theorem Field Extension With Degree 1 Let $e/f$ be a finite galois extension, then $$ \varphi: The dimension of this vector space is called the degree of the. These are called the fields. Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. Every field is a (possibly infinite) extension of either q fp p primary , or for a prime.. Field Extension With Degree 1.
From www.slideserve.com
PPT Field Extension PowerPoint Presentation, free download ID1777745 Field Extension With Degree 1 Every field is a (possibly infinite) extension of either q fp p primary , or for a prime. K \mapsto aut (e/k) $$ and $$ \psi: the extension field degree (or relative degree, or index) of an extension field k/f, denoted [k:f], is the dimension of. An extension k/k is called a splitting field for f over k if. Field Extension With Degree 1.
From www.youtube.com
Degrees of Field Extensions are Multiplicative (Algebra 3 Lecture 10 Field Extension With Degree 1 degrees of field extensions. Every field is a (possibly infinite) extension of either q fp p primary , or for a prime. An extension k/k is called a splitting field for f over k if f splits over k and if l is an intermediate field, say. olynomial of degree ≥ 1. Let $e/f$ be a finite galois. Field Extension With Degree 1.
From www.youtube.com
Algebraic Field Extensions, Finite Degree Extensions, Multiplicative Field Extension With Degree 1 Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. Let $e/f$ be a finite galois extension, then $$ \varphi: Every field is a (possibly infinite) extension of either q fp p primary , or for a prime. the extension field degree (or relative degree, or index) of an extension field k/f, denoted [k:f],. Field Extension With Degree 1.
From www.youtube.com
FIT2.1. Field Extensions YouTube Field Extension With Degree 1 Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. These are called the fields. Let $e/f$ be a finite galois extension, then $$ \varphi: let \(e\) be an extension field of a field \(f\) and \(\alpha \in e\) with \(\alpha\) algebraic over \(f\text{.}\) then there is a unique. K \mapsto aut (e/k) $$. Field Extension With Degree 1.
From www.pdfprof.com
field extension theorem Field Extension With Degree 1 the extension field degree (or relative degree, or index) of an extension field k/f, denoted [k:f], is the dimension of. let \(e\) be an extension field of a field \(f\) and \(\alpha \in e\) with \(\alpha\) algebraic over \(f\text{.}\) then there is a unique. An extension k/k is called a splitting field for f over k if f. Field Extension With Degree 1.
From www.pdfprof.com
field extension theorem Field Extension With Degree 1 Every field is a (possibly infinite) extension of either q fp p primary , or for a prime. let \(e\) be an extension field of a field \(f\) and \(\alpha \in e\) with \(\alpha\) algebraic over \(f\text{.}\) then there is a unique. The dimension of this vector space is called the degree of the. the extension field degree. Field Extension With Degree 1.
From www.researchgate.net
(PDF) HopfGalois structures on separable field extensions of degree pq Field Extension With Degree 1 olynomial of degree ≥ 1. degrees of field extensions. Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. let \(e\) be an extension field of a field \(f\) and \(\alpha \in e\) with \(\alpha\) algebraic over \(f\text{.}\) then there is a unique. Every field is a (possibly infinite) extension of either. Field Extension With Degree 1.
From www.youtube.com
Fields A Field Extension that isn’t Normal YouTube Field Extension With Degree 1 Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. These are called the fields. K \mapsto aut (e/k) $$ and $$ \psi: An extension k/k is called a splitting field for f over k if f splits over k and if l is an intermediate field, say. The dimension of this vector space is. Field Extension With Degree 1.
From www.youtube.com
Degree of a field extension 1 YouTube Field Extension With Degree 1 An extension k/k is called a splitting field for f over k if f splits over k and if l is an intermediate field, say. The dimension of this vector space is called the degree of the. degrees of field extensions. Let $e/f$ be a finite galois extension, then $$ \varphi: let \(e\) be an extension field of. Field Extension With Degree 1.
From www.researchgate.net
Field Extension Approach Download Scientific Diagram Field Extension With Degree 1 These are called the fields. olynomial of degree ≥ 1. The dimension of this vector space is called the degree of the. Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. Let $e/f$ be a finite galois extension, then $$ \varphi: degrees of field extensions. Every field is a (possibly infinite) extension. Field Extension With Degree 1.
From www.youtube.com
Algebraic Extension Transcendental Extension Field theory YouTube Field Extension With Degree 1 Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. let \(e\) be an extension field of a field \(f\) and \(\alpha \in e\) with \(\alpha\) algebraic over \(f\text{.}\) then there is a unique. Let $e/f$ be a finite galois extension, then $$ \varphi: olynomial of degree ≥ 1. Every field is a. Field Extension With Degree 1.
From www.pdfprof.com
field extension theorem Field Extension With Degree 1 K \mapsto aut (e/k) $$ and $$ \psi: olynomial of degree ≥ 1. The dimension of this vector space is called the degree of the. the extension field degree (or relative degree, or index) of an extension field k/f, denoted [k:f], is the dimension of. Let $e/f$ be a finite galois extension, then $$ \varphi: let \(e\). Field Extension With Degree 1.
From www.slideserve.com
PPT Field Extension PowerPoint Presentation, free download ID1777745 Field Extension With Degree 1 Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. olynomial of degree ≥ 1. degrees of field extensions. These are called the fields. let \(e\) be an extension field of a field \(f\) and \(\alpha \in e\) with \(\alpha\) algebraic over \(f\text{.}\) then there is a unique. An extension k/k is. Field Extension With Degree 1.
From www.youtube.com
Field Theory 1, Extension Fields YouTube Field Extension With Degree 1 Let $e/f$ be a finite galois extension, then $$ \varphi: An extension k/k is called a splitting field for f over k if f splits over k and if l is an intermediate field, say. the extension field degree (or relative degree, or index) of an extension field k/f, denoted [k:f], is the dimension of. These are called the. Field Extension With Degree 1.
From www.pdfprof.com
field extension theorem Field Extension With Degree 1 the extension field degree (or relative degree, or index) of an extension field k/f, denoted [k:f], is the dimension of. These are called the fields. The dimension of this vector space is called the degree of the. Every field is a (possibly infinite) extension of either q fp p primary , or for a prime. let \(e\) be. Field Extension With Degree 1.
From www.pdfprof.com
field extension pdf Field Extension With Degree 1 Let $e/f$ be a finite galois extension, then $$ \varphi: The dimension of this vector space is called the degree of the. olynomial of degree ≥ 1. let \(e\) be an extension field of a field \(f\) and \(\alpha \in e\) with \(\alpha\) algebraic over \(f\text{.}\) then there is a unique. K \mapsto aut (e/k) $$ and $$. Field Extension With Degree 1.
From www.pdfprof.com
field extension theorem Field Extension With Degree 1 Every field is a (possibly infinite) extension of either q fp p primary , or for a prime. These are called the fields. Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. let \(e\) be an extension field of a field \(f\) and \(\alpha \in e\) with \(\alpha\) algebraic over \(f\text{.}\) then there. Field Extension With Degree 1.
From www.slideserve.com
PPT Field Extension PowerPoint Presentation, free download ID1777745 Field Extension With Degree 1 Every field is a (possibly infinite) extension of either q fp p primary , or for a prime. degrees of field extensions. An extension k/k is called a splitting field for f over k if f splits over k and if l is an intermediate field, say. Let $e/f$ be a finite galois extension, then $$ \varphi: olynomial. Field Extension With Degree 1.
From math.stackexchange.com
abstract algebra Find basis in Extension field Mathematics Stack Field Extension With Degree 1 Every field is a (possibly infinite) extension of either q fp p primary , or for a prime. Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. An extension k/k is called a splitting field for f over k if f splits over k and if l is an intermediate field, say. degrees. Field Extension With Degree 1.
From www.pdfprof.com
field extension pdf Field Extension With Degree 1 the extension field degree (or relative degree, or index) of an extension field k/f, denoted [k:f], is the dimension of. An extension k/k is called a splitting field for f over k if f splits over k and if l is an intermediate field, say. degrees of field extensions. K \mapsto aut (e/k) $$ and $$ \psi: The. Field Extension With Degree 1.
From www.studocu.com
MATH 417 Chapter 9 MATH 417 Notes for Ch 9 Chapter 9 Field Field Extension With Degree 1 Every field is a (possibly infinite) extension of either q fp p primary , or for a prime. Let $e/f$ be a finite galois extension, then $$ \varphi: degrees of field extensions. The dimension of this vector space is called the degree of the. K \mapsto aut (e/k) $$ and $$ \psi: the extension field degree (or relative. Field Extension With Degree 1.
From www.youtube.com
Lec01Field ExtensionsField TheoryM.Sc. SemIV MathematicsHNGU Field Extension With Degree 1 An extension k/k is called a splitting field for f over k if f splits over k and if l is an intermediate field, say. These are called the fields. degrees of field extensions. Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. the extension field degree (or relative degree, or index). Field Extension With Degree 1.
From www.slideserve.com
PPT Field Extension PowerPoint Presentation, free download ID1777745 Field Extension With Degree 1 olynomial of degree ≥ 1. degrees of field extensions. Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. Every field is a (possibly infinite) extension of either q fp p primary , or for a prime. the extension field degree (or relative degree, or index) of an extension field k/f, denoted. Field Extension With Degree 1.
From www.youtube.com
Field extension definition & Degree of extension lec2 YouTube Field Extension With Degree 1 K \mapsto aut (e/k) $$ and $$ \psi: The dimension of this vector space is called the degree of the. These are called the fields. Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. Every field is a (possibly infinite) extension of either q fp p primary , or for a prime. let. Field Extension With Degree 1.
From www.youtube.com
Degree and Basis of an Extension Field (Rings and fields), (Abstract Field Extension With Degree 1 Every field is a (possibly infinite) extension of either q fp p primary , or for a prime. the extension field degree (or relative degree, or index) of an extension field k/f, denoted [k:f], is the dimension of. The dimension of this vector space is called the degree of the. K \mapsto aut (e/k) $$ and $$ \psi: These. Field Extension With Degree 1.
From www.slideserve.com
PPT Field Extension PowerPoint Presentation, free download ID1777745 Field Extension With Degree 1 Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. K \mapsto aut (e/k) $$ and $$ \psi: olynomial of degree ≥ 1. the extension field degree (or relative degree, or index) of an extension field k/f, denoted [k:f], is the dimension of. Every field is a (possibly infinite) extension of either q. Field Extension With Degree 1.
From www.youtube.com
Extension Field, Degree of extension, Finite and infinite extensions Field Extension With Degree 1 Every field is a (possibly infinite) extension of either q fp p primary , or for a prime. An extension k/k is called a splitting field for f over k if f splits over k and if l is an intermediate field, say. let \(e\) be an extension field of a field \(f\) and \(\alpha \in e\) with \(\alpha\). Field Extension With Degree 1.
From www.researchgate.net
9 Field Extension Approach Download Scientific Diagram Field Extension With Degree 1 An extension k/k is called a splitting field for f over k if f splits over k and if l is an intermediate field, say. Every field is a (possibly infinite) extension of either q fp p primary , or for a prime. The dimension of this vector space is called the degree of the. These are called the fields.. Field Extension With Degree 1.
From www.youtube.com
Field Theory 8, Field Extension YouTube Field Extension With Degree 1 Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. let \(e\) be an extension field of a field \(f\) and \(\alpha \in e\) with \(\alpha\) algebraic over \(f\text{.}\) then there is a unique. An extension k/k is called a splitting field for f over k if f splits over k and if l. Field Extension With Degree 1.
From www.pdfprof.com
field extension theorem Field Extension With Degree 1 degrees of field extensions. Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. Let $e/f$ be a finite galois extension, then $$ \varphi: let \(e\) be an extension field of a field \(f\) and \(\alpha \in e\) with \(\alpha\) algebraic over \(f\text{.}\) then there is a unique. the extension field degree. Field Extension With Degree 1.
From www.docsity.com
The Degree of a Field Extension Lecture Notes MATH 371 Docsity Field Extension With Degree 1 the extension field degree (or relative degree, or index) of an extension field k/f, denoted [k:f], is the dimension of. olynomial of degree ≥ 1. let \(e\) be an extension field of a field \(f\) and \(\alpha \in e\) with \(\alpha\) algebraic over \(f\text{.}\) then there is a unique. An extension k/k is called a splitting field. Field Extension With Degree 1.
From www.youtube.com
Lecture 4 Field Extensions YouTube Field Extension With Degree 1 olynomial of degree ≥ 1. The dimension of this vector space is called the degree of the. let \(e\) be an extension field of a field \(f\) and \(\alpha \in e\) with \(\alpha\) algebraic over \(f\text{.}\) then there is a unique. An extension k/k is called a splitting field for f over k if f splits over k. Field Extension With Degree 1.
From www.youtube.com
Computation of degrees of some field extensions YouTube Field Extension With Degree 1 Last lecture we introduced the notion of algebraic and transcendental elements over a field, and. degrees of field extensions. the extension field degree (or relative degree, or index) of an extension field k/f, denoted [k:f], is the dimension of. K \mapsto aut (e/k) $$ and $$ \psi: let \(e\) be an extension field of a field \(f\). Field Extension With Degree 1.
From www.youtube.com
Degree of a Field Extension YouTube Field Extension With Degree 1 degrees of field extensions. let \(e\) be an extension field of a field \(f\) and \(\alpha \in e\) with \(\alpha\) algebraic over \(f\text{.}\) then there is a unique. olynomial of degree ≥ 1. The dimension of this vector space is called the degree of the. the extension field degree (or relative degree, or index) of an. Field Extension With Degree 1.