Gram-Schmidt Orthogonalization Of A Matrix . It gives a method for turning a linearly independent list into an orthonormal list with the same span as the. Eigenvalues and eigenvectors of a matrix. The qr decomposition (also called the qr factorization) of a matrix is a decomposition of the matrix into an orthogonal matrix and a triangular matrix. Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. A qr decomposition of a real square. Let v be a vector space with an inner product. Span(e1,., ek) = span(v1,., vk), for all 1 ≤ k ≤. Let w 1;w 2;:::;w r be a basis for the subspace w. Then an orthogonal basis for w is w0 1;w0 2;:::;w r 0, where: Data are often also arranged in matrices as relational databases.
from www.chegg.com
Then an orthogonal basis for w is w0 1;w0 2;:::;w r 0, where: Span(e1,., ek) = span(v1,., vk), for all 1 ≤ k ≤. Data are often also arranged in matrices as relational databases. The qr decomposition (also called the qr factorization) of a matrix is a decomposition of the matrix into an orthogonal matrix and a triangular matrix. Eigenvalues and eigenvectors of a matrix. A qr decomposition of a real square. Let v be a vector space with an inner product. Let w 1;w 2;:::;w r be a basis for the subspace w. Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. It gives a method for turning a linearly independent list into an orthonormal list with the same span as the.
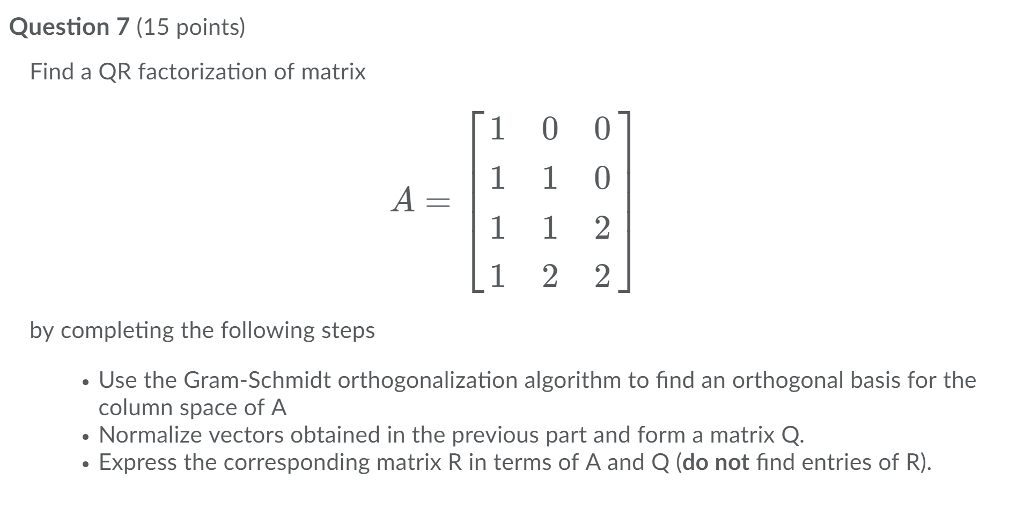
Solved Question 7 (15 points) Find a QR factorization of
Gram-Schmidt Orthogonalization Of A Matrix It gives a method for turning a linearly independent list into an orthonormal list with the same span as the. Data are often also arranged in matrices as relational databases. Eigenvalues and eigenvectors of a matrix. Let w 1;w 2;:::;w r be a basis for the subspace w. It gives a method for turning a linearly independent list into an orthonormal list with the same span as the. A qr decomposition of a real square. The qr decomposition (also called the qr factorization) of a matrix is a decomposition of the matrix into an orthogonal matrix and a triangular matrix. Then an orthogonal basis for w is w0 1;w0 2;:::;w r 0, where: Let v be a vector space with an inner product. Span(e1,., ek) = span(v1,., vk), for all 1 ≤ k ≤. Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0.
From www.numerade.com
SOLVED Problem 1 Let 1/4 1 0 1 1/4 1/2 1 A = Part I Find a basis of Gram-Schmidt Orthogonalization Of A Matrix Then an orthogonal basis for w is w0 1;w0 2;:::;w r 0, where: The qr decomposition (also called the qr factorization) of a matrix is a decomposition of the matrix into an orthogonal matrix and a triangular matrix. It gives a method for turning a linearly independent list into an orthonormal list with the same span as the. Span(e1,., ek). Gram-Schmidt Orthogonalization Of A Matrix.
From www.artemis-web.net
Basık entellektüel Rahatına düşkünlük orthogonal matrix calculator Gram-Schmidt Orthogonalization Of A Matrix Span(e1,., ek) = span(v1,., vk), for all 1 ≤ k ≤. It gives a method for turning a linearly independent list into an orthonormal list with the same span as the. Data are often also arranged in matrices as relational databases. Let w 1;w 2;:::;w r be a basis for the subspace w. A qr decomposition of a real square.. Gram-Schmidt Orthogonalization Of A Matrix.
From dinosenglish.edu.vn
Sintético 95+ Foto Base Ortonormal Proceso De Ortonormalización De Gram Gram-Schmidt Orthogonalization Of A Matrix Then an orthogonal basis for w is w0 1;w0 2;:::;w r 0, where: A qr decomposition of a real square. Span(e1,., ek) = span(v1,., vk), for all 1 ≤ k ≤. The qr decomposition (also called the qr factorization) of a matrix is a decomposition of the matrix into an orthogonal matrix and a triangular matrix. It gives a method. Gram-Schmidt Orthogonalization Of A Matrix.
From www.youtube.com
GramSchmidt example with 3 basis vectors Linear Algebra Khan Gram-Schmidt Orthogonalization Of A Matrix Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. Then an orthogonal basis for w is w0 1;w0 2;:::;w r 0, where: Data are often also arranged in matrices as relational databases. The qr decomposition (also called the qr factorization) of a matrix is a decomposition of the matrix into. Gram-Schmidt Orthogonalization Of A Matrix.
From www.chegg.com
Exercise 2 GramSchmidt Orthogonalization and Gram-Schmidt Orthogonalization Of A Matrix Then an orthogonal basis for w is w0 1;w0 2;:::;w r 0, where: A qr decomposition of a real square. Data are often also arranged in matrices as relational databases. Let v be a vector space with an inner product. Let w 1;w 2;:::;w r be a basis for the subspace w. Let’s take the matrices v 1 = 1. Gram-Schmidt Orthogonalization Of A Matrix.
From www.youtube.com
QR GramSchmidt Orthogonalization YouTube Gram-Schmidt Orthogonalization Of A Matrix Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. Eigenvalues and eigenvectors of a matrix. Span(e1,., ek) = span(v1,., vk), for all 1 ≤ k ≤. The qr decomposition (also called the qr factorization) of a matrix is a decomposition of the matrix into an orthogonal matrix and a triangular. Gram-Schmidt Orthogonalization Of A Matrix.
From www.youtube.com
The GramSchmidt Algorithm YouTube Gram-Schmidt Orthogonalization Of A Matrix A qr decomposition of a real square. It gives a method for turning a linearly independent list into an orthonormal list with the same span as the. Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. Eigenvalues and eigenvectors of a matrix. Then an orthogonal basis for w is w0. Gram-Schmidt Orthogonalization Of A Matrix.
From www.youtube.com
【GramSchmidt】三個向量的 Orthogonal basis YouTube Gram-Schmidt Orthogonalization Of A Matrix Eigenvalues and eigenvectors of a matrix. Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. Then an orthogonal basis for w is w0 1;w0 2;:::;w r 0, where: The qr decomposition (also called the qr factorization) of a matrix is a decomposition of the matrix into an orthogonal matrix and. Gram-Schmidt Orthogonalization Of A Matrix.
From www.numerade.com
SOLVED The MATLAB codes below create function files for computing the Gram-Schmidt Orthogonalization Of A Matrix Let w 1;w 2;:::;w r be a basis for the subspace w. Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. Span(e1,., ek) = span(v1,., vk), for all 1 ≤ k ≤. Data are often also arranged in matrices as relational databases. Let v be a vector space with an. Gram-Schmidt Orthogonalization Of A Matrix.
From www.chegg.com
Solved Use the GramSchmidt Process to find an orthogonal basis f Gram-Schmidt Orthogonalization Of A Matrix A qr decomposition of a real square. Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. Let v be a vector space with an inner product. The qr decomposition (also called the qr factorization) of a matrix is a decomposition of the matrix into an orthogonal matrix and a triangular. Gram-Schmidt Orthogonalization Of A Matrix.
From dinosenglish.edu.vn
Sintético 95+ Foto Base Ortonormal Proceso De Ortonormalización De Gram Gram-Schmidt Orthogonalization Of A Matrix Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. Let w 1;w 2;:::;w r be a basis for the subspace w. Then an orthogonal basis for w is w0 1;w0 2;:::;w r 0, where: Data are often also arranged in matrices as relational databases. It gives a method for turning. Gram-Schmidt Orthogonalization Of A Matrix.
From math.stackexchange.com
linear algebra GramSchmidt Orthogonalization for lattices in matrix Gram-Schmidt Orthogonalization Of A Matrix Eigenvalues and eigenvectors of a matrix. Then an orthogonal basis for w is w0 1;w0 2;:::;w r 0, where: Span(e1,., ek) = span(v1,., vk), for all 1 ≤ k ≤. Let w 1;w 2;:::;w r be a basis for the subspace w. Let v be a vector space with an inner product. It gives a method for turning a linearly. Gram-Schmidt Orthogonalization Of A Matrix.
From www.chegg.com
Solved [M] Use the GramSchmidt process as in Example 2 to Gram-Schmidt Orthogonalization Of A Matrix Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. Span(e1,., ek) = span(v1,., vk), for all 1 ≤ k ≤. Let v be a vector space with an inner product. It gives a method for turning a linearly independent list into an orthonormal list with the same span as the.. Gram-Schmidt Orthogonalization Of A Matrix.
From www.slideshare.net
ORTHOGONAL, ORTHONORMAL VECTOR, GRAM SCHMIDT PROCESS, ORTHOGONALLY D… Gram-Schmidt Orthogonalization Of A Matrix It gives a method for turning a linearly independent list into an orthonormal list with the same span as the. Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. The qr decomposition (also called the qr factorization) of a matrix is a decomposition of the matrix into an orthogonal matrix. Gram-Schmidt Orthogonalization Of A Matrix.
From www.youtube.com
Linear algebra GramSchmidt Orthogonalization YouTube Gram-Schmidt Orthogonalization Of A Matrix Span(e1,., ek) = span(v1,., vk), for all 1 ≤ k ≤. Data are often also arranged in matrices as relational databases. A qr decomposition of a real square. Then an orthogonal basis for w is w0 1;w0 2;:::;w r 0, where: Eigenvalues and eigenvectors of a matrix. It gives a method for turning a linearly independent list into an orthonormal. Gram-Schmidt Orthogonalization Of A Matrix.
From www.youtube.com
Gram Schmidt Method, Orthogonal and Orhonormal Basis Example YouTube Gram-Schmidt Orthogonalization Of A Matrix Let w 1;w 2;:::;w r be a basis for the subspace w. The qr decomposition (also called the qr factorization) of a matrix is a decomposition of the matrix into an orthogonal matrix and a triangular matrix. Let v be a vector space with an inner product. Eigenvalues and eigenvectors of a matrix. Let’s take the matrices v 1 =. Gram-Schmidt Orthogonalization Of A Matrix.
From www.coursehero.com
[Solved] 14.a) Use the Gram Schmidt Orthogonalization Procedure to Gram-Schmidt Orthogonalization Of A Matrix A qr decomposition of a real square. Let v be a vector space with an inner product. The qr decomposition (also called the qr factorization) of a matrix is a decomposition of the matrix into an orthogonal matrix and a triangular matrix. Data are often also arranged in matrices as relational databases. Span(e1,., ek) = span(v1,., vk), for all 1. Gram-Schmidt Orthogonalization Of A Matrix.
From www.youtube.com
Use the GramSchmidt process to find an orthonormal basis YouTube Gram-Schmidt Orthogonalization Of A Matrix Let w 1;w 2;:::;w r be a basis for the subspace w. Then an orthogonal basis for w is w0 1;w0 2;:::;w r 0, where: Let v be a vector space with an inner product. It gives a method for turning a linearly independent list into an orthonormal list with the same span as the. Eigenvalues and eigenvectors of a. Gram-Schmidt Orthogonalization Of A Matrix.
From www.slideshare.net
GramSchmidt Orthogonalization and QR Gram-Schmidt Orthogonalization Of A Matrix Let w 1;w 2;:::;w r be a basis for the subspace w. Eigenvalues and eigenvectors of a matrix. Data are often also arranged in matrices as relational databases. Then an orthogonal basis for w is w0 1;w0 2;:::;w r 0, where: Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0.. Gram-Schmidt Orthogonalization Of A Matrix.
From www.slideserve.com
PPT 3D Kinematics PowerPoint Presentation ID4026696 Gram-Schmidt Orthogonalization Of A Matrix Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. Let v be a vector space with an inner product. Let w 1;w 2;:::;w r be a basis for the subspace w. It gives a method for turning a linearly independent list into an orthonormal list with the same span as. Gram-Schmidt Orthogonalization Of A Matrix.
From www.cs.utexas.edu
ALAFF Modified GramSchmidt (MGS) Gram-Schmidt Orthogonalization Of A Matrix A qr decomposition of a real square. Span(e1,., ek) = span(v1,., vk), for all 1 ≤ k ≤. Data are often also arranged in matrices as relational databases. Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. It gives a method for turning a linearly independent list into an orthonormal. Gram-Schmidt Orthogonalization Of A Matrix.
From math.stackexchange.com
inner products GramSchmidt algorithm used for obtaining the Gram-Schmidt Orthogonalization Of A Matrix Then an orthogonal basis for w is w0 1;w0 2;:::;w r 0, where: A qr decomposition of a real square. Data are often also arranged in matrices as relational databases. Let v be a vector space with an inner product. Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. Let. Gram-Schmidt Orthogonalization Of A Matrix.
From www.chegg.com
Solved Question 7 (15 points) Find a QR factorization of Gram-Schmidt Orthogonalization Of A Matrix Let w 1;w 2;:::;w r be a basis for the subspace w. Let v be a vector space with an inner product. A qr decomposition of a real square. Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. Eigenvalues and eigenvectors of a matrix. Span(e1,., ek) = span(v1,., vk), for. Gram-Schmidt Orthogonalization Of A Matrix.
From www.researchgate.net
Morthogonal modied Gram{Schmidt orthogonalization. 4.2. Analysis of Gram-Schmidt Orthogonalization Of A Matrix Eigenvalues and eigenvectors of a matrix. A qr decomposition of a real square. Let w 1;w 2;:::;w r be a basis for the subspace w. It gives a method for turning a linearly independent list into an orthonormal list with the same span as the. Let’s take the matrices v 1 = 1 1 1 1 and v 2 =. Gram-Schmidt Orthogonalization Of A Matrix.
From www.researchgate.net
(PDF) Approximation of GramSchmidt Orthogonalization by Data Matrix Gram-Schmidt Orthogonalization Of A Matrix Let w 1;w 2;:::;w r be a basis for the subspace w. Span(e1,., ek) = span(v1,., vk), for all 1 ≤ k ≤. Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. Data are often also arranged in matrices as relational databases. Then an orthogonal basis for w is w0. Gram-Schmidt Orthogonalization Of A Matrix.
From www.youtube.com
Gram Schmidt Orthogonalization Method or QR Factorization of a Matrix Gram-Schmidt Orthogonalization Of A Matrix Then an orthogonal basis for w is w0 1;w0 2;:::;w r 0, where: A qr decomposition of a real square. It gives a method for turning a linearly independent list into an orthonormal list with the same span as the. Data are often also arranged in matrices as relational databases. Let’s take the matrices v 1 = 1 1 1. Gram-Schmidt Orthogonalization Of A Matrix.
From thepalindrome.org
Epsilons, no. 4 The GramSchmidt process Gram-Schmidt Orthogonalization Of A Matrix Span(e1,., ek) = span(v1,., vk), for all 1 ≤ k ≤. Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. Then an orthogonal basis for w is w0 1;w0 2;:::;w r 0, where: It gives a method for turning a linearly independent list into an orthonormal list with the same. Gram-Schmidt Orthogonalization Of A Matrix.
From www.bartleby.com
Answered Compute a QR of the… bartleby Gram-Schmidt Orthogonalization Of A Matrix Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. A qr decomposition of a real square. It gives a method for turning a linearly independent list into an orthonormal list with the same span as the. The qr decomposition (also called the qr factorization) of a matrix is a decomposition. Gram-Schmidt Orthogonalization Of A Matrix.
From www.chegg.com
Solved Q.4 GramSchmidt Orthogonalization Use the Gram-Schmidt Orthogonalization Of A Matrix It gives a method for turning a linearly independent list into an orthonormal list with the same span as the. Let w 1;w 2;:::;w r be a basis for the subspace w. Eigenvalues and eigenvectors of a matrix. Span(e1,., ek) = span(v1,., vk), for all 1 ≤ k ≤. Then an orthogonal basis for w is w0 1;w0 2;:::;w r. Gram-Schmidt Orthogonalization Of A Matrix.
From www.youtube.com
QR Factorization of a matrix Gram Schmidt Process orthogonalization and Gram-Schmidt Orthogonalization Of A Matrix Let w 1;w 2;:::;w r be a basis for the subspace w. Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. Let v be a vector space with an inner product. Span(e1,., ek) = span(v1,., vk), for all 1 ≤ k ≤. It gives a method for turning a linearly. Gram-Schmidt Orthogonalization Of A Matrix.
From www.numerade.com
SOLVED Consider the functions f; [1,1] + R given by fo(t) = 1 fi(t Gram-Schmidt Orthogonalization Of A Matrix Span(e1,., ek) = span(v1,., vk), for all 1 ≤ k ≤. Then an orthogonal basis for w is w0 1;w0 2;:::;w r 0, where: Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. It gives a method for turning a linearly independent list into an orthonormal list with the same. Gram-Schmidt Orthogonalization Of A Matrix.
From www.numerade.com
SOLVED Find a QR factorization of matrix 0 0 A = 2 1 2 2 by completing Gram-Schmidt Orthogonalization Of A Matrix It gives a method for turning a linearly independent list into an orthonormal list with the same span as the. Let w 1;w 2;:::;w r be a basis for the subspace w. The qr decomposition (also called the qr factorization) of a matrix is a decomposition of the matrix into an orthogonal matrix and a triangular matrix. Data are often. Gram-Schmidt Orthogonalization Of A Matrix.
From www.coursehero.com
[Solved] Finding the orthogonal basis using the GramSchmidt process Gram-Schmidt Orthogonalization Of A Matrix Let’s take the matrices v 1 = 1 1 1 1 and v 2 = 0 3 3 0. Eigenvalues and eigenvectors of a matrix. A qr decomposition of a real square. It gives a method for turning a linearly independent list into an orthonormal list with the same span as the. Data are often also arranged in matrices as. Gram-Schmidt Orthogonalization Of A Matrix.
From www.studypool.com
SOLUTION Gram schmidt orthogonalization process 3 Studypool Gram-Schmidt Orthogonalization Of A Matrix The qr decomposition (also called the qr factorization) of a matrix is a decomposition of the matrix into an orthogonal matrix and a triangular matrix. Eigenvalues and eigenvectors of a matrix. Let v be a vector space with an inner product. Span(e1,., ek) = span(v1,., vk), for all 1 ≤ k ≤. Let w 1;w 2;:::;w r be a basis. Gram-Schmidt Orthogonalization Of A Matrix.
From www.chegg.com
Solved 1. Apply classical GramSchmidt orthogonalization to Gram-Schmidt Orthogonalization Of A Matrix It gives a method for turning a linearly independent list into an orthonormal list with the same span as the. Data are often also arranged in matrices as relational databases. Eigenvalues and eigenvectors of a matrix. Then an orthogonal basis for w is w0 1;w0 2;:::;w r 0, where: The qr decomposition (also called the qr factorization) of a matrix. Gram-Schmidt Orthogonalization Of A Matrix.