What Is The Standard Inner Product . an inner product on a vector space v over f is a function h;i: we discuss inner products on nite dimensional real and complex vector spaces. the dot product is the standard inner product on $\mathbb r^n$. In a vector space, it is a way to multiply vectors. We define the standard inner product on r^n and explain its. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. In general, any symmetric, positive definite. an inner product is a generalization of the dot product. given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\) be. Although we are mainly interested in.
from www.chegg.com
We define the standard inner product on r^n and explain its. In general, any symmetric, positive definite. Although we are mainly interested in. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. the dot product is the standard inner product on $\mathbb r^n$. an inner product is a generalization of the dot product. given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\) be. In a vector space, it is a way to multiply vectors. an inner product on a vector space v over f is a function h;i: we discuss inner products on nite dimensional real and complex vector spaces.
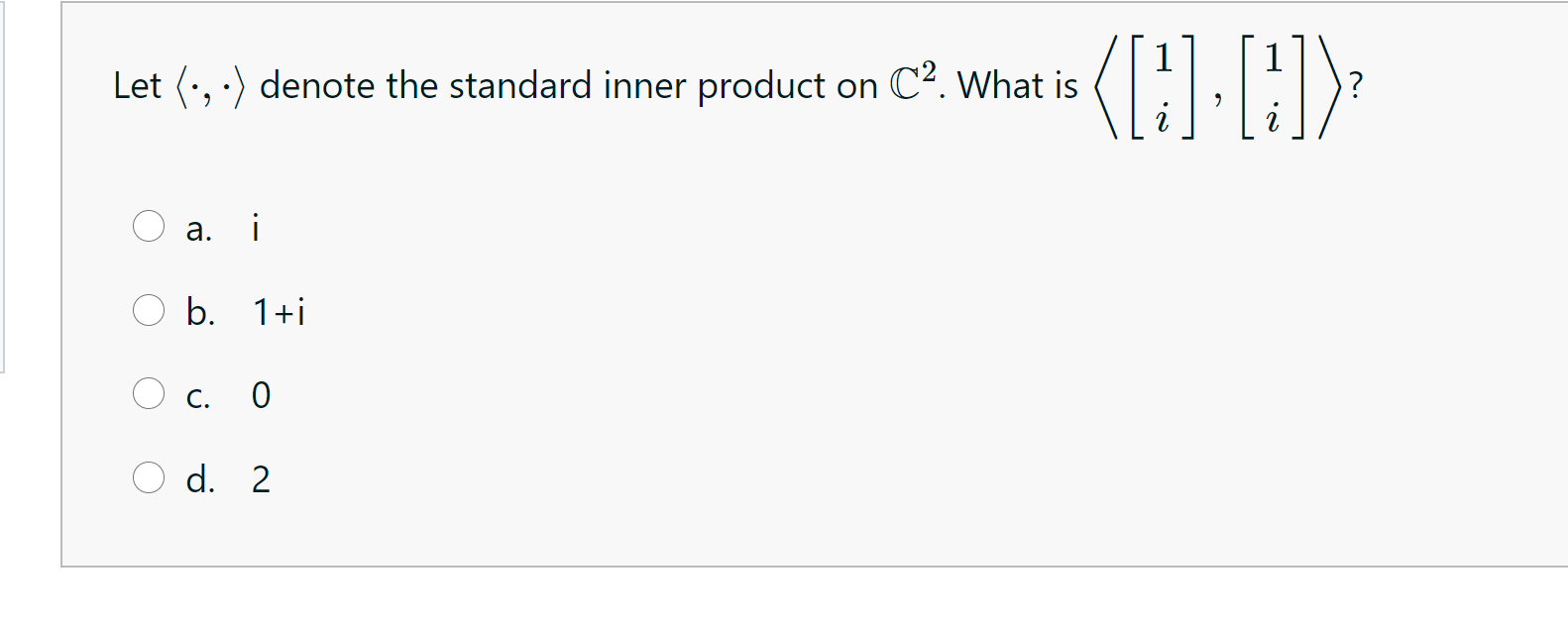
Solved Let ( •) denote the standard inner product on C2.
What Is The Standard Inner Product We define the standard inner product on r^n and explain its. we discuss inner products on nite dimensional real and complex vector spaces. the dot product is the standard inner product on $\mathbb r^n$. given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\) be. Although we are mainly interested in. an inner product is a generalization of the dot product. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. In a vector space, it is a way to multiply vectors. In general, any symmetric, positive definite. an inner product on a vector space v over f is a function h;i: We define the standard inner product on r^n and explain its.
From www.youtube.com
Linear Algebra Inner Product YouTube What Is The Standard Inner Product Although we are mainly interested in. In general, any symmetric, positive definite. We define the standard inner product on r^n and explain its. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\) be. an inner product is a generalization. What Is The Standard Inner Product.
From www.slideserve.com
PPT Inner Product PowerPoint Presentation, free download ID2663418 What Is The Standard Inner Product the dot product is the standard inner product on $\mathbb r^n$. an inner product is a generalization of the dot product. given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\) be. In general, any symmetric, positive definite. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. We. What Is The Standard Inner Product.
From www.slideserve.com
PPT Elementary Linear Algebra Anton & Rorres, 9 th Edition PowerPoint What Is The Standard Inner Product given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\) be. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. We define the standard inner product on r^n and explain its. we discuss inner products on nite dimensional real and complex vector spaces. the dot product is the. What Is The Standard Inner Product.
From www.chegg.com
Solved Consider R3 with the standard inner product given by What Is The Standard Inner Product we discuss inner products on nite dimensional real and complex vector spaces. given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\) be. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. an inner product on a vector space v over f is a function h;i: Although we. What Is The Standard Inner Product.
From www.chegg.com
Solved (a) Consider the standard inner product (u, v) = u.v What Is The Standard Inner Product an inner product on a vector space v over f is a function h;i: In general, any symmetric, positive definite. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\) be. In a vector space, it is a way to. What Is The Standard Inner Product.
From www.youtube.com
Inner Product Spaces YouTube What Is The Standard Inner Product In general, any symmetric, positive definite. an inner product is a generalization of the dot product. given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\) be. an inner product on a vector space v over f is a function h;i: Although we are mainly interested in. we discuss inner products on nite dimensional. What Is The Standard Inner Product.
From www.slideserve.com
PPT Elementary Linear Algebra Anton & Rorres, 9 th Edition PowerPoint What Is The Standard Inner Product an inner product is a generalization of the dot product. we discuss inner products on nite dimensional real and complex vector spaces. an inner product on a vector space v over f is a function h;i: In general, any symmetric, positive definite. In a vector space, it is a way to multiply vectors. Although we are mainly. What Is The Standard Inner Product.
From www.chegg.com
Solved Calculate the standard inner product of the two What Is The Standard Inner Product We define the standard inner product on r^n and explain its. the dot product is the standard inner product on $\mathbb r^n$. Although we are mainly interested in. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. In a vector space, it is a way to multiply vectors. an inner product. What Is The Standard Inner Product.
From studylib.net
Inner Product Space What Is The Standard Inner Product In a vector space, it is a way to multiply vectors. We define the standard inner product on r^n and explain its. an inner product on a vector space v over f is a function h;i: we discuss inner products on nite dimensional real and complex vector spaces. given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1,. What Is The Standard Inner Product.
From www.youtube.com
Lecture 25 Inner Product Spaces YouTube What Is The Standard Inner Product given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\) be. the dot product is the standard inner product on $\mathbb r^n$. In a vector space, it is a way to multiply vectors. an inner product on a vector space v over f is a function h;i: Although we are mainly interested in. In general,. What Is The Standard Inner Product.
From www.slideserve.com
PPT 4.10 Inner Product Spaces PowerPoint Presentation ID6416031 What Is The Standard Inner Product the dot product is the standard inner product on $\mathbb r^n$. given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\) be. Although we are mainly interested in. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. an inner product is a generalization of the dot product. . What Is The Standard Inner Product.
From www.chegg.com
Solved In Exercises 910, compute the standard inner product What Is The Standard Inner Product Although we are mainly interested in. an inner product is a generalization of the dot product. the dot product is the standard inner product on $\mathbb r^n$. given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\) be. We define the standard inner product on r^n and explain its. V v !f satisfying (i) hv;vi. What Is The Standard Inner Product.
From www.slideserve.com
PPT 4.10 Inner Product Spaces PowerPoint Presentation ID6416031 What Is The Standard Inner Product We define the standard inner product on r^n and explain its. we discuss inner products on nite dimensional real and complex vector spaces. the dot product is the standard inner product on $\mathbb r^n$. an inner product on a vector space v over f is a function h;i: In a vector space, it is a way to. What Is The Standard Inner Product.
From math.stackexchange.com
linear algebra How can an inner product be defined through a proof What Is The Standard Inner Product we discuss inner products on nite dimensional real and complex vector spaces. an inner product on a vector space v over f is a function h;i: We define the standard inner product on r^n and explain its. Although we are mainly interested in. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0. What Is The Standard Inner Product.
From www.numerade.com
⏩SOLVEDVerify that the standard inner product on ℂ^n is a complex What Is The Standard Inner Product given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\) be. an inner product on a vector space v over f is a function h;i: Although we are mainly interested in. we discuss inner products on nite dimensional real and complex vector spaces. an inner product is a generalization of the dot product. V. What Is The Standard Inner Product.
From www.chegg.com
Solved (5 points) Using the standard inner product, find all What Is The Standard Inner Product V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. an inner product on a vector space v over f is a function h;i: an inner product is a generalization of the dot product. we discuss inner products on nite dimensional real and complex vector spaces. In a vector space, it. What Is The Standard Inner Product.
From www.slideserve.com
PPT CHAPTER 5 INNER PRODUCT SPACES PowerPoint Presentation, free What Is The Standard Inner Product V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. an inner product is a generalization of the dot product. We define the standard inner product on r^n and explain its. we discuss inner products on nite dimensional real and complex vector spaces. In a vector space, it is a way to. What Is The Standard Inner Product.
From www.youtube.com
Representation Theory 6, Standard Inner Product, Orthogonal and What Is The Standard Inner Product an inner product on a vector space v over f is a function h;i: We define the standard inner product on r^n and explain its. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. we discuss inner products on nite dimensional real and complex vector spaces. an inner product is. What Is The Standard Inner Product.
From documentmodele.blogspot.com
Document modèle Inner product norm What Is The Standard Inner Product the dot product is the standard inner product on $\mathbb r^n$. an inner product on a vector space v over f is a function h;i: In general, any symmetric, positive definite. we discuss inner products on nite dimensional real and complex vector spaces. Although we are mainly interested in. an inner product is a generalization of. What Is The Standard Inner Product.
From www.deep-mind.org
Inner Products, Norms and Metrics deep mind What Is The Standard Inner Product we discuss inner products on nite dimensional real and complex vector spaces. We define the standard inner product on r^n and explain its. given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\) be. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. an inner product is a. What Is The Standard Inner Product.
From www.chegg.com
Solved Let ( ) be thw standard inner product on R^2, and What Is The Standard Inner Product Although we are mainly interested in. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. In general, any symmetric, positive definite. an inner product on a vector space v over f is a function h;i: an inner product is a generalization of the dot product. In a vector space, it is. What Is The Standard Inner Product.
From www.youtube.com
The Standard Inner Product on R^n YouTube What Is The Standard Inner Product We define the standard inner product on r^n and explain its. the dot product is the standard inner product on $\mathbb r^n$. Although we are mainly interested in. In general, any symmetric, positive definite. an inner product on a vector space v over f is a function h;i: given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1,. What Is The Standard Inner Product.
From www.youtube.com
Frobenius Inner product, proof by definition YouTube What Is The Standard Inner Product We define the standard inner product on r^n and explain its. Although we are mainly interested in. the dot product is the standard inner product on $\mathbb r^n$. an inner product on a vector space v over f is a function h;i: given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\) be. In general,. What Is The Standard Inner Product.
From www.slideserve.com
PPT 4.10 Inner Product Spaces PowerPoint Presentation ID6416031 What Is The Standard Inner Product the dot product is the standard inner product on $\mathbb r^n$. We define the standard inner product on r^n and explain its. we discuss inner products on nite dimensional real and complex vector spaces. In general, any symmetric, positive definite. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. an. What Is The Standard Inner Product.
From www.youtube.com
Inner product vs dot product YouTube What Is The Standard Inner Product we discuss inner products on nite dimensional real and complex vector spaces. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. the dot product is the standard inner product on $\mathbb r^n$. Although we are mainly interested in. given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\). What Is The Standard Inner Product.
From www.slideserve.com
PPT Chapter 5 Inner Product Spaces PowerPoint Presentation, free What Is The Standard Inner Product In a vector space, it is a way to multiply vectors. an inner product is a generalization of the dot product. In general, any symmetric, positive definite. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. the dot product is the standard inner product on $\mathbb r^n$. an inner product. What Is The Standard Inner Product.
From www.chegg.com
Solved Let ( •) denote the standard inner product on C2. What Is The Standard Inner Product we discuss inner products on nite dimensional real and complex vector spaces. We define the standard inner product on r^n and explain its. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. Although we are mainly interested in. In a vector space, it is a way to multiply vectors. In general, any. What Is The Standard Inner Product.
From www.youtube.com
Linear Algebra 33 Transpose and Inner Product YouTube What Is The Standard Inner Product In general, any symmetric, positive definite. the dot product is the standard inner product on $\mathbb r^n$. we discuss inner products on nite dimensional real and complex vector spaces. We define the standard inner product on r^n and explain its. given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\) be. an inner product. What Is The Standard Inner Product.
From www.youtube.com
Inner Product and Orthogonal Functions , Quick Example YouTube What Is The Standard Inner Product we discuss inner products on nite dimensional real and complex vector spaces. In a vector space, it is a way to multiply vectors. We define the standard inner product on r^n and explain its. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let. What Is The Standard Inner Product.
From www.chegg.com
Solved (26. (20 pts)) Using the standard inner product, What Is The Standard Inner Product the dot product is the standard inner product on $\mathbb r^n$. V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. Although we are mainly interested in. In a vector space, it is a way to multiply vectors. we discuss inner products on nite dimensional real and complex vector spaces. given. What Is The Standard Inner Product.
From www.chegg.com
Solved (a) Prove that the standard inner product on R2 What Is The Standard Inner Product In general, any symmetric, positive definite. We define the standard inner product on r^n and explain its. Although we are mainly interested in. given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\), let \(\left\{\mathbf{e}_1, \mathbf{e}_2, \ldots, \mathbf{e}_n\right\}\) be. the dot product is the standard inner product on $\mathbb r^n$. we discuss inner products on nite dimensional real and complex. What Is The Standard Inner Product.
From www.youtube.com
Outer product vs inner product, and matrix representation of operator What Is The Standard Inner Product V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. an inner product is a generalization of the dot product. we discuss inner products on nite dimensional real and complex vector spaces. the dot product is the standard inner product on $\mathbb r^n$. an inner product on a vector space. What Is The Standard Inner Product.
From www.slideserve.com
PPT 8.1. Inner Product Spaces PowerPoint Presentation, free download What Is The Standard Inner Product V v !f satisfying (i) hv;vi 0, with equality if and only if v= 0 (ii)linearity. we discuss inner products on nite dimensional real and complex vector spaces. the dot product is the standard inner product on $\mathbb r^n$. We define the standard inner product on r^n and explain its. given an inner product \(\langle\),\(\rangle on \mathbb{r}^n\),. What Is The Standard Inner Product.
From www.slideserve.com
PPT Quantum Computation PowerPoint Presentation, free download ID What Is The Standard Inner Product an inner product on a vector space v over f is a function h;i: In general, any symmetric, positive definite. We define the standard inner product on r^n and explain its. we discuss inner products on nite dimensional real and complex vector spaces. an inner product is a generalization of the dot product. Although we are mainly. What Is The Standard Inner Product.
From www.slideserve.com
PPT Chapter 3 Linear Algebra Review and Elementary Differential What Is The Standard Inner Product We define the standard inner product on r^n and explain its. an inner product on a vector space v over f is a function h;i: we discuss inner products on nite dimensional real and complex vector spaces. In a vector space, it is a way to multiply vectors. In general, any symmetric, positive definite. Although we are mainly. What Is The Standard Inner Product.