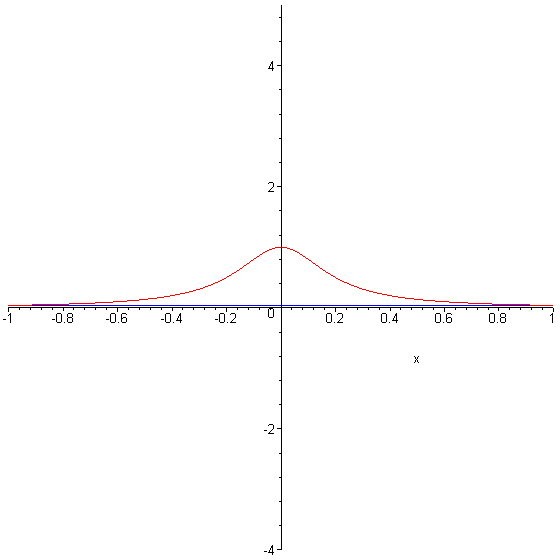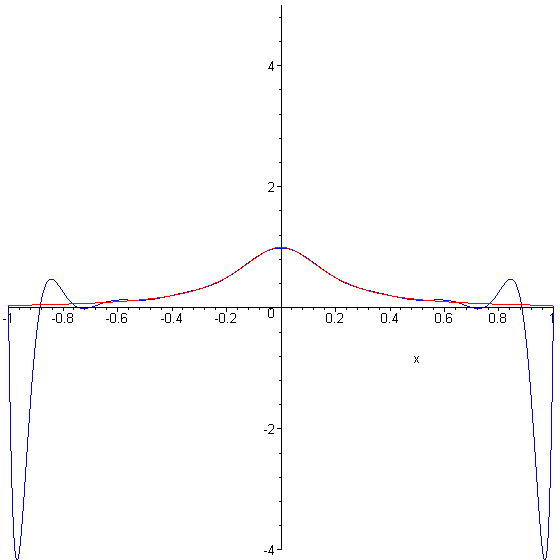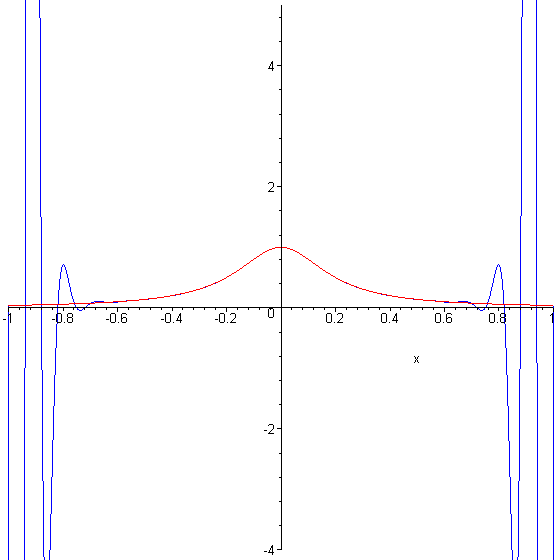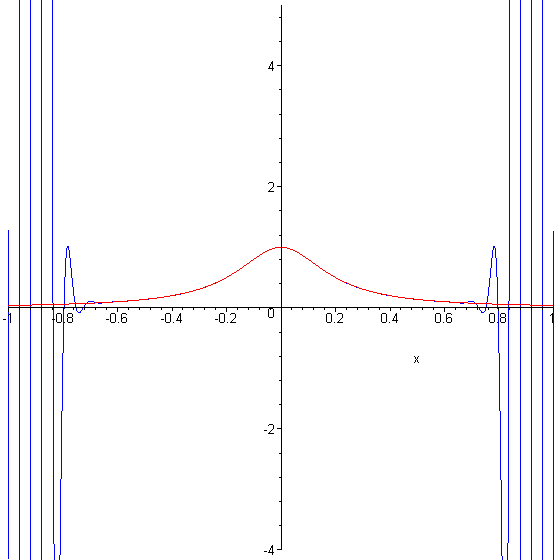
Runge S Phenomenon . Runge's phenomenon refers to the problem of oscillation that occurs when using polynomial interpolation to approximate a function,. In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using. Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. (compiled 16 august 2017) in this lecture we consider the dangers of. To combat this, we can use a. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. The runge phenomenon and piecewise polynomial interpolation.
from ece.uwaterloo.ca
To combat this, we can use a. In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. (compiled 16 august 2017) in this lecture we consider the dangers of. Runge's phenomenon refers to the problem of oscillation that occurs when using polynomial interpolation to approximate a function,. Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. The runge phenomenon and piecewise polynomial interpolation.
5.5 Polynomial Wiggle Department of Electrical and Computer
Runge S Phenomenon (compiled 16 august 2017) in this lecture we consider the dangers of. In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using. Runge's phenomenon refers to the problem of oscillation that occurs when using polynomial interpolation to approximate a function,. The runge phenomenon and piecewise polynomial interpolation. To combat this, we can use a. Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. (compiled 16 august 2017) in this lecture we consider the dangers of. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced.
From www.slideserve.com
PPT Introduction to Computer Vision and Robotics Motion Generation Runge S Phenomenon To combat this, we can use a. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. Runge's phenomenon refers to the problem of oscillation that occurs when using polynomial interpolation to approximate a function,. (compiled 16. Runge S Phenomenon.
From github.com
GitHub fan2fan/matlabInterpolationRungePhenomenon a program about Runge S Phenomenon In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using. The runge phenomenon and piecewise polynomial interpolation. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points. Runge S Phenomenon.
From mathepedia.de
Runges Phänomen Mathepedia Runge S Phenomenon Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using. Runge's phenomenon refers to the problem of oscillation that occurs when using polynomial interpolation to approximate a. Runge S Phenomenon.
From handwiki.org
Runge's phenomenon HandWiki Runge S Phenomenon In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using. (compiled 16 august 2017) in this lecture we consider the dangers of. The runge phenomenon and piecewise polynomial interpolation. Runge's phenomenon refers to the problem of oscillation that occurs when using polynomial interpolation to approximate a. Runge S Phenomenon.
From www.researchgate.net
Runge's phenomenon dash curveLIP and solid curveCIP Download Runge S Phenomenon The runge phenomenon and piecewise polynomial interpolation. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval. Runge S Phenomenon.
From www.youtube.com
Week 9 Lecture 44 Polynomial Interpolation Runge Phenomenon Runge S Phenomenon The runge phenomenon and piecewise polynomial interpolation. Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. In. Runge S Phenomenon.
From www.scribd.com
Runge Phenomenon Guided By Dr. Geetanjali Pradhan PDF Spline Runge S Phenomenon The runge phenomenon and piecewise polynomial interpolation. Runge's phenomenon refers to the problem of oscillation that occurs when using polynomial interpolation to approximate a function,. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. Because of. Runge S Phenomenon.
From www.researchgate.net
The function g from Example 4 exhibits the Runge phenomenon . Shown are Runge S Phenomenon This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using. The runge phenomenon. Runge S Phenomenon.
From zhuanlan.zhihu.com
龙格现象(Runge Phenomenon) 知乎 Runge S Phenomenon In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using. Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. Runge's phenomenon refers to the problem of oscillation that occurs when using polynomial interpolation to approximate a. Runge S Phenomenon.
From ayazhafiz.com
Approximation With Interpolating Polynomials Runge S Phenomenon Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using. The runge phenomenon and piecewise polynomial interpolation. To combat this, we can use a. (compiled 16 august. Runge S Phenomenon.
From www.researchgate.net
The presence of Runge's phenomenon Download Scientific Diagram Runge S Phenomenon (compiled 16 august 2017) in this lecture we consider the dangers of. The runge phenomenon and piecewise polynomial interpolation. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. In the mathematical field of numerical analysis, runge's. Runge S Phenomenon.
From github.com
GitHub vladchebotarev/Rungephenomenon The program in C Runge S Phenomenon Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. (compiled 16 august 2017) in this lecture we. Runge S Phenomenon.
From www.researchgate.net
The function g from Example 4 exhibits the Runge phenomenon . Shown are Runge S Phenomenon (compiled 16 august 2017) in this lecture we consider the dangers of. The runge phenomenon and piecewise polynomial interpolation. Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. To combat this, we can use a. Runge's phenomenon refers to the problem of oscillation that occurs when using polynomial interpolation to. Runge S Phenomenon.
From www.researchgate.net
Runge phenomenon. The grey stripes represent sensor length. Lower Runge S Phenomenon Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. The runge phenomenon and piecewise polynomial interpolation. Runge's. Runge S Phenomenon.
From www.youtube.com
Runge's Phenomenon YouTube Runge S Phenomenon Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. The runge phenomenon and piecewise polynomial interpolation. To combat this, we can use a. (compiled 16 august 2017) in this lecture we consider the dangers of. In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at. Runge S Phenomenon.
From www.researchgate.net
Runge phenomenon. The grey stripes represent sensor length. Lower Runge S Phenomenon Runge's phenomenon refers to the problem of oscillation that occurs when using polynomial interpolation to approximate a function,. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. To combat this, we can use a. Because of. Runge S Phenomenon.
From www.researchgate.net
Runge's function interpolated on an equispaced grid exhibiting Runge Runge S Phenomenon In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using. The runge phenomenon and piecewise polynomial interpolation. Runge's phenomenon refers to the problem of oscillation that occurs when using polynomial interpolation to approximate a function,. To combat this, we can use a. This is known as. Runge S Phenomenon.
From econopunk.com
rungephenomenon ed hori3 sh Econopunk Runge S Phenomenon (compiled 16 august 2017) in this lecture we consider the dangers of. Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. To combat this, we can use a. The runge phenomenon and piecewise polynomial interpolation. This is known as runge's phenomenon and mainly occurs at the endges of an interval. Runge S Phenomenon.
From ece.uwaterloo.ca
5.5 Polynomial Wiggle Department of Electrical and Computer Runge S Phenomenon Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. Runge's phenomenon refers to the problem of oscillation. Runge S Phenomenon.
From www.researchgate.net
Polynomial curve fitting and overfitting with Runge’s phenomenon. The Runge S Phenomenon The runge phenomenon and piecewise polynomial interpolation. In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using. (compiled 16 august 2017) in this lecture we consider the dangers of. To combat this, we can use a. Runge's phenomenon refers to the problem of oscillation that occurs. Runge S Phenomenon.
From www.researchgate.net
Comparison of Runge phenomenon of polynomial function with Gegenbauer Runge S Phenomenon To combat this, we can use a. Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. Runge's phenomenon refers to the problem of oscillation that occurs when using polynomial interpolation to approximate a function,. This is known as runge's phenomenon and mainly occurs at the endges of an interval when. Runge S Phenomenon.
From fr-academic.com
Phenomene de Runge Runge S Phenomenon This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. The runge phenomenon and piecewise polynomial interpolation. Runge's phenomenon refers to the problem of oscillation that occurs when using polynomial interpolation to approximate a function,. To combat. Runge S Phenomenon.
From www.researchgate.net
Runge phenomena, (a) Runge function with 10thorder polynomial Runge S Phenomenon Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. To combat this, we can use a. In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using. (compiled 16 august 2017) in this lecture we consider the. Runge S Phenomenon.
From www.semanticscholar.org
Runge's phenomenon Semantic Scholar Runge S Phenomenon The runge phenomenon and piecewise polynomial interpolation. In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points. Runge S Phenomenon.
From www.researchgate.net
Demonstration of Runge's phenomenon for y = 1 1+25x 2 , x ∈ [−1, 1 Runge S Phenomenon In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. To combat this,. Runge S Phenomenon.
From www.scribd.com
Interpolation With Higher Order Polynomials Is Prone To The Runge Runge S Phenomenon This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. Runge's phenomenon refers to the problem of oscillation. Runge S Phenomenon.
From www.semanticscholar.org
[PDF] Divergence (Runge Phenomenon) for leastsquares polynomial Runge S Phenomenon This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. Runge's phenomenon refers to the problem of oscillation that occurs when using polynomial interpolation to approximate a function,. The runge phenomenon and piecewise polynomial interpolation. Because of. Runge S Phenomenon.
From www.youtube.com
Runge's Phenomenon M3.11 Intro to DG YouTube Runge S Phenomenon To combat this, we can use a. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. (compiled. Runge S Phenomenon.
From www.researchgate.net
Runge's function interpolated on an equispaced grid exhibiting Runge Runge S Phenomenon To combat this, we can use a. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval. Runge S Phenomenon.
From www.researchgate.net
Runge's phenomenon dash curveLIP and solid curveCIP Download Runge S Phenomenon Runge's phenomenon refers to the problem of oscillation that occurs when using polynomial interpolation to approximate a function,. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. In the mathematical field of numerical analysis, runge's phenomenon. Runge S Phenomenon.
From slideplayer.com
Lecture 17 Polynomial interpolation. Runge example. Download rungepoly Runge S Phenomenon (compiled 16 august 2017) in this lecture we consider the dangers of. In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree. Runge S Phenomenon.
From math.stackexchange.com
numerical methods how to judge and analyze the convergence region Runge S Phenomenon In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using. To combat this, we can use a. The runge phenomenon and piecewise polynomial interpolation. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of. Runge S Phenomenon.
From www.researchgate.net
Comparison of Runge phenomenon in different cardinal functions. C(x) is Runge S Phenomenon To combat this, we can use a. Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. In. Runge S Phenomenon.
From www.semanticscholar.org
[PDF] Divergence (Runge Phenomenon) for leastsquares polynomial Runge S Phenomenon In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using. Because of runge's phenomenon, it is often the case that going to higher degrees does not always improve accuracy. Runge's phenomenon refers to the problem of oscillation that occurs when using polynomial interpolation to approximate a. Runge S Phenomenon.
From www.youtube.com
Lecture 163 Interpolation (Runge Phenomenon) YouTube Runge S Phenomenon The runge phenomenon and piecewise polynomial interpolation. This is known as runge's phenomenon and mainly occurs at the endges of an interval when using polynomial interpolation with polynomials of high degree over a set of points that are equally spaced. In the mathematical field of numerical analysis, runge's phenomenon is a problem of oscillation at the edges of an interval. Runge S Phenomenon.