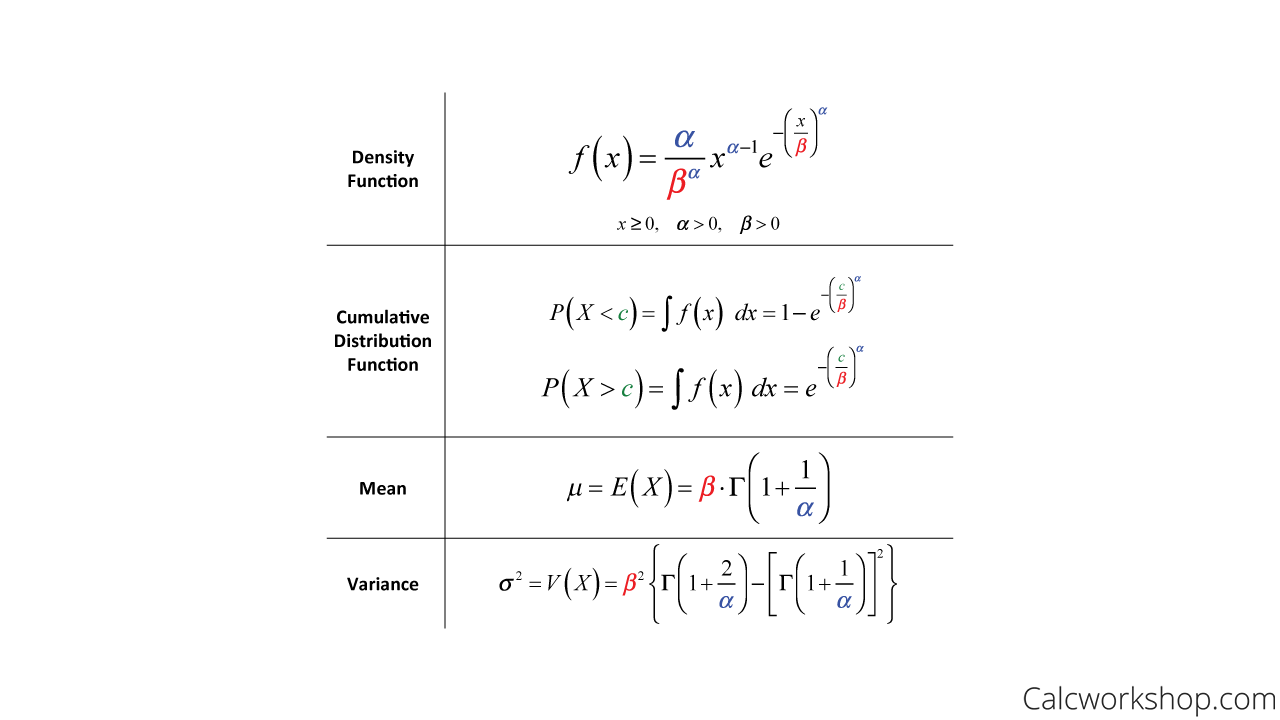
Mean Time Between Failure Weibull . Describes the use of the weibull distribution to calculate the mean time to failure (mttf) and mean time between failures. Depending on the value of the shape parameter. Mttf = η ∗ γ(1 +1/β) where γ is the gamma function The terms mtbf (mean time between failures) and mttf (mean time to failure) have often been interchangeably used to describe the average time to failure. The relationship between the slope and generic failure classes is discussed in section 1.7 and chapter 2. The characteristic life, η, is the. When \(\gamma\) = 1, the weibull reduces to the exponential model, with \(\alpha = 1/\lambda\) = the mean time to fail (mttf). Mean time to failure (mttf): The mttf for a weibull distribution can be calculated using the following formula: Otherwise, if β > 1, mttf will be less than.
from calcworkshop.com
The relationship between the slope and generic failure classes is discussed in section 1.7 and chapter 2. Mean time to failure (mttf): When \(\gamma\) = 1, the weibull reduces to the exponential model, with \(\alpha = 1/\lambda\) = the mean time to fail (mttf). Describes the use of the weibull distribution to calculate the mean time to failure (mttf) and mean time between failures. The characteristic life, η, is the. Otherwise, if β > 1, mttf will be less than. Mttf = η ∗ γ(1 +1/β) where γ is the gamma function Depending on the value of the shape parameter. The terms mtbf (mean time between failures) and mttf (mean time to failure) have often been interchangeably used to describe the average time to failure. The mttf for a weibull distribution can be calculated using the following formula:
Weibull & Lognormal Distribution (with 7 Examples!)
Mean Time Between Failure Weibull When \(\gamma\) = 1, the weibull reduces to the exponential model, with \(\alpha = 1/\lambda\) = the mean time to fail (mttf). The terms mtbf (mean time between failures) and mttf (mean time to failure) have often been interchangeably used to describe the average time to failure. Depending on the value of the shape parameter. The mttf for a weibull distribution can be calculated using the following formula: Otherwise, if β > 1, mttf will be less than. The characteristic life, η, is the. Mean time to failure (mttf): When \(\gamma\) = 1, the weibull reduces to the exponential model, with \(\alpha = 1/\lambda\) = the mean time to fail (mttf). Describes the use of the weibull distribution to calculate the mean time to failure (mttf) and mean time between failures. Mttf = η ∗ γ(1 +1/β) where γ is the gamma function The relationship between the slope and generic failure classes is discussed in section 1.7 and chapter 2.
From support.sas.com
Weibull Probability Plot for Two Combined Failure Modes SAS/QC(R) 13 Mean Time Between Failure Weibull Mean time to failure (mttf): Describes the use of the weibull distribution to calculate the mean time to failure (mttf) and mean time between failures. Mttf = η ∗ γ(1 +1/β) where γ is the gamma function The characteristic life, η, is the. Otherwise, if β > 1, mttf will be less than. When \(\gamma\) = 1, the weibull reduces. Mean Time Between Failure Weibull.
From www.researchgate.net
Weibull probability plot of failure times (see online version for Mean Time Between Failure Weibull Otherwise, if β > 1, mttf will be less than. Mttf = η ∗ γ(1 +1/β) where γ is the gamma function The terms mtbf (mean time between failures) and mttf (mean time to failure) have often been interchangeably used to describe the average time to failure. The characteristic life, η, is the. Mean time to failure (mttf): Describes the. Mean Time Between Failure Weibull.
From www.researchgate.net
Time to failure of the Weibull distribution of tree model 1(divided by Mean Time Between Failure Weibull The mttf for a weibull distribution can be calculated using the following formula: When \(\gamma\) = 1, the weibull reduces to the exponential model, with \(\alpha = 1/\lambda\) = the mean time to fail (mttf). Otherwise, if β > 1, mttf will be less than. Mean time to failure (mttf): Describes the use of the weibull distribution to calculate the. Mean Time Between Failure Weibull.
From calcworkshop.com
Weibull & Lognormal Distribution (with 7 Examples!) Mean Time Between Failure Weibull When \(\gamma\) = 1, the weibull reduces to the exponential model, with \(\alpha = 1/\lambda\) = the mean time to fail (mttf). Depending on the value of the shape parameter. The characteristic life, η, is the. The mttf for a weibull distribution can be calculated using the following formula: The terms mtbf (mean time between failures) and mttf (mean time. Mean Time Between Failure Weibull.
From www.researchgate.net
Weibull probability plot displaying time to failure across study groups Mean Time Between Failure Weibull The relationship between the slope and generic failure classes is discussed in section 1.7 and chapter 2. Mean time to failure (mttf): Describes the use of the weibull distribution to calculate the mean time to failure (mttf) and mean time between failures. Otherwise, if β > 1, mttf will be less than. Mttf = η ∗ γ(1 +1/β) where γ. Mean Time Between Failure Weibull.
From www.researchgate.net
Weibull failure probability plot for observed data Download Mean Time Between Failure Weibull The relationship between the slope and generic failure classes is discussed in section 1.7 and chapter 2. The terms mtbf (mean time between failures) and mttf (mean time to failure) have often been interchangeably used to describe the average time to failure. Describes the use of the weibull distribution to calculate the mean time to failure (mttf) and mean time. Mean Time Between Failure Weibull.
From www.researchgate.net
(PDF) Study on Mean Time Between Failures Prediction Algorithms Based Mean Time Between Failure Weibull Mttf = η ∗ γ(1 +1/β) where γ is the gamma function Mean time to failure (mttf): The relationship between the slope and generic failure classes is discussed in section 1.7 and chapter 2. The mttf for a weibull distribution can be calculated using the following formula: The characteristic life, η, is the. When \(\gamma\) = 1, the weibull reduces. Mean Time Between Failure Weibull.
From www.researchgate.net
(PDF) Using Weibull accelerated failure time regression model to Mean Time Between Failure Weibull The mttf for a weibull distribution can be calculated using the following formula: Describes the use of the weibull distribution to calculate the mean time to failure (mttf) and mean time between failures. Depending on the value of the shape parameter. Mean time to failure (mttf): Mttf = η ∗ γ(1 +1/β) where γ is the gamma function When \(\gamma\). Mean Time Between Failure Weibull.
From demonstrations.wolfram.com
Fitting TimestoFailure to a Weibull Distribution Wolfram Mean Time Between Failure Weibull The characteristic life, η, is the. Mttf = η ∗ γ(1 +1/β) where γ is the gamma function Mean time to failure (mttf): Otherwise, if β > 1, mttf will be less than. The relationship between the slope and generic failure classes is discussed in section 1.7 and chapter 2. Describes the use of the weibull distribution to calculate the. Mean Time Between Failure Weibull.
From slideplayer.com
Wan Mohd Faizal Bin Wan Abd Rahim ppt download Mean Time Between Failure Weibull Mean time to failure (mttf): Mttf = η ∗ γ(1 +1/β) where γ is the gamma function Otherwise, if β > 1, mttf will be less than. Depending on the value of the shape parameter. The terms mtbf (mean time between failures) and mttf (mean time to failure) have often been interchangeably used to describe the average time to failure.. Mean Time Between Failure Weibull.
From www.researchgate.net
Time to failure of the Weibull distribution of tree model 2(divided by Mean Time Between Failure Weibull The relationship between the slope and generic failure classes is discussed in section 1.7 and chapter 2. The mttf for a weibull distribution can be calculated using the following formula: When \(\gamma\) = 1, the weibull reduces to the exponential model, with \(\alpha = 1/\lambda\) = the mean time to fail (mttf). The terms mtbf (mean time between failures) and. Mean Time Between Failure Weibull.
From www.researchgate.net
The Weibull Probability Plot for Failure times for Wear Depth Mean Time Between Failure Weibull The characteristic life, η, is the. Describes the use of the weibull distribution to calculate the mean time to failure (mttf) and mean time between failures. Mttf = η ∗ γ(1 +1/β) where γ is the gamma function When \(\gamma\) = 1, the weibull reduces to the exponential model, with \(\alpha = 1/\lambda\) = the mean time to fail (mttf).. Mean Time Between Failure Weibull.
From www.windpowerengineering.com
Weibull analysis applied to wind projects Mean Time Between Failure Weibull The characteristic life, η, is the. When \(\gamma\) = 1, the weibull reduces to the exponential model, with \(\alpha = 1/\lambda\) = the mean time to fail (mttf). Mttf = η ∗ γ(1 +1/β) where γ is the gamma function Otherwise, if β > 1, mttf will be less than. The mttf for a weibull distribution can be calculated using. Mean Time Between Failure Weibull.
From ar.inspiredpencil.com
Weibull Failure Rate Mean Time Between Failure Weibull The relationship between the slope and generic failure classes is discussed in section 1.7 and chapter 2. Mttf = η ∗ γ(1 +1/β) where γ is the gamma function The characteristic life, η, is the. Describes the use of the weibull distribution to calculate the mean time to failure (mttf) and mean time between failures. When \(\gamma\) = 1, the. Mean Time Between Failure Weibull.
From ar.inspiredpencil.com
Weibull Failure Rate Mean Time Between Failure Weibull Describes the use of the weibull distribution to calculate the mean time to failure (mttf) and mean time between failures. The characteristic life, η, is the. Depending on the value of the shape parameter. Mttf = η ∗ γ(1 +1/β) where γ is the gamma function Otherwise, if β > 1, mttf will be less than. Mean time to failure. Mean Time Between Failure Weibull.
From www.researchgate.net
Weibull probability distribution of failure strength for different Mean Time Between Failure Weibull When \(\gamma\) = 1, the weibull reduces to the exponential model, with \(\alpha = 1/\lambda\) = the mean time to fail (mttf). Otherwise, if β > 1, mttf will be less than. The characteristic life, η, is the. The mttf for a weibull distribution can be calculated using the following formula: The relationship between the slope and generic failure classes. Mean Time Between Failure Weibull.
From www.researchgate.net
Weibull probability plot of number of cycles to failure (NOC Mean Time Between Failure Weibull The relationship between the slope and generic failure classes is discussed in section 1.7 and chapter 2. Mttf = η ∗ γ(1 +1/β) where γ is the gamma function Otherwise, if β > 1, mttf will be less than. Depending on the value of the shape parameter. The mttf for a weibull distribution can be calculated using the following formula:. Mean Time Between Failure Weibull.
From www.slideserve.com
PPT Reliability Application PowerPoint Presentation, free download Mean Time Between Failure Weibull Mean time to failure (mttf): Mttf = η ∗ γ(1 +1/β) where γ is the gamma function Depending on the value of the shape parameter. The relationship between the slope and generic failure classes is discussed in section 1.7 and chapter 2. The terms mtbf (mean time between failures) and mttf (mean time to failure) have often been interchangeably used. Mean Time Between Failure Weibull.
From www.researchgate.net
The a) stress and b) timetofailure Weibull distribution functions Mean Time Between Failure Weibull Mean time to failure (mttf): The characteristic life, η, is the. Describes the use of the weibull distribution to calculate the mean time to failure (mttf) and mean time between failures. The terms mtbf (mean time between failures) and mttf (mean time to failure) have often been interchangeably used to describe the average time to failure. The mttf for a. Mean Time Between Failure Weibull.
From www.researchgate.net
Illustration of the effect of β on the Weibull failure rate curve over Mean Time Between Failure Weibull The terms mtbf (mean time between failures) and mttf (mean time to failure) have often been interchangeably used to describe the average time to failure. Otherwise, if β > 1, mttf will be less than. The mttf for a weibull distribution can be calculated using the following formula: The relationship between the slope and generic failure classes is discussed in. Mean Time Between Failure Weibull.
From calcworkshop.com
Weibull & Lognormal Distribution (with 7 Examples!) Mean Time Between Failure Weibull The characteristic life, η, is the. Describes the use of the weibull distribution to calculate the mean time to failure (mttf) and mean time between failures. The terms mtbf (mean time between failures) and mttf (mean time to failure) have often been interchangeably used to describe the average time to failure. When \(\gamma\) = 1, the weibull reduces to the. Mean Time Between Failure Weibull.
From www.researchgate.net
A Weibull probability plot showing ML estimates for the failure time Mean Time Between Failure Weibull Mttf = η ∗ γ(1 +1/β) where γ is the gamma function Mean time to failure (mttf): When \(\gamma\) = 1, the weibull reduces to the exponential model, with \(\alpha = 1/\lambda\) = the mean time to fail (mttf). The relationship between the slope and generic failure classes is discussed in section 1.7 and chapter 2. Otherwise, if β >. Mean Time Between Failure Weibull.
From www.researchgate.net
Weibull probability plot of time to failure for the study groups Mean Time Between Failure Weibull The mttf for a weibull distribution can be calculated using the following formula: The terms mtbf (mean time between failures) and mttf (mean time to failure) have often been interchangeably used to describe the average time to failure. Depending on the value of the shape parameter. Describes the use of the weibull distribution to calculate the mean time to failure. Mean Time Between Failure Weibull.
From integraoptics.com
What’s Up with Mean Time Between Failure Integra Optics Mean Time Between Failure Weibull Mean time to failure (mttf): The terms mtbf (mean time between failures) and mttf (mean time to failure) have often been interchangeably used to describe the average time to failure. When \(\gamma\) = 1, the weibull reduces to the exponential model, with \(\alpha = 1/\lambda\) = the mean time to fail (mttf). Otherwise, if β > 1, mttf will be. Mean Time Between Failure Weibull.
From www.researchgate.net
Weibull probability plot of time to failure for the study groups Mean Time Between Failure Weibull The relationship between the slope and generic failure classes is discussed in section 1.7 and chapter 2. The characteristic life, η, is the. Describes the use of the weibull distribution to calculate the mean time to failure (mttf) and mean time between failures. Otherwise, if β > 1, mttf will be less than. Mttf = η ∗ γ(1 +1/β) where. Mean Time Between Failure Weibull.
From www.academia.edu
(PDF) Analisis reliability remunerasi.uns.ac.id dengan mean time Mean Time Between Failure Weibull The mttf for a weibull distribution can be calculated using the following formula: The characteristic life, η, is the. Mttf = η ∗ γ(1 +1/β) where γ is the gamma function Otherwise, if β > 1, mttf will be less than. Depending on the value of the shape parameter. The relationship between the slope and generic failure classes is discussed. Mean Time Between Failure Weibull.
From ieeexplore.ieee.org
An interval estimate of meantimetofailure for a product with Mean Time Between Failure Weibull The mttf for a weibull distribution can be calculated using the following formula: The characteristic life, η, is the. Otherwise, if β > 1, mttf will be less than. Depending on the value of the shape parameter. Mttf = η ∗ γ(1 +1/β) where γ is the gamma function The terms mtbf (mean time between failures) and mttf (mean time. Mean Time Between Failure Weibull.
From www.researchgate.net
Weibull probability of failure as a function of time to breakdown Mean Time Between Failure Weibull The mttf for a weibull distribution can be calculated using the following formula: The relationship between the slope and generic failure classes is discussed in section 1.7 and chapter 2. Otherwise, if β > 1, mttf will be less than. When \(\gamma\) = 1, the weibull reduces to the exponential model, with \(\alpha = 1/\lambda\) = the mean time to. Mean Time Between Failure Weibull.
From www.researchgate.net
Weibull probability plot of time to failure for the specimens aged at Mean Time Between Failure Weibull The mttf for a weibull distribution can be calculated using the following formula: The terms mtbf (mean time between failures) and mttf (mean time to failure) have often been interchangeably used to describe the average time to failure. The relationship between the slope and generic failure classes is discussed in section 1.7 and chapter 2. Otherwise, if β > 1,. Mean Time Between Failure Weibull.
From relyence.com
An Introduction to Weibull Analysis Mean Time Between Failure Weibull The terms mtbf (mean time between failures) and mttf (mean time to failure) have often been interchangeably used to describe the average time to failure. Mttf = η ∗ γ(1 +1/β) where γ is the gamma function Mean time to failure (mttf): Depending on the value of the shape parameter. When \(\gamma\) = 1, the weibull reduces to the exponential. Mean Time Between Failure Weibull.
From www.researchgate.net
Weibull probability plot of Time To Failure for MC68HC908SR12CFA with Mean Time Between Failure Weibull The terms mtbf (mean time between failures) and mttf (mean time to failure) have often been interchangeably used to describe the average time to failure. Mean time to failure (mttf): The characteristic life, η, is the. Mttf = η ∗ γ(1 +1/β) where γ is the gamma function Depending on the value of the shape parameter. Describes the use of. Mean Time Between Failure Weibull.
From www.researchgate.net
A Weibull accelerated failure time models of PFS Download Table Mean Time Between Failure Weibull Describes the use of the weibull distribution to calculate the mean time to failure (mttf) and mean time between failures. The mttf for a weibull distribution can be calculated using the following formula: The relationship between the slope and generic failure classes is discussed in section 1.7 and chapter 2. Mean time to failure (mttf): When \(\gamma\) = 1, the. Mean Time Between Failure Weibull.
From www.windpowerengineering.com
Weibull analysis applied to wind projects Mean Time Between Failure Weibull Otherwise, if β > 1, mttf will be less than. The relationship between the slope and generic failure classes is discussed in section 1.7 and chapter 2. Mttf = η ∗ γ(1 +1/β) where γ is the gamma function Describes the use of the weibull distribution to calculate the mean time to failure (mttf) and mean time between failures. The. Mean Time Between Failure Weibull.
From www.allaboutcircuits.com
How the Weibull Distribution Is Used in Reliability Engineering Mean Time Between Failure Weibull The terms mtbf (mean time between failures) and mttf (mean time to failure) have often been interchangeably used to describe the average time to failure. When \(\gamma\) = 1, the weibull reduces to the exponential model, with \(\alpha = 1/\lambda\) = the mean time to fail (mttf). Mttf = η ∗ γ(1 +1/β) where γ is the gamma function Depending. Mean Time Between Failure Weibull.
From www.researchgate.net
8 Weibull curve (bathtub curve) for failure rate over time. Download Mean Time Between Failure Weibull The characteristic life, η, is the. Mean time to failure (mttf): When \(\gamma\) = 1, the weibull reduces to the exponential model, with \(\alpha = 1/\lambda\) = the mean time to fail (mttf). The terms mtbf (mean time between failures) and mttf (mean time to failure) have often been interchangeably used to describe the average time to failure. The mttf. Mean Time Between Failure Weibull.