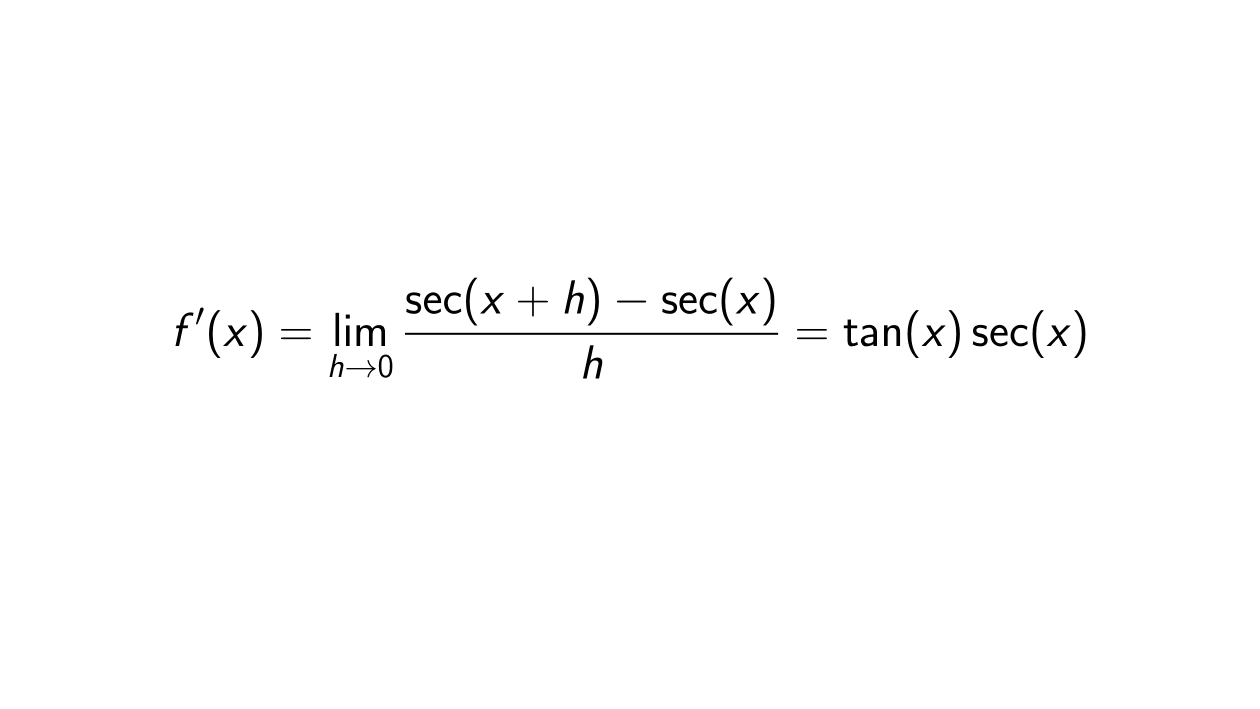Is Sec X Continuous . No, the function \(f(x) = \sec x\) is not continuous everywhere. No, the function f (x) = sec x is not continuous on the interval [− π 2, π 2] because the function is undefined at x = − π 2 and. It is discontinuous at the points \(x = (2n+1)\frac{\pi}{2}\), for any integer value of n. When we introduced the exponential function f(x)= bx in section 0.5, we. Let f (x) = sec x. How are you defining $\sec x$ at the exceptional points? The functions sin x and cos x are continuous at all real numbers. It is not sensible to say a function is not continuous where it is not defined. And cos x = 0 when, x = π 2 π 2 and odd multiples of π 2 π 2 like − π 2 − π 2. Therefore, f (x) = 1 cosx 1 c o s x. The absolute value function |x| is continuous over the set of all real numbers. Metric functions defined in section 0.4 is continuous at each point of its domain. F (x) is not defined when cos x = 0. For certain values of x, the tangent, cotangent, secant and cosecant curves are not defined, and so there is a gap in the curve. [for more on this topic, go to continuous and discontinuous functions in an.
from www.epsilonify.com
How are you defining $\sec x$ at the exceptional points? Metric functions defined in section 0.4 is continuous at each point of its domain. Let f (x) = sec x. It is not sensible to say a function is not continuous where it is not defined. Exponential functions are continuous at all real numbers. [for more on this topic, go to continuous and discontinuous functions in an. No, the function f (x) = sec x is not continuous on the interval [− π 2, π 2] because the function is undefined at x = − π 2 and. No, the function \(f(x) = \sec x\) is not continuous everywhere. And cos x = 0 when, x = π 2 π 2 and odd multiples of π 2 π 2 like − π 2 − π 2. When we introduced the exponential function f(x)= bx in section 0.5, we.
Derivative of sec(x) using First Principle of Derivative Epsilonify
Is Sec X Continuous When we introduced the exponential function f(x)= bx in section 0.5, we. Let f (x) = sec x. Therefore, f (x) = 1 cosx 1 c o s x. It is not sensible to say a function is not continuous where it is not defined. It is discontinuous at the points \(x = (2n+1)\frac{\pi}{2}\), for any integer value of n. When we introduced the exponential function f(x)= bx in section 0.5, we. The functions sin x and cos x are continuous at all real numbers. [for more on this topic, go to continuous and discontinuous functions in an. How are you defining $\sec x$ at the exceptional points? The absolute value function |x| is continuous over the set of all real numbers. For certain values of x, the tangent, cotangent, secant and cosecant curves are not defined, and so there is a gap in the curve. Metric functions defined in section 0.4 is continuous at each point of its domain. F (x) is not defined when cos x = 0. No, the function \(f(x) = \sec x\) is not continuous everywhere. No, the function f (x) = sec x is not continuous on the interval [− π 2, π 2] because the function is undefined at x = − π 2 and. And cos x = 0 when, x = π 2 π 2 and odd multiples of π 2 π 2 like − π 2 − π 2.
From www.youtube.com
graph of secx YouTube Is Sec X Continuous How are you defining $\sec x$ at the exceptional points? The absolute value function |x| is continuous over the set of all real numbers. It is discontinuous at the points \(x = (2n+1)\frac{\pi}{2}\), for any integer value of n. Exponential functions are continuous at all real numbers. F (x) is not defined when cos x = 0. And cos x. Is Sec X Continuous.
From etc.usf.edu
Secant and Cosecant Curves, y=sec x and y=csc x ClipArt ETC Is Sec X Continuous For certain values of x, the tangent, cotangent, secant and cosecant curves are not defined, and so there is a gap in the curve. It is discontinuous at the points \(x = (2n+1)\frac{\pi}{2}\), for any integer value of n. F (x) is not defined when cos x = 0. The functions sin x and cos x are continuous at all. Is Sec X Continuous.
From www.youtube.com
Graph of y = sec(x) YouTube Is Sec X Continuous No, the function \(f(x) = \sec x\) is not continuous everywhere. Let f (x) = sec x. For certain values of x, the tangent, cotangent, secant and cosecant curves are not defined, and so there is a gap in the curve. No, the function f (x) = sec x is not continuous on the interval [− π 2, π 2]. Is Sec X Continuous.
From www.youtube.com
Calculus What is a continuous function How to check if a log Is Sec X Continuous No, the function \(f(x) = \sec x\) is not continuous everywhere. For certain values of x, the tangent, cotangent, secant and cosecant curves are not defined, and so there is a gap in the curve. Therefore, f (x) = 1 cosx 1 c o s x. [for more on this topic, go to continuous and discontinuous functions in an. The. Is Sec X Continuous.
From www.youtube.com
Find the Limit of sec(x) as x approaches negative pi/2 from the left Is Sec X Continuous Therefore, f (x) = 1 cosx 1 c o s x. For certain values of x, the tangent, cotangent, secant and cosecant curves are not defined, and so there is a gap in the curve. Let f (x) = sec x. F (x) is not defined when cos x = 0. Exponential functions are continuous at all real numbers. No,. Is Sec X Continuous.
From www.youtube.com
Integral of sec x YouTube Is Sec X Continuous [for more on this topic, go to continuous and discontinuous functions in an. No, the function f (x) = sec x is not continuous on the interval [− π 2, π 2] because the function is undefined at x = − π 2 and. The absolute value function |x| is continuous over the set of all real numbers. And cos. Is Sec X Continuous.
From calcworkshop.com
Continuous Uniform Distribution (Defined w/ 5 Examples!) Is Sec X Continuous No, the function f (x) = sec x is not continuous on the interval [− π 2, π 2] because the function is undefined at x = − π 2 and. The functions sin x and cos x are continuous at all real numbers. When we introduced the exponential function f(x)= bx in section 0.5, we. F (x) is not. Is Sec X Continuous.
From www.youtube.com
Q58 Evaluate sec x dx Integral of sec x Integration of sec x Is Sec X Continuous It is discontinuous at the points \(x = (2n+1)\frac{\pi}{2}\), for any integer value of n. Let f (x) = sec x. [for more on this topic, go to continuous and discontinuous functions in an. And cos x = 0 when, x = π 2 π 2 and odd multiples of π 2 π 2 like − π 2 − π. Is Sec X Continuous.
From www.youtube.com
Indefinite Integral of sec(x) YouTube Is Sec X Continuous F (x) is not defined when cos x = 0. And cos x = 0 when, x = π 2 π 2 and odd multiples of π 2 π 2 like − π 2 − π 2. [for more on this topic, go to continuous and discontinuous functions in an. The functions sin x and cos x are continuous at. Is Sec X Continuous.
From www.youtube.com
Integration of secx Integral of secx secx Integration YouTube Is Sec X Continuous Let f (x) = sec x. Therefore, f (x) = 1 cosx 1 c o s x. Metric functions defined in section 0.4 is continuous at each point of its domain. It is not sensible to say a function is not continuous where it is not defined. Exponential functions are continuous at all real numbers. The functions sin x and. Is Sec X Continuous.
From www.youtube.com
Continuity Continuous Whether xsin(1/x) is continuous at 0 or not Is Sec X Continuous It is discontinuous at the points \(x = (2n+1)\frac{\pi}{2}\), for any integer value of n. No, the function \(f(x) = \sec x\) is not continuous everywhere. For certain values of x, the tangent, cotangent, secant and cosecant curves are not defined, and so there is a gap in the curve. Let f (x) = sec x. [for more on this. Is Sec X Continuous.
From slideplayer.com
Sec 2.5 Continuity Continuous Function ppt download Is Sec X Continuous For certain values of x, the tangent, cotangent, secant and cosecant curves are not defined, and so there is a gap in the curve. It is discontinuous at the points \(x = (2n+1)\frac{\pi}{2}\), for any integer value of n. Let f (x) = sec x. The absolute value function |x| is continuous over the set of all real numbers. The. Is Sec X Continuous.
From www.youtube.com
INVERSE TRIGONOMETRIC FUNCTIONS (sec) (6) ( Domain, Range and Graph Is Sec X Continuous Let f (x) = sec x. When we introduced the exponential function f(x)= bx in section 0.5, we. And cos x = 0 when, x = π 2 π 2 and odd multiples of π 2 π 2 like − π 2 − π 2. No, the function \(f(x) = \sec x\) is not continuous everywhere. It is discontinuous at. Is Sec X Continuous.
From www.youtube.com
How to graph y=sec(x) and y=csc(x) (with asymptotes, domain and range Is Sec X Continuous It is not sensible to say a function is not continuous where it is not defined. It is discontinuous at the points \(x = (2n+1)\frac{\pi}{2}\), for any integer value of n. The functions sin x and cos x are continuous at all real numbers. How are you defining $\sec x$ at the exceptional points? The absolute value function |x| is. Is Sec X Continuous.
From www.chegg.com
Solved Verify the identity by converting the left side into Is Sec X Continuous It is discontinuous at the points \(x = (2n+1)\frac{\pi}{2}\), for any integer value of n. Exponential functions are continuous at all real numbers. When we introduced the exponential function f(x)= bx in section 0.5, we. How are you defining $\sec x$ at the exceptional points? It is not sensible to say a function is not continuous where it is not. Is Sec X Continuous.
From www.youtube.com
Integral of e^(sec x) sec x tan x Integration of Trigonometric and Is Sec X Continuous It is not sensible to say a function is not continuous where it is not defined. The absolute value function |x| is continuous over the set of all real numbers. Metric functions defined in section 0.4 is continuous at each point of its domain. When we introduced the exponential function f(x)= bx in section 0.5, we. No, the function \(f(x). Is Sec X Continuous.
From www.coursehero.com
[Solved] Verify the identity. Sec x sec x sin x = cos x To verify Is Sec X Continuous When we introduced the exponential function f(x)= bx in section 0.5, we. [for more on this topic, go to continuous and discontinuous functions in an. The functions sin x and cos x are continuous at all real numbers. It is not sensible to say a function is not continuous where it is not defined. Exponential functions are continuous at all. Is Sec X Continuous.
From www.youtube.com
Q51 ∫secx/(secx+tanx) dx Integration of secx/(secx+tanx Is Sec X Continuous Metric functions defined in section 0.4 is continuous at each point of its domain. For certain values of x, the tangent, cotangent, secant and cosecant curves are not defined, and so there is a gap in the curve. When we introduced the exponential function f(x)= bx in section 0.5, we. Let f (x) = sec x. [for more on this. Is Sec X Continuous.
From www.studocu.com
Sec. 2.5 Continuity Math 181A Sec. 2. Continuity A function f is Is Sec X Continuous No, the function \(f(x) = \sec x\) is not continuous everywhere. Therefore, f (x) = 1 cosx 1 c o s x. Exponential functions are continuous at all real numbers. How are you defining $\sec x$ at the exceptional points? F (x) is not defined when cos x = 0. And cos x = 0 when, x = π 2. Is Sec X Continuous.
From www.youtube.com
Integration of ∫ (Sec x/Sec x + Tan x) dx YouTube Is Sec X Continuous And cos x = 0 when, x = π 2 π 2 and odd multiples of π 2 π 2 like − π 2 − π 2. F (x) is not defined when cos x = 0. The functions sin x and cos x are continuous at all real numbers. No, the function f (x) = sec x is not. Is Sec X Continuous.
From www.youtube.com
Graph of sec x Graph of Csc x Domain and Range Math 10 Lesson 05 Is Sec X Continuous Let f (x) = sec x. It is discontinuous at the points \(x = (2n+1)\frac{\pi}{2}\), for any integer value of n. When we introduced the exponential function f(x)= bx in section 0.5, we. F (x) is not defined when cos x = 0. How are you defining $\sec x$ at the exceptional points? Exponential functions are continuous at all real. Is Sec X Continuous.
From byjus.com
The range of sec 1 x is Is Sec X Continuous Metric functions defined in section 0.4 is continuous at each point of its domain. Let f (x) = sec x. The functions sin x and cos x are continuous at all real numbers. The absolute value function |x| is continuous over the set of all real numbers. F (x) is not defined when cos x = 0. For certain values. Is Sec X Continuous.
From todayworldinfo.com
Derivative of Secx Calculating the Derivative of Secx Is Sec X Continuous Therefore, f (x) = 1 cosx 1 c o s x. And cos x = 0 when, x = π 2 π 2 and odd multiples of π 2 π 2 like − π 2 − π 2. It is discontinuous at the points \(x = (2n+1)\frac{\pi}{2}\), for any integer value of n. No, the function \(f(x) = \sec x\). Is Sec X Continuous.
From www.cuemath.com
Secant Function Domain and Range Solved Examples Cuemath Is Sec X Continuous When we introduced the exponential function f(x)= bx in section 0.5, we. It is not sensible to say a function is not continuous where it is not defined. Metric functions defined in section 0.4 is continuous at each point of its domain. No, the function \(f(x) = \sec x\) is not continuous everywhere. The absolute value function |x| is continuous. Is Sec X Continuous.
From www.youtube.com
Trigonometric Identity Integral of sec(x) YouTube Is Sec X Continuous Exponential functions are continuous at all real numbers. It is not sensible to say a function is not continuous where it is not defined. And cos x = 0 when, x = π 2 π 2 and odd multiples of π 2 π 2 like − π 2 − π 2. Metric functions defined in section 0.4 is continuous at. Is Sec X Continuous.
From www.youtube.com
積分csc(x)sec(x) & sec(x); 怎樣可以用1=sin^2(x)+cos^2(x) YouTube Is Sec X Continuous It is not sensible to say a function is not continuous where it is not defined. It is discontinuous at the points \(x = (2n+1)\frac{\pi}{2}\), for any integer value of n. Exponential functions are continuous at all real numbers. When we introduced the exponential function f(x)= bx in section 0.5, we. Let f (x) = sec x. For certain values. Is Sec X Continuous.
From www.epsilonify.com
Derivative of sec(x) using First Principle of Derivative Epsilonify Is Sec X Continuous When we introduced the exponential function f(x)= bx in section 0.5, we. Therefore, f (x) = 1 cosx 1 c o s x. The absolute value function |x| is continuous over the set of all real numbers. For certain values of x, the tangent, cotangent, secant and cosecant curves are not defined, and so there is a gap in the. Is Sec X Continuous.
From slideplayer.com
Sec 2.5 Continuity Continuous Function ppt download Is Sec X Continuous How are you defining $\sec x$ at the exceptional points? The absolute value function |x| is continuous over the set of all real numbers. F (x) is not defined when cos x = 0. It is discontinuous at the points \(x = (2n+1)\frac{\pi}{2}\), for any integer value of n. The functions sin x and cos x are continuous at all. Is Sec X Continuous.
From testbook.com
Derivative of sec x Learn definition, formula, Proof & examples Is Sec X Continuous When we introduced the exponential function f(x)= bx in section 0.5, we. [for more on this topic, go to continuous and discontinuous functions in an. Metric functions defined in section 0.4 is continuous at each point of its domain. Therefore, f (x) = 1 cosx 1 c o s x. It is discontinuous at the points \(x = (2n+1)\frac{\pi}{2}\), for. Is Sec X Continuous.
From slideplayer.com
Sec 2.5 Continuity Continuous Function ppt download Is Sec X Continuous Let f (x) = sec x. Metric functions defined in section 0.4 is continuous at each point of its domain. And cos x = 0 when, x = π 2 π 2 and odd multiples of π 2 π 2 like − π 2 − π 2. It is not sensible to say a function is not continuous where it. Is Sec X Continuous.
From www.youtube.com
Where is The Function f(x) = sec x Continuous YouTube Is Sec X Continuous For certain values of x, the tangent, cotangent, secant and cosecant curves are not defined, and so there is a gap in the curve. [for more on this topic, go to continuous and discontinuous functions in an. Metric functions defined in section 0.4 is continuous at each point of its domain. It is discontinuous at the points \(x = (2n+1)\frac{\pi}{2}\),. Is Sec X Continuous.
From www.analyzemath.com
Secant Function sec x Is Sec X Continuous No, the function f (x) = sec x is not continuous on the interval [− π 2, π 2] because the function is undefined at x = − π 2 and. It is discontinuous at the points \(x = (2n+1)\frac{\pi}{2}\), for any integer value of n. And cos x = 0 when, x = π 2 π 2 and odd. Is Sec X Continuous.
From www.youtube.com
What is Secant and How to Graph y=sec x YouTube Is Sec X Continuous Exponential functions are continuous at all real numbers. It is not sensible to say a function is not continuous where it is not defined. When we introduced the exponential function f(x)= bx in section 0.5, we. It is discontinuous at the points \(x = (2n+1)\frac{\pi}{2}\), for any integer value of n. How are you defining $\sec x$ at the exceptional. Is Sec X Continuous.
From peakd.com
Trigonometry Derivative of sec(x) Proof PeakD Is Sec X Continuous Therefore, f (x) = 1 cosx 1 c o s x. No, the function \(f(x) = \sec x\) is not continuous everywhere. [for more on this topic, go to continuous and discontinuous functions in an. Metric functions defined in section 0.4 is continuous at each point of its domain. Exponential functions are continuous at all real numbers. No, the function. Is Sec X Continuous.
From www.youtube.com
Graph y=sec(x) 3 Steps to Sketch YouTube Is Sec X Continuous No, the function \(f(x) = \sec x\) is not continuous everywhere. No, the function f (x) = sec x is not continuous on the interval [− π 2, π 2] because the function is undefined at x = − π 2 and. It is not sensible to say a function is not continuous where it is not defined. When we. Is Sec X Continuous.