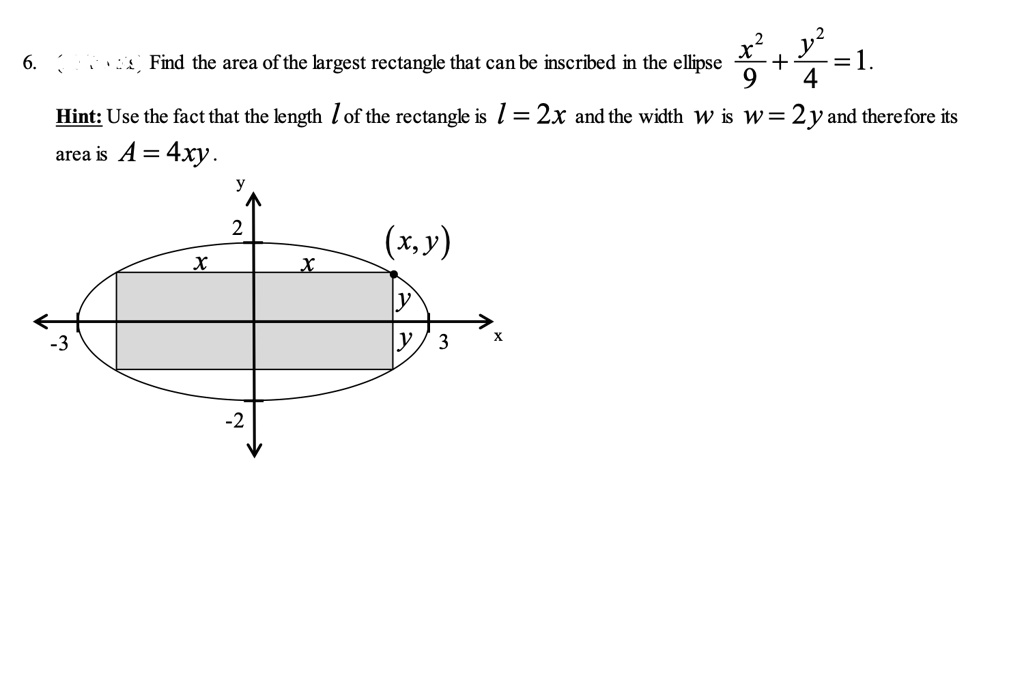
Largest Rectangle In An Ellipse . Area of largest rectangle = 2ab. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Find the area of the largest rectangle that can be inscribed in the ellipse with the equation (x 2)/4 + (y 2)/9 = 1. Explore math with our beautiful, free online graphing calculator. Learn how to find the maximum area of a rectangle that can be inscribed in an ellipse. Hence the largest rectangle fitting into an ellipse with a=2 and b=1 has the area a=4(sqrt(2)/sqrt(2)=4. The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is a circle of radius $a$ in $(\hat x,y)$ coordinates, where $\hat x=\dfrac{a}{b}x$. Where a is half of the major axis of the ellipse and b is half of the minor axis of the ellipse. Inscribe the largest possible rectangle inside this circle, which turns out to be a square of area $2a^2$.
from www.numerade.com
Where a is half of the major axis of the ellipse and b is half of the minor axis of the ellipse. Find the area of the largest rectangle that can be inscribed in the ellipse with the equation (x 2)/4 + (y 2)/9 = 1. Explore math with our beautiful, free online graphing calculator. Hence the largest rectangle fitting into an ellipse with a=2 and b=1 has the area a=4(sqrt(2)/sqrt(2)=4. Area of largest rectangle = 2ab. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Inscribe the largest possible rectangle inside this circle, which turns out to be a square of area $2a^2$. The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is a circle of radius $a$ in $(\hat x,y)$ coordinates, where $\hat x=\dfrac{a}{b}x$. Learn how to find the maximum area of a rectangle that can be inscribed in an ellipse.
SOLVED Find the area of the largest rectangle that can be inscribed in
Largest Rectangle In An Ellipse Explore math with our beautiful, free online graphing calculator. Area of largest rectangle = 2ab. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Inscribe the largest possible rectangle inside this circle, which turns out to be a square of area $2a^2$. Where a is half of the major axis of the ellipse and b is half of the minor axis of the ellipse. Hence the largest rectangle fitting into an ellipse with a=2 and b=1 has the area a=4(sqrt(2)/sqrt(2)=4. Learn how to find the maximum area of a rectangle that can be inscribed in an ellipse. Find the area of the largest rectangle that can be inscribed in the ellipse with the equation (x 2)/4 + (y 2)/9 = 1. The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is a circle of radius $a$ in $(\hat x,y)$ coordinates, where $\hat x=\dfrac{a}{b}x$. Explore math with our beautiful, free online graphing calculator.
From www.chegg.com
Solved Find the dimensions and the area of the largest Largest Rectangle In An Ellipse The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is a circle of radius $a$ in $(\hat x,y)$ coordinates, where $\hat x=\dfrac{a}{b}x$. Where a is half of the major axis of the ellipse and b is half of the minor axis of the ellipse. Learn how to find the maximum area of a rectangle that can be inscribed in an ellipse. Area. Largest Rectangle In An Ellipse.
From www.bartleby.com
Answered Find the dimensions of the largest… bartleby Largest Rectangle In An Ellipse Area of largest rectangle = 2ab. Find the area of the largest rectangle that can be inscribed in the ellipse with the equation (x 2)/4 + (y 2)/9 = 1. Explore math with our beautiful, free online graphing calculator. The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is a circle of radius $a$ in $(\hat x,y)$ coordinates, where $\hat x=\dfrac{a}{b}x$. Learn. Largest Rectangle In An Ellipse.
From www.numerade.com
SOLVED find the dimensions of the largest rectangle which can be Largest Rectangle In An Ellipse Find the area of the largest rectangle that can be inscribed in the ellipse with the equation (x 2)/4 + (y 2)/9 = 1. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is a circle of radius $a$ in $(\hat x,y)$ coordinates, where $\hat x=\dfrac{a}{b}x$. Learn how to. Largest Rectangle In An Ellipse.
From www.youtube.com
Find the area of the greatest rectangle that can be inscribed in an Largest Rectangle In An Ellipse Inscribe the largest possible rectangle inside this circle, which turns out to be a square of area $2a^2$. Learn how to find the maximum area of a rectangle that can be inscribed in an ellipse. Where a is half of the major axis of the ellipse and b is half of the minor axis of the ellipse. Area of largest. Largest Rectangle In An Ellipse.
From www.youtube.com
RECTANGLE METHOD OF ELLIPSE CONSTRUCTION YouTube Largest Rectangle In An Ellipse Inscribe the largest possible rectangle inside this circle, which turns out to be a square of area $2a^2$. Hence the largest rectangle fitting into an ellipse with a=2 and b=1 has the area a=4(sqrt(2)/sqrt(2)=4. Learn how to find the maximum area of a rectangle that can be inscribed in an ellipse. Graph functions, plot points, visualize algebraic equations, add sliders,. Largest Rectangle In An Ellipse.
From www.numerade.com
SOLVEDA rectangle is inscribed in an ellipse with major axis of length Largest Rectangle In An Ellipse The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is a circle of radius $a$ in $(\hat x,y)$ coordinates, where $\hat x=\dfrac{a}{b}x$. Where a is half of the major axis of the ellipse and b is half of the minor axis of the ellipse. Find the area of the largest rectangle that can be inscribed in the ellipse with the equation (x. Largest Rectangle In An Ellipse.
From www.youtube.com
Can You Find The Area of Greatest Rectangle in a Ellipse Maximum Area Largest Rectangle In An Ellipse Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Learn how to find the maximum area of a rectangle that can be inscribed in an ellipse. Explore math with our beautiful, free online graphing calculator. Where a is half of the major axis of the ellipse and b is half of the minor axis of the. Largest Rectangle In An Ellipse.
From www.youtube.com
Ellipse By Oblong Method(Rectangle Method) YouTube Largest Rectangle In An Ellipse Learn how to find the maximum area of a rectangle that can be inscribed in an ellipse. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Area of largest rectangle = 2ab. Hence the largest rectangle fitting into an ellipse with a=2 and b=1 has the area a=4(sqrt(2)/sqrt(2)=4. The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is. Largest Rectangle In An Ellipse.
From www.youtube.com
Find the area of largest rectangle that can be inscribed in an ellipse Largest Rectangle In An Ellipse Explore math with our beautiful, free online graphing calculator. Find the area of the largest rectangle that can be inscribed in the ellipse with the equation (x 2)/4 + (y 2)/9 = 1. Hence the largest rectangle fitting into an ellipse with a=2 and b=1 has the area a=4(sqrt(2)/sqrt(2)=4. Learn how to find the maximum area of a rectangle that. Largest Rectangle In An Ellipse.
From www.chegg.com
Solved Questions Find the area and the dimensions of the Largest Rectangle In An Ellipse Learn how to find the maximum area of a rectangle that can be inscribed in an ellipse. Where a is half of the major axis of the ellipse and b is half of the minor axis of the ellipse. Inscribe the largest possible rectangle inside this circle, which turns out to be a square of area $2a^2$. Explore math with. Largest Rectangle In An Ellipse.
From www.youtube.com
Draw an Ellipse Using The Rectangle Method (Oblong Method) YouTube Largest Rectangle In An Ellipse Hence the largest rectangle fitting into an ellipse with a=2 and b=1 has the area a=4(sqrt(2)/sqrt(2)=4. Explore math with our beautiful, free online graphing calculator. Area of largest rectangle = 2ab. Inscribe the largest possible rectangle inside this circle, which turns out to be a square of area $2a^2$. The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is a circle of. Largest Rectangle In An Ellipse.
From oneclass.com
OneClass Q1 . Find the area of the largest rectangle that can be Largest Rectangle In An Ellipse Area of largest rectangle = 2ab. Where a is half of the major axis of the ellipse and b is half of the minor axis of the ellipse. The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is a circle of radius $a$ in $(\hat x,y)$ coordinates, where $\hat x=\dfrac{a}{b}x$. Inscribe the largest possible rectangle inside this circle, which turns out to. Largest Rectangle In An Ellipse.
From www.youtube.com
ELLIPSE BY RECTANGLE METHOD IN Technical drawing Engineering Largest Rectangle In An Ellipse The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is a circle of radius $a$ in $(\hat x,y)$ coordinates, where $\hat x=\dfrac{a}{b}x$. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Area of largest rectangle = 2ab. Inscribe the largest possible rectangle inside this circle, which turns out to be a square of area $2a^2$. Hence the largest. Largest Rectangle In An Ellipse.
From www.softschools.com
Ellipse Standard Equation Largest Rectangle In An Ellipse Learn how to find the maximum area of a rectangle that can be inscribed in an ellipse. Explore math with our beautiful, free online graphing calculator. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Hence the largest rectangle fitting into an ellipse with a=2 and b=1 has the area a=4(sqrt(2)/sqrt(2)=4. Area of largest rectangle =. Largest Rectangle In An Ellipse.
From www.chegg.com
Solved Find the dimensions and the area of the largest Largest Rectangle In An Ellipse Area of largest rectangle = 2ab. Learn how to find the maximum area of a rectangle that can be inscribed in an ellipse. The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is a circle of radius $a$ in $(\hat x,y)$ coordinates, where $\hat x=\dfrac{a}{b}x$. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Hence the largest rectangle. Largest Rectangle In An Ellipse.
From www.houseofmath.com
What Is the Equation of an Ellipse? House of Math Largest Rectangle In An Ellipse Hence the largest rectangle fitting into an ellipse with a=2 and b=1 has the area a=4(sqrt(2)/sqrt(2)=4. Find the area of the largest rectangle that can be inscribed in the ellipse with the equation (x 2)/4 + (y 2)/9 = 1. Where a is half of the major axis of the ellipse and b is half of the minor axis of. Largest Rectangle In An Ellipse.
From www.chegg.com
Solved Use Lagrange multipliers to find the maximum area of Largest Rectangle In An Ellipse The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is a circle of radius $a$ in $(\hat x,y)$ coordinates, where $\hat x=\dfrac{a}{b}x$. Find the area of the largest rectangle that can be inscribed in the ellipse with the equation (x 2)/4 + (y 2)/9 = 1. Area of largest rectangle = 2ab. Hence the largest rectangle fitting into an ellipse with a=2. Largest Rectangle In An Ellipse.
From www.youtube.com
How to fit the biggest possible rectangle inside of an ellipse YouTube Largest Rectangle In An Ellipse Inscribe the largest possible rectangle inside this circle, which turns out to be a square of area $2a^2$. Explore math with our beautiful, free online graphing calculator. Where a is half of the major axis of the ellipse and b is half of the minor axis of the ellipse. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs,. Largest Rectangle In An Ellipse.
From www.numerade.com
SOLVED Sara Sirkel has drawn an ellipse with an inscribed rectangle Largest Rectangle In An Ellipse Learn how to find the maximum area of a rectangle that can be inscribed in an ellipse. Explore math with our beautiful, free online graphing calculator. Where a is half of the major axis of the ellipse and b is half of the minor axis of the ellipse. Inscribe the largest possible rectangle inside this circle, which turns out to. Largest Rectangle In An Ellipse.
From quizlet.com
Find the area of the largest rectangle that can be inscribed Quizlet Largest Rectangle In An Ellipse Inscribe the largest possible rectangle inside this circle, which turns out to be a square of area $2a^2$. Find the area of the largest rectangle that can be inscribed in the ellipse with the equation (x 2)/4 + (y 2)/9 = 1. The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is a circle of radius $a$ in $(\hat x,y)$ coordinates, where. Largest Rectangle In An Ellipse.
From brainly.in
Using integration, find the area of the largest rectangle that can be Largest Rectangle In An Ellipse Find the area of the largest rectangle that can be inscribed in the ellipse with the equation (x 2)/4 + (y 2)/9 = 1. Area of largest rectangle = 2ab. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Explore math with our beautiful, free online graphing calculator. Learn how to find the maximum area of. Largest Rectangle In An Ellipse.
From owlcation.com
How to Graph an Ellipse Given an Equation Owlcation Largest Rectangle In An Ellipse Inscribe the largest possible rectangle inside this circle, which turns out to be a square of area $2a^2$. Where a is half of the major axis of the ellipse and b is half of the minor axis of the ellipse. Area of largest rectangle = 2ab. Explore math with our beautiful, free online graphing calculator. Find the area of the. Largest Rectangle In An Ellipse.
From math.stackexchange.com
geometry Fitting a largest area ellipse into a rectangle Largest Rectangle In An Ellipse Hence the largest rectangle fitting into an ellipse with a=2 and b=1 has the area a=4(sqrt(2)/sqrt(2)=4. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Learn how to find the maximum area of a rectangle that can be inscribed in an ellipse. Find the area of the largest rectangle that can be inscribed in the ellipse. Largest Rectangle In An Ellipse.
From www.youtube.com
MCV4U Calculus Optimization Rectangle in Ellipse Example YouTube Largest Rectangle In An Ellipse Find the area of the largest rectangle that can be inscribed in the ellipse with the equation (x 2)/4 + (y 2)/9 = 1. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Hence the largest rectangle fitting into an ellipse with a=2 and b=1 has the area a=4(sqrt(2)/sqrt(2)=4. The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$. Largest Rectangle In An Ellipse.
From brainly.com
find the area of the largest rectangle that can be inscribed in the Largest Rectangle In An Ellipse Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Learn how to find the maximum area of a rectangle that can be inscribed in an ellipse. Where a is half of the major axis of the ellipse and b is half of the minor axis of the ellipse. Find the area of the largest rectangle that. Largest Rectangle In An Ellipse.
From www.toppr.com
( mathrm { OR } ) rind the area of greatest rectangle that can be Largest Rectangle In An Ellipse Inscribe the largest possible rectangle inside this circle, which turns out to be a square of area $2a^2$. The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is a circle of radius $a$ in $(\hat x,y)$ coordinates, where $\hat x=\dfrac{a}{b}x$. Find the area of the largest rectangle that can be inscribed in the ellipse with the equation (x 2)/4 + (y 2)/9. Largest Rectangle In An Ellipse.
From www.solutionspile.com
[Solved] 1)Drawing an ellipse with the rectangle method.2)D Largest Rectangle In An Ellipse Find the area of the largest rectangle that can be inscribed in the ellipse with the equation (x 2)/4 + (y 2)/9 = 1. The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is a circle of radius $a$ in $(\hat x,y)$ coordinates, where $\hat x=\dfrac{a}{b}x$. Area of largest rectangle = 2ab. Explore math with our beautiful, free online graphing calculator. Learn. Largest Rectangle In An Ellipse.
From www.geeksforgeeks.org
Find the area of the largest rectangle that can be inscribed in the Largest Rectangle In An Ellipse Where a is half of the major axis of the ellipse and b is half of the minor axis of the ellipse. Find the area of the largest rectangle that can be inscribed in the ellipse with the equation (x 2)/4 + (y 2)/9 = 1. Learn how to find the maximum area of a rectangle that can be inscribed. Largest Rectangle In An Ellipse.
From www.numerade.com
SOLVEDFind the area of the largest rectangle that can be inscribed in Largest Rectangle In An Ellipse Explore math with our beautiful, free online graphing calculator. Inscribe the largest possible rectangle inside this circle, which turns out to be a square of area $2a^2$. Learn how to find the maximum area of a rectangle that can be inscribed in an ellipse. Where a is half of the major axis of the ellipse and b is half of. Largest Rectangle In An Ellipse.
From www.numerade.com
SOLVEDRectangle of longest perimeter in an ellipse Find the dimensions Largest Rectangle In An Ellipse Area of largest rectangle = 2ab. Explore math with our beautiful, free online graphing calculator. The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is a circle of radius $a$ in $(\hat x,y)$ coordinates, where $\hat x=\dfrac{a}{b}x$. Hence the largest rectangle fitting into an ellipse with a=2 and b=1 has the area a=4(sqrt(2)/sqrt(2)=4. Inscribe the largest possible rectangle inside this circle, which. Largest Rectangle In An Ellipse.
From www.numerade.com
SOLVED Find the area of the largest rectangle that can be inscribed in Largest Rectangle In An Ellipse Hence the largest rectangle fitting into an ellipse with a=2 and b=1 has the area a=4(sqrt(2)/sqrt(2)=4. Inscribe the largest possible rectangle inside this circle, which turns out to be a square of area $2a^2$. The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ is a circle of radius $a$ in $(\hat x,y)$ coordinates, where $\hat x=\dfrac{a}{b}x$. Explore math with our beautiful, free. Largest Rectangle In An Ellipse.
From www.teachoo.com
Example 2 Find area enclosed by ellipse x2/a2 + y2/b2 = 1 Largest Rectangle In An Ellipse Learn how to find the maximum area of a rectangle that can be inscribed in an ellipse. Hence the largest rectangle fitting into an ellipse with a=2 and b=1 has the area a=4(sqrt(2)/sqrt(2)=4. Inscribe the largest possible rectangle inside this circle, which turns out to be a square of area $2a^2$. Find the area of the largest rectangle that can. Largest Rectangle In An Ellipse.
From www.youtube.com
Derivatives Optimization Rectangle Inscribed in Ellipse YouTube Largest Rectangle In An Ellipse Explore math with our beautiful, free online graphing calculator. Where a is half of the major axis of the ellipse and b is half of the minor axis of the ellipse. Find the area of the largest rectangle that can be inscribed in the ellipse with the equation (x 2)/4 + (y 2)/9 = 1. The ellipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2}. Largest Rectangle In An Ellipse.
From www.coursehero.com
[Solved] 2a) Find the largest rectangle that you can fit into the Largest Rectangle In An Ellipse Hence the largest rectangle fitting into an ellipse with a=2 and b=1 has the area a=4(sqrt(2)/sqrt(2)=4. Where a is half of the major axis of the ellipse and b is half of the minor axis of the ellipse. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Explore math with our beautiful, free online graphing calculator.. Largest Rectangle In An Ellipse.
From www.numerade.com
SOLVED Find the area of the largest rectangle that can be inscribed in Largest Rectangle In An Ellipse Explore math with our beautiful, free online graphing calculator. Hence the largest rectangle fitting into an ellipse with a=2 and b=1 has the area a=4(sqrt(2)/sqrt(2)=4. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. Area of largest rectangle = 2ab. Learn how to find the maximum area of a rectangle that can be inscribed in an. Largest Rectangle In An Ellipse.