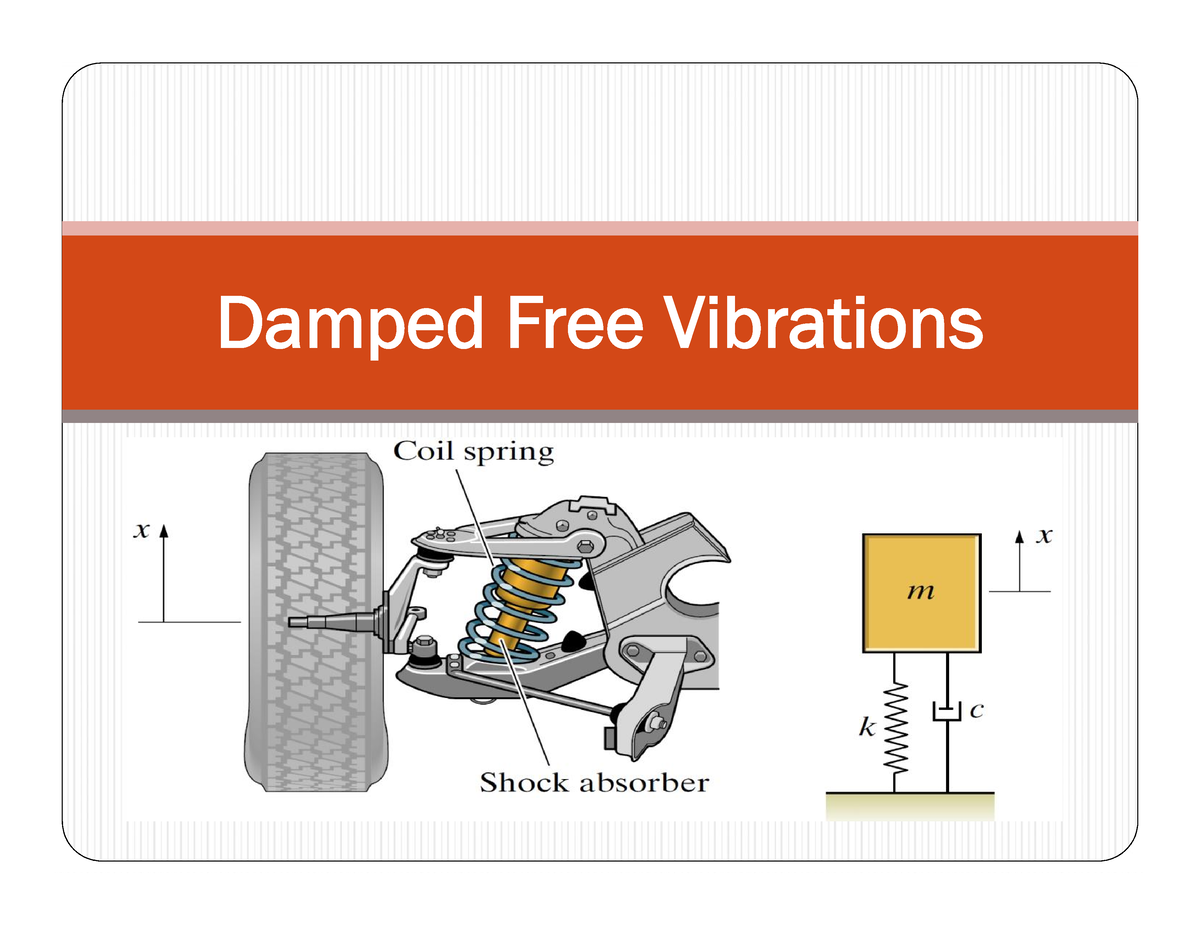
Differential Equation Of Damped Free Vibration . Setting up damp free vibration problems. Linearize a nonlinear equation of motion. You may have forgotten what a dashpot (or damper) does. Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). The solution to the system differential equation is of the form \[ x(t) = a e^{rt}, \] where \(a\) is constant and the value(s) of \(r\) can be can be obtained by. We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course. (ii) solve the differential equation. (i) get a differential equation for s using f=ma. Solving the eom for free damped vibrations. To solve this equation of motion we propose the following complex trial function: Using 2nd order homogeneous differential equations to solve. \[y_{a}(t)=\re a_{c} e^{\lambda t} \tag{13.31} \label{13.31}\]
from www.studocu.com
Using 2nd order homogeneous differential equations to solve. Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course. Linearize a nonlinear equation of motion. To solve this equation of motion we propose the following complex trial function: (i) get a differential equation for s using f=ma. You may have forgotten what a dashpot (or damper) does. Solving the eom for free damped vibrations. \[y_{a}(t)=\re a_{c} e^{\lambda t} \tag{13.31} \label{13.31}\] (ii) solve the differential equation.
L2 Damped Vibration summary notes Damped Free Vibrations Damping
Differential Equation Of Damped Free Vibration \[y_{a}(t)=\re a_{c} e^{\lambda t} \tag{13.31} \label{13.31}\] Using 2nd order homogeneous differential equations to solve. \[y_{a}(t)=\re a_{c} e^{\lambda t} \tag{13.31} \label{13.31}\] Solving the eom for free damped vibrations. To solve this equation of motion we propose the following complex trial function: Linearize a nonlinear equation of motion. Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). (ii) solve the differential equation. You may have forgotten what a dashpot (or damper) does. The solution to the system differential equation is of the form \[ x(t) = a e^{rt}, \] where \(a\) is constant and the value(s) of \(r\) can be can be obtained by. Setting up damp free vibration problems. (i) get a differential equation for s using f=ma. We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course.
From giotkkoxw.blob.core.windows.net
Damped Free Vibration Derivation at Hans Rhodes blog Differential Equation Of Damped Free Vibration The solution to the system differential equation is of the form \[ x(t) = a e^{rt}, \] where \(a\) is constant and the value(s) of \(r\) can be can be obtained by. \[y_{a}(t)=\re a_{c} e^{\lambda t} \tag{13.31} \label{13.31}\] To solve this equation of motion we propose the following complex trial function: Solving the eom for free damped vibrations. Linearize a. Differential Equation Of Damped Free Vibration.
From www.youtube.com
M308 Differential Equations Damped Free Vibration (Over damped Motion Differential Equation Of Damped Free Vibration \[y_{a}(t)=\re a_{c} e^{\lambda t} \tag{13.31} \label{13.31}\] Solving the eom for free damped vibrations. We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course. (ii) solve the differential equation. Linearize a nonlinear equation of motion. (i) get a differential equation for s using f=ma. Setting up damp. Differential Equation Of Damped Free Vibration.
From www.youtube.com
Differential Equations Free Damped Vibration Example with Laplace Differential Equation Of Damped Free Vibration The solution to the system differential equation is of the form \[ x(t) = a e^{rt}, \] where \(a\) is constant and the value(s) of \(r\) can be can be obtained by. Linearize a nonlinear equation of motion. (i) get a differential equation for s using f=ma. \[y_{a}(t)=\re a_{c} e^{\lambda t} \tag{13.31} \label{13.31}\] Free damped vibration in free, damped vibration,. Differential Equation Of Damped Free Vibration.
From www.slideserve.com
PPT Chapter 5 Modeling with HigherOrder Differential Equations Differential Equation Of Damped Free Vibration Using 2nd order homogeneous differential equations to solve. Linearize a nonlinear equation of motion. (i) get a differential equation for s using f=ma. Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). To solve this equation of motion we propose the following complex trial function: You may have forgotten what a dashpot (or damper). Differential Equation Of Damped Free Vibration.
From www.youtube.com
Forced Vibrations, Critical Damping and the Effects of Resonance YouTube Differential Equation Of Damped Free Vibration (ii) solve the differential equation. We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course. To solve this equation of motion we propose the following complex trial function: \[y_{a}(t)=\re a_{c} e^{\lambda t} \tag{13.31} \label{13.31}\] The solution to the system differential equation is of the form \[. Differential Equation Of Damped Free Vibration.
From www.slideserve.com
PPT Mechanical Vibrations PowerPoint Presentation, free download ID Differential Equation Of Damped Free Vibration The solution to the system differential equation is of the form \[ x(t) = a e^{rt}, \] where \(a\) is constant and the value(s) of \(r\) can be can be obtained by. (ii) solve the differential equation. Using 2nd order homogeneous differential equations to solve. We are still going to assume that there will be no external forces acting on. Differential Equation Of Damped Free Vibration.
From www.numerade.com
SOLVED Damped free vibrations can be X modeled by a block of mass m Differential Equation Of Damped Free Vibration Using 2nd order homogeneous differential equations to solve. To solve this equation of motion we propose the following complex trial function: Linearize a nonlinear equation of motion. We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course. (ii) solve the differential equation. Solving the eom for. Differential Equation Of Damped Free Vibration.
From www.chegg.com
Solved Damped free vibrations can be modeled by a block of Differential Equation Of Damped Free Vibration Setting up damp free vibration problems. We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course. To solve this equation of motion we propose the following complex trial function: Linearize a nonlinear equation of motion. You may have forgotten what a dashpot (or damper) does. Free. Differential Equation Of Damped Free Vibration.
From www.youtube.com
M308 Differential Equations, Section 3.7(5/8) Damped Free Vibrations Differential Equation Of Damped Free Vibration Using 2nd order homogeneous differential equations to solve. Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). The solution to the system differential equation is of the form \[ x(t) = a e^{rt}, \] where \(a\) is constant and the value(s) of \(r\) can be can be obtained by. (i) get a differential equation. Differential Equation Of Damped Free Vibration.
From www.researchgate.net
Free vibration of systems with four levels of damping (a) = 5, (b Differential Equation Of Damped Free Vibration The solution to the system differential equation is of the form \[ x(t) = a e^{rt}, \] where \(a\) is constant and the value(s) of \(r\) can be can be obtained by. We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course. (i) get a differential. Differential Equation Of Damped Free Vibration.
From www.youtube.com
Free Vibrations and the Effects of Damping with Different Damping Differential Equation Of Damped Free Vibration Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). To solve this equation of motion we propose the following complex trial function: Setting up damp free vibration problems. Linearize a nonlinear equation of motion. You may have forgotten what a dashpot (or damper) does. (ii) solve the differential equation. (i) get a differential equation. Differential Equation Of Damped Free Vibration.
From www.youtube.com
Vibration Lec 6 Free Damped Vibration Part 3 (Under_Damping) Mech Differential Equation Of Damped Free Vibration (i) get a differential equation for s using f=ma. Setting up damp free vibration problems. We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course. Solving the eom for free damped vibrations. Using 2nd order homogeneous differential equations to solve. (ii) solve the differential equation. Free. Differential Equation Of Damped Free Vibration.
From www.studypool.com
SOLUTION Lec 6 chapter 3 free damped vibrations modified Studypool Differential Equation Of Damped Free Vibration Solving the eom for free damped vibrations. Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). \[y_{a}(t)=\re a_{c} e^{\lambda t} \tag{13.31} \label{13.31}\] (ii) solve the differential equation. (i) get a differential equation for s using f=ma. The solution to the system differential equation is of the form \[ x(t) = a e^{rt}, \] where. Differential Equation Of Damped Free Vibration.
From www.youtube.com
M308 Differential Equations Damped Free Vibration Ex4 YouTube Differential Equation Of Damped Free Vibration You may have forgotten what a dashpot (or damper) does. Setting up damp free vibration problems. Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). The solution to the system differential equation is of the form \[ x(t) = a e^{rt}, \] where \(a\) is constant and the value(s) of \(r\) can be can. Differential Equation Of Damped Free Vibration.
From giotkkoxw.blob.core.windows.net
Damped Free Vibration Derivation at Hans Rhodes blog Differential Equation Of Damped Free Vibration We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course. Linearize a nonlinear equation of motion. (ii) solve the differential equation. You may have forgotten what a dashpot (or damper) does. Using 2nd order homogeneous differential equations to solve. The solution to the system differential equation. Differential Equation Of Damped Free Vibration.
From mechanicsmap.psu.edu
Mechanics Map Viscous Damped Free Vibrations Differential Equation Of Damped Free Vibration Solving the eom for free damped vibrations. Linearize a nonlinear equation of motion. The solution to the system differential equation is of the form \[ x(t) = a e^{rt}, \] where \(a\) is constant and the value(s) of \(r\) can be can be obtained by. You may have forgotten what a dashpot (or damper) does. \[y_{a}(t)=\re a_{c} e^{\lambda t} \tag{13.31}. Differential Equation Of Damped Free Vibration.
From giotkkoxw.blob.core.windows.net
Damped Free Vibration Derivation at Hans Rhodes blog Differential Equation Of Damped Free Vibration Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). Solving the eom for free damped vibrations. \[y_{a}(t)=\re a_{c} e^{\lambda t} \tag{13.31} \label{13.31}\] Linearize a nonlinear equation of motion. We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course. (i) get. Differential Equation Of Damped Free Vibration.
From www.youtube.com
Free vibration with viscous damping Mechanical Engineering Lecture Differential Equation Of Damped Free Vibration Linearize a nonlinear equation of motion. You may have forgotten what a dashpot (or damper) does. Solving the eom for free damped vibrations. Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). \[y_{a}(t)=\re a_{c} e^{\lambda t} \tag{13.31} \label{13.31}\] To solve this equation of motion we propose the following complex trial function: We are still. Differential Equation Of Damped Free Vibration.
From www.studocu.com
L2 Damped Vibration summary notes Damped Free Vibrations Damping Differential Equation Of Damped Free Vibration Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). The solution to the system differential equation is of the form \[ x(t) = a e^{rt}, \] where \(a\) is constant and the value(s) of \(r\) can be can be obtained by. You may have forgotten what a dashpot (or damper) does. (i) get a. Differential Equation Of Damped Free Vibration.
From www.chegg.com
Solved Free damped vibrations. The damping is provided by Differential Equation Of Damped Free Vibration To solve this equation of motion we propose the following complex trial function: (ii) solve the differential equation. You may have forgotten what a dashpot (or damper) does. The solution to the system differential equation is of the form \[ x(t) = a e^{rt}, \] where \(a\) is constant and the value(s) of \(r\) can be can be obtained by.. Differential Equation Of Damped Free Vibration.
From www.coursehero.com
[Solved] Damped Free Vibration of Single Degree of Freedom System 1 Differential Equation Of Damped Free Vibration You may have forgotten what a dashpot (or damper) does. Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). To solve this equation of motion we propose the following complex trial function: The solution to the system differential equation is of the form \[ x(t) = a e^{rt}, \] where \(a\) is constant and. Differential Equation Of Damped Free Vibration.
From www.youtube.com
M308 Differential Equations Damped Free Vibrations (Under damped Differential Equation Of Damped Free Vibration We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course. You may have forgotten what a dashpot (or damper) does. Solving the eom for free damped vibrations. Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). Using 2nd order homogeneous. Differential Equation Of Damped Free Vibration.
From www.youtube.com
M308 Differential Equations Damped Free Vibration Ex3 YouTube Differential Equation Of Damped Free Vibration Solving the eom for free damped vibrations. Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). \[y_{a}(t)=\re a_{c} e^{\lambda t} \tag{13.31} \label{13.31}\] To solve this equation of motion we propose the following complex trial function: (ii) solve the differential equation. (i) get a differential equation for s using f=ma. You may have forgotten what. Differential Equation Of Damped Free Vibration.
From www.youtube.com
FREE DAMPED VIBRATION [Solution of Differential Equation] GATE Differential Equation Of Damped Free Vibration Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). Solving the eom for free damped vibrations. The solution to the system differential equation is of the form \[ x(t) = a e^{rt}, \] where \(a\) is constant and the value(s) of \(r\) can be can be obtained by. You may have forgotten what a. Differential Equation Of Damped Free Vibration.
From www.slideserve.com
PPT Damped Oscillations PowerPoint Presentation, free download ID Differential Equation Of Damped Free Vibration Linearize a nonlinear equation of motion. (ii) solve the differential equation. We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course. (i) get a differential equation for s using f=ma. Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). Using. Differential Equation Of Damped Free Vibration.
From www.youtube.com
Damped Free Vibration PART I (SPRING MASS DAMPER SYSTEM GOVERNING Differential Equation Of Damped Free Vibration To solve this equation of motion we propose the following complex trial function: Using 2nd order homogeneous differential equations to solve. You may have forgotten what a dashpot (or damper) does. We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course. (ii) solve the differential equation.. Differential Equation Of Damped Free Vibration.
From dxohdptkx.blob.core.windows.net
Vibration Equations at Scheetz blog Differential Equation Of Damped Free Vibration (ii) solve the differential equation. We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course. (i) get a differential equation for s using f=ma. Setting up damp free vibration problems. The solution to the system differential equation is of the form \[ x(t) = a e^{rt},. Differential Equation Of Damped Free Vibration.
From mechanicsmap.psu.edu
Mechanics Map Friction Damped Free Vibration Differential Equation Of Damped Free Vibration Solving the eom for free damped vibrations. We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course. To solve this equation of motion we propose the following complex trial function: Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). Linearize. Differential Equation Of Damped Free Vibration.
From www.youtube.com
Ex Model Free Damped Vibration and Find Displacement Function YouTube Differential Equation Of Damped Free Vibration Solving the eom for free damped vibrations. (i) get a differential equation for s using f=ma. Linearize a nonlinear equation of motion. Using 2nd order homogeneous differential equations to solve. (ii) solve the differential equation. Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). To solve this equation of motion we propose the following. Differential Equation Of Damped Free Vibration.
From www.slideserve.com
PPT Lecture 2 Free Vibration of Single Degree of Freedom Systems Differential Equation Of Damped Free Vibration Solving the eom for free damped vibrations. Using 2nd order homogeneous differential equations to solve. Setting up damp free vibration problems. To solve this equation of motion we propose the following complex trial function: Linearize a nonlinear equation of motion. We are still going to assume that there will be no external forces acting on the system, with the exception. Differential Equation Of Damped Free Vibration.
From www.slideserve.com
PPT SECONDORDER DIFFERENTIAL EQUATIONS PowerPoint Presentation, free Differential Equation Of Damped Free Vibration Setting up damp free vibration problems. (ii) solve the differential equation. Solving the eom for free damped vibrations. Using 2nd order homogeneous differential equations to solve. The solution to the system differential equation is of the form \[ x(t) = a e^{rt}, \] where \(a\) is constant and the value(s) of \(r\) can be can be obtained by. Free damped. Differential Equation Of Damped Free Vibration.
From www.youtube.com
Undamped Free Vibration (Simple Harmonic Motion) Differential Differential Equation Of Damped Free Vibration (ii) solve the differential equation. You may have forgotten what a dashpot (or damper) does. Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course. (i) get a differential equation for. Differential Equation Of Damped Free Vibration.
From www.youtube.com
Free Mechanical Vibrations (Differential Equations) YouTube Differential Equation Of Damped Free Vibration Linearize a nonlinear equation of motion. To solve this equation of motion we propose the following complex trial function: (i) get a differential equation for s using f=ma. Solving the eom for free damped vibrations. We are still going to assume that there will be no external forces acting on the system, with the exception of damping of course. You. Differential Equation Of Damped Free Vibration.
From giotkkoxw.blob.core.windows.net
Damped Free Vibration Derivation at Hans Rhodes blog Differential Equation Of Damped Free Vibration (i) get a differential equation for s using f=ma. You may have forgotten what a dashpot (or damper) does. Setting up damp free vibration problems. Linearize a nonlinear equation of motion. Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). Using 2nd order homogeneous differential equations to solve. We are still going to assume. Differential Equation Of Damped Free Vibration.
From exyehdoxe.blob.core.windows.net
Vibration Damping Equation at Marvin Howard blog Differential Equation Of Damped Free Vibration \[y_{a}(t)=\re a_{c} e^{\lambda t} \tag{13.31} \label{13.31}\] (i) get a differential equation for s using f=ma. Linearize a nonlinear equation of motion. You may have forgotten what a dashpot (or damper) does. Using 2nd order homogeneous differential equations to solve. Free damped vibration in free, damped vibration, there is no external force ( [asciimath]f(t)=0[/asciimath] ). Setting up damp free vibration problems.. Differential Equation Of Damped Free Vibration.