Is Counting A Measurement . The counting measure $c : Can somebody tell me why the counting measure (so, if $s=p(x)$, then $\mu(a)$=infinity if $a$ isn't finite and $\mu(a)=$#$a$ if $a$ is finite). To count means to determine the cardinality of some finite set. The function # on p(s) is called counting measure. \mathcal p(x) \to [0, \infty]$ on $\mathcal p(x)$ is defined for all $e \in \mathcal p(x)$ by $c(e) = |e|$, and the triple. A measure on ($x,s$) is a function $\mu: For a ⊆ s, the cardinality of a is the number of elements in a, and is denoted #(a). Counting is the process of determining the number of elements of a finite set of objects; That is, determining the size of a set. Suppose that s is a finite set. If a ⊆ s then the cardinality of a is the number of. $\mu (\emptyset) = 0$$\mu (\bigcup \limits_ {k =1}^. Technically, since the natural numbers are usually defined as.
from imagexinnovation.com
The counting measure $c : Counting is the process of determining the number of elements of a finite set of objects; If a ⊆ s then the cardinality of a is the number of. Technically, since the natural numbers are usually defined as. Suppose that s is a finite set. To count means to determine the cardinality of some finite set. Can somebody tell me why the counting measure (so, if $s=p(x)$, then $\mu(a)$=infinity if $a$ isn't finite and $\mu(a)=$#$a$ if $a$ is finite). The function # on p(s) is called counting measure. For a ⊆ s, the cardinality of a is the number of elements in a, and is denoted #(a). $\mu (\emptyset) = 0$$\mu (\bigcup \limits_ {k =1}^.
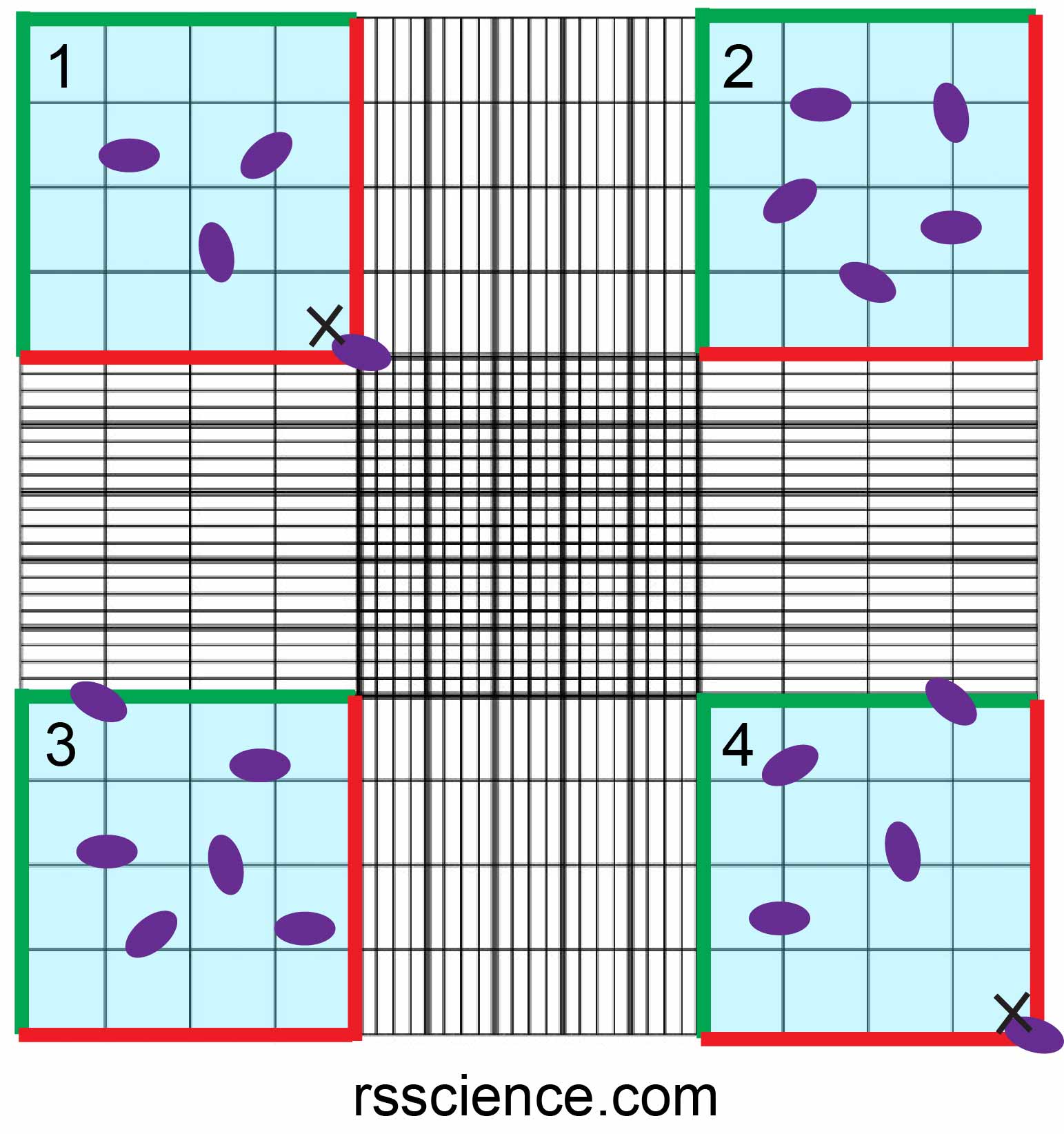
Jak używać Hemocytometru do liczenia komórekRS ' Science Image
Is Counting A Measurement Suppose that s is a finite set. Can somebody tell me why the counting measure (so, if $s=p(x)$, then $\mu(a)$=infinity if $a$ isn't finite and $\mu(a)=$#$a$ if $a$ is finite). The counting measure $c : $\mu (\emptyset) = 0$$\mu (\bigcup \limits_ {k =1}^. Technically, since the natural numbers are usually defined as. If a ⊆ s then the cardinality of a is the number of. The function # on p(s) is called counting measure. A measure on ($x,s$) is a function $\mu: Counting is the process of determining the number of elements of a finite set of objects; \mathcal p(x) \to [0, \infty]$ on $\mathcal p(x)$ is defined for all $e \in \mathcal p(x)$ by $c(e) = |e|$, and the triple. Suppose that s is a finite set. That is, determining the size of a set. To count means to determine the cardinality of some finite set. For a ⊆ s, the cardinality of a is the number of elements in a, and is denoted #(a).
From www.youtube.com
Accuracy Of Measuring Instruments Least Count of Measuring Is Counting A Measurement $\mu (\emptyset) = 0$$\mu (\bigcup \limits_ {k =1}^. Technically, since the natural numbers are usually defined as. For a ⊆ s, the cardinality of a is the number of elements in a, and is denoted #(a). \mathcal p(x) \to [0, \infty]$ on $\mathcal p(x)$ is defined for all $e \in \mathcal p(x)$ by $c(e) = |e|$, and the triple. The. Is Counting A Measurement.
From www.worksheeto.com
16 Best Images of Kindergarten Worksheets Measuring Inches Measuring Is Counting A Measurement Can somebody tell me why the counting measure (so, if $s=p(x)$, then $\mu(a)$=infinity if $a$ isn't finite and $\mu(a)=$#$a$ if $a$ is finite). Suppose that s is a finite set. Technically, since the natural numbers are usually defined as. To count means to determine the cardinality of some finite set. If a ⊆ s then the cardinality of a is. Is Counting A Measurement.
From pxhere.com
Free Images distance, measure, ruler, label, protractor, mathematics Is Counting A Measurement The function # on p(s) is called counting measure. A measure on ($x,s$) is a function $\mu: Suppose that s is a finite set. For a ⊆ s, the cardinality of a is the number of elements in a, and is denoted #(a). $\mu (\emptyset) = 0$$\mu (\bigcup \limits_ {k =1}^. That is, determining the size of a set. Can. Is Counting A Measurement.
From www.walmart.com
33 Liter / 50 lbs Rice Container with Measuring Cup BPA free For Rice Is Counting A Measurement Suppose that s is a finite set. For a ⊆ s, the cardinality of a is the number of elements in a, and is denoted #(a). The function # on p(s) is called counting measure. Technically, since the natural numbers are usually defined as. A measure on ($x,s$) is a function $\mu: \mathcal p(x) \to [0, \infty]$ on $\mathcal p(x)$. Is Counting A Measurement.
From imagexinnovation.com
Jak używać Hemocytometru do liczenia komórekRS ' Science Image Is Counting A Measurement The counting measure $c : Counting is the process of determining the number of elements of a finite set of objects; That is, determining the size of a set. Suppose that s is a finite set. To count means to determine the cardinality of some finite set. Technically, since the natural numbers are usually defined as. Can somebody tell me. Is Counting A Measurement.
From www.doubtnut.com
Find the least count of the measuring cylinder used and the volume of Is Counting A Measurement The function # on p(s) is called counting measure. If a ⊆ s then the cardinality of a is the number of. To count means to determine the cardinality of some finite set. The counting measure $c : That is, determining the size of a set. Can somebody tell me why the counting measure (so, if $s=p(x)$, then $\mu(a)$=infinity if. Is Counting A Measurement.
From www.worksheeto.com
13 Best Images of 1st Grade Cut And Paste Math Worksheets Balance Is Counting A Measurement To count means to determine the cardinality of some finite set. $\mu (\emptyset) = 0$$\mu (\bigcup \limits_ {k =1}^. The counting measure $c : For a ⊆ s, the cardinality of a is the number of elements in a, and is denoted #(a). A measure on ($x,s$) is a function $\mu: Counting is the process of determining the number of. Is Counting A Measurement.
From materialmediagambrel.z14.web.core.windows.net
Measurement For Third Grade Is Counting A Measurement The function # on p(s) is called counting measure. $\mu (\emptyset) = 0$$\mu (\bigcup \limits_ {k =1}^. Suppose that s is a finite set. Counting is the process of determining the number of elements of a finite set of objects; \mathcal p(x) \to [0, \infty]$ on $\mathcal p(x)$ is defined for all $e \in \mathcal p(x)$ by $c(e) = |e|$,. Is Counting A Measurement.
From www.pinterest.com
Measuring Length Worksheet Have Fun Teaching Measurement worksheets Is Counting A Measurement The function # on p(s) is called counting measure. $\mu (\emptyset) = 0$$\mu (\bigcup \limits_ {k =1}^. That is, determining the size of a set. To count means to determine the cardinality of some finite set. Counting is the process of determining the number of elements of a finite set of objects; Suppose that s is a finite set. The. Is Counting A Measurement.
From kidskonnect.com
Measurement and Data Measuring Area by Counting Unit Squares CCSS 3.MD Is Counting A Measurement If a ⊆ s then the cardinality of a is the number of. Counting is the process of determining the number of elements of a finite set of objects; \mathcal p(x) \to [0, \infty]$ on $\mathcal p(x)$ is defined for all $e \in \mathcal p(x)$ by $c(e) = |e|$, and the triple. Can somebody tell me why the counting measure. Is Counting A Measurement.
From www.pinterest.com
Pin on All Things Math for K2 Is Counting A Measurement To count means to determine the cardinality of some finite set. Technically, since the natural numbers are usually defined as. \mathcal p(x) \to [0, \infty]$ on $\mathcal p(x)$ is defined for all $e \in \mathcal p(x)$ by $c(e) = |e|$, and the triple. A measure on ($x,s$) is a function $\mu: For a ⊆ s, the cardinality of a is. Is Counting A Measurement.
From templates.udlvirtual.edu.pe
Free Measurement Printables Printable Templates Is Counting A Measurement Technically, since the natural numbers are usually defined as. $\mu (\emptyset) = 0$$\mu (\bigcup \limits_ {k =1}^. Can somebody tell me why the counting measure (so, if $s=p(x)$, then $\mu(a)$=infinity if $a$ isn't finite and $\mu(a)=$#$a$ if $a$ is finite). Suppose that s is a finite set. Counting is the process of determining the number of elements of a finite. Is Counting A Measurement.
From shop.luckylittlelearners.com
Lucky to Learn Math Unit 7 Measurement Anchor Chart Measuring Is Counting A Measurement A measure on ($x,s$) is a function $\mu: Suppose that s is a finite set. $\mu (\emptyset) = 0$$\mu (\bigcup \limits_ {k =1}^. The function # on p(s) is called counting measure. For a ⊆ s, the cardinality of a is the number of elements in a, and is denoted #(a). Technically, since the natural numbers are usually defined as.. Is Counting A Measurement.
From www.findel-international.com
E8L32414 Academy Glass Measuring Cylinder 25ml Pack of 10 Findel Is Counting A Measurement Can somebody tell me why the counting measure (so, if $s=p(x)$, then $\mu(a)$=infinity if $a$ isn't finite and $\mu(a)=$#$a$ if $a$ is finite). Suppose that s is a finite set. The function # on p(s) is called counting measure. Counting is the process of determining the number of elements of a finite set of objects; Technically, since the natural numbers. Is Counting A Measurement.
From www.facebook.com
Frequency counter Measuring Tools & Sensors Oklahoma City, Oklahoma Is Counting A Measurement To count means to determine the cardinality of some finite set. \mathcal p(x) \to [0, \infty]$ on $\mathcal p(x)$ is defined for all $e \in \mathcal p(x)$ by $c(e) = |e|$, and the triple. If a ⊆ s then the cardinality of a is the number of. $\mu (\emptyset) = 0$$\mu (\bigcup \limits_ {k =1}^. A measure on ($x,s$) is. Is Counting A Measurement.
From www.walmart.com
33 Liter / 50 lbs Rice Container with Measuring Cup BPA free For Rice Is Counting A Measurement If a ⊆ s then the cardinality of a is the number of. A measure on ($x,s$) is a function $\mu: $\mu (\emptyset) = 0$$\mu (\bigcup \limits_ {k =1}^. \mathcal p(x) \to [0, \infty]$ on $\mathcal p(x)$ is defined for all $e \in \mathcal p(x)$ by $c(e) = |e|$, and the triple. The function # on p(s) is called counting. Is Counting A Measurement.
From www.walmart.com
CENL Walker metering with a clip and lane rope, used to measure steps Is Counting A Measurement To count means to determine the cardinality of some finite set. For a ⊆ s, the cardinality of a is the number of elements in a, and is denoted #(a). Can somebody tell me why the counting measure (so, if $s=p(x)$, then $\mu(a)$=infinity if $a$ isn't finite and $\mu(a)=$#$a$ if $a$ is finite). The function # on p(s) is called. Is Counting A Measurement.
From www.unmisravle.com
Non Standard Measurement Worksheets Grade 1 Is Counting A Measurement To count means to determine the cardinality of some finite set. The counting measure $c : That is, determining the size of a set. Suppose that s is a finite set. Counting is the process of determining the number of elements of a finite set of objects; \mathcal p(x) \to [0, \infty]$ on $\mathcal p(x)$ is defined for all $e. Is Counting A Measurement.
From www.indiamart.com
Piece Counting Scales, For Weighing, Weighing Capacity 100 Kg, Rs 7000 Is Counting A Measurement The counting measure $c : \mathcal p(x) \to [0, \infty]$ on $\mathcal p(x)$ is defined for all $e \in \mathcal p(x)$ by $c(e) = |e|$, and the triple. Suppose that s is a finite set. Counting is the process of determining the number of elements of a finite set of objects; Technically, since the natural numbers are usually defined as.. Is Counting A Measurement.
From showgilit.weebly.com
showgilit Blog Is Counting A Measurement Counting is the process of determining the number of elements of a finite set of objects; Suppose that s is a finite set. For a ⊆ s, the cardinality of a is the number of elements in a, and is denoted #(a). The counting measure $c : \mathcal p(x) \to [0, \infty]$ on $\mathcal p(x)$ is defined for all $e. Is Counting A Measurement.
From mavink.com
Unit Measurement Chart Is Counting A Measurement If a ⊆ s then the cardinality of a is the number of. For a ⊆ s, the cardinality of a is the number of elements in a, and is denoted #(a). Can somebody tell me why the counting measure (so, if $s=p(x)$, then $\mu(a)$=infinity if $a$ isn't finite and $\mu(a)=$#$a$ if $a$ is finite). Suppose that s is a. Is Counting A Measurement.
From exyglkhri.blob.core.windows.net
What Height Bar Stools For 42 Inch Counter at Sarah Curry blog Is Counting A Measurement If a ⊆ s then the cardinality of a is the number of. The counting measure $c : That is, determining the size of a set. For a ⊆ s, the cardinality of a is the number of elements in a, and is denoted #(a). To count means to determine the cardinality of some finite set. \mathcal p(x) \to [0,. Is Counting A Measurement.
From www.calameo.com
Calaméo Lets Play Counting And Measuring Preschool 3 2021 Is Counting A Measurement Technically, since the natural numbers are usually defined as. To count means to determine the cardinality of some finite set. Can somebody tell me why the counting measure (so, if $s=p(x)$, then $\mu(a)$=infinity if $a$ isn't finite and $\mu(a)=$#$a$ if $a$ is finite). Suppose that s is a finite set. A measure on ($x,s$) is a function $\mu: \mathcal p(x). Is Counting A Measurement.
From printableruleractualsize.com
Printable Counting Ruler Printable Ruler Actual Size Is Counting A Measurement Can somebody tell me why the counting measure (so, if $s=p(x)$, then $\mu(a)$=infinity if $a$ isn't finite and $\mu(a)=$#$a$ if $a$ is finite). If a ⊆ s then the cardinality of a is the number of. That is, determining the size of a set. Technically, since the natural numbers are usually defined as. A measure on ($x,s$) is a function. Is Counting A Measurement.
From learningcampusgland.z21.web.core.windows.net
Non Standard Units Of Measurement Worksheets Is Counting A Measurement If a ⊆ s then the cardinality of a is the number of. $\mu (\emptyset) = 0$$\mu (\bigcup \limits_ {k =1}^. To count means to determine the cardinality of some finite set. Can somebody tell me why the counting measure (so, if $s=p(x)$, then $\mu(a)$=infinity if $a$ isn't finite and $\mu(a)=$#$a$ if $a$ is finite). \mathcal p(x) \to [0, \infty]$. Is Counting A Measurement.
From gaugehow.com
Least count of measuring instruments GaugeHow Mechanical Engineering Is Counting A Measurement Counting is the process of determining the number of elements of a finite set of objects; Technically, since the natural numbers are usually defined as. To count means to determine the cardinality of some finite set. For a ⊆ s, the cardinality of a is the number of elements in a, and is denoted #(a). The counting measure $c :. Is Counting A Measurement.
From pngtree.com
Counting Days Counting Measurement Future Photo Background And Picture Is Counting A Measurement A measure on ($x,s$) is a function $\mu: $\mu (\emptyset) = 0$$\mu (\bigcup \limits_ {k =1}^. Suppose that s is a finite set. That is, determining the size of a set. If a ⊆ s then the cardinality of a is the number of. Can somebody tell me why the counting measure (so, if $s=p(x)$, then $\mu(a)$=infinity if $a$ isn't. Is Counting A Measurement.
From www.2nd-grade-math-salamanders.com
Measurement Math Worksheets Measuring Length Is Counting A Measurement If a ⊆ s then the cardinality of a is the number of. For a ⊆ s, the cardinality of a is the number of elements in a, and is denoted #(a). The function # on p(s) is called counting measure. Technically, since the natural numbers are usually defined as. Suppose that s is a finite set. Can somebody tell. Is Counting A Measurement.
From worksheetcampuscodes.z21.web.core.windows.net
Second Grade Measurement Worksheets Is Counting A Measurement The counting measure $c : Technically, since the natural numbers are usually defined as. That is, determining the size of a set. A measure on ($x,s$) is a function $\mu: The function # on p(s) is called counting measure. Suppose that s is a finite set. Can somebody tell me why the counting measure (so, if $s=p(x)$, then $\mu(a)$=infinity if. Is Counting A Measurement.
From cleverlearner.com
Free printable worksheets on measuring sizes, tall and short. Is Counting A Measurement The function # on p(s) is called counting measure. The counting measure $c : If a ⊆ s then the cardinality of a is the number of. $\mu (\emptyset) = 0$$\mu (\bigcup \limits_ {k =1}^. Can somebody tell me why the counting measure (so, if $s=p(x)$, then $\mu(a)$=infinity if $a$ isn't finite and $\mu(a)=$#$a$ if $a$ is finite). That is,. Is Counting A Measurement.
From kidskonnect.com
Measurement and Data Measuring Area by Counting in Different Units Is Counting A Measurement For a ⊆ s, the cardinality of a is the number of elements in a, and is denoted #(a). The function # on p(s) is called counting measure. Technically, since the natural numbers are usually defined as. Can somebody tell me why the counting measure (so, if $s=p(x)$, then $\mu(a)$=infinity if $a$ isn't finite and $\mu(a)=$#$a$ if $a$ is finite).. Is Counting A Measurement.
From www.mathsdiary.com
MeasurementLong and Short Math Worksheets Is Counting A Measurement For a ⊆ s, the cardinality of a is the number of elements in a, and is denoted #(a). Counting is the process of determining the number of elements of a finite set of objects; \mathcal p(x) \to [0, \infty]$ on $\mathcal p(x)$ is defined for all $e \in \mathcal p(x)$ by $c(e) = |e|$, and the triple. Can somebody. Is Counting A Measurement.
From teachingmama.org
HandsOn Math Activities for Preschoolers Is Counting A Measurement Suppose that s is a finite set. The function # on p(s) is called counting measure. Counting is the process of determining the number of elements of a finite set of objects; That is, determining the size of a set. $\mu (\emptyset) = 0$$\mu (\bigcup \limits_ {k =1}^. Can somebody tell me why the counting measure (so, if $s=p(x)$, then. Is Counting A Measurement.
From www.pinterest.fr
Kindergarten Measurement Worksheets K5 Learning Measurement Is Counting A Measurement For a ⊆ s, the cardinality of a is the number of elements in a, and is denoted #(a). \mathcal p(x) \to [0, \infty]$ on $\mathcal p(x)$ is defined for all $e \in \mathcal p(x)$ by $c(e) = |e|$, and the triple. To count means to determine the cardinality of some finite set. If a ⊆ s then the cardinality. Is Counting A Measurement.
From www.pinterest.co.uk
Pin on Teachers Pay Teachers Is Counting A Measurement Technically, since the natural numbers are usually defined as. To count means to determine the cardinality of some finite set. The function # on p(s) is called counting measure. For a ⊆ s, the cardinality of a is the number of elements in a, and is denoted #(a). \mathcal p(x) \to [0, \infty]$ on $\mathcal p(x)$ is defined for all. Is Counting A Measurement.