Cylinder Equation X Y Z . Recognize the main features of ellipsoids, paraboloids, and hyperboloids. Use traces to draw the. The important thing here is in fact that $z$ does not occur in the equation. Summarizing, the equation of the cylinder is x2 + y2 = r2. If it is, p p. A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. For a given y = k, a. To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan. Recognize the main features of ellipsoids, paraboloids, and hyperboloids. This is the implicit equation of a cylinder: Given a point p = (x1, y1, z1) in space, we need to: A point $(x,y,z)$ lies on the cylinder if it satisfies the equation. (x,y,z) belong to the cylinder iff x2 + y2 = r2 and z constant. Let the coordinates of q be (x0, y0, 0).
from www.chegg.com
For a given y = k, a. This is the implicit equation of a cylinder: Given a point p = (x1, y1, z1) in space, we need to: Summarizing, the equation of the cylinder is x2 + y2 = r2. (x,y,z) belong to the cylinder iff x2 + y2 = r2 and z constant. A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. The important thing here is in fact that $z$ does not occur in the equation. Recognize the main features of ellipsoids, paraboloids, and hyperboloids. A point $(x,y,z)$ lies on the cylinder if it satisfies the equation. To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan.
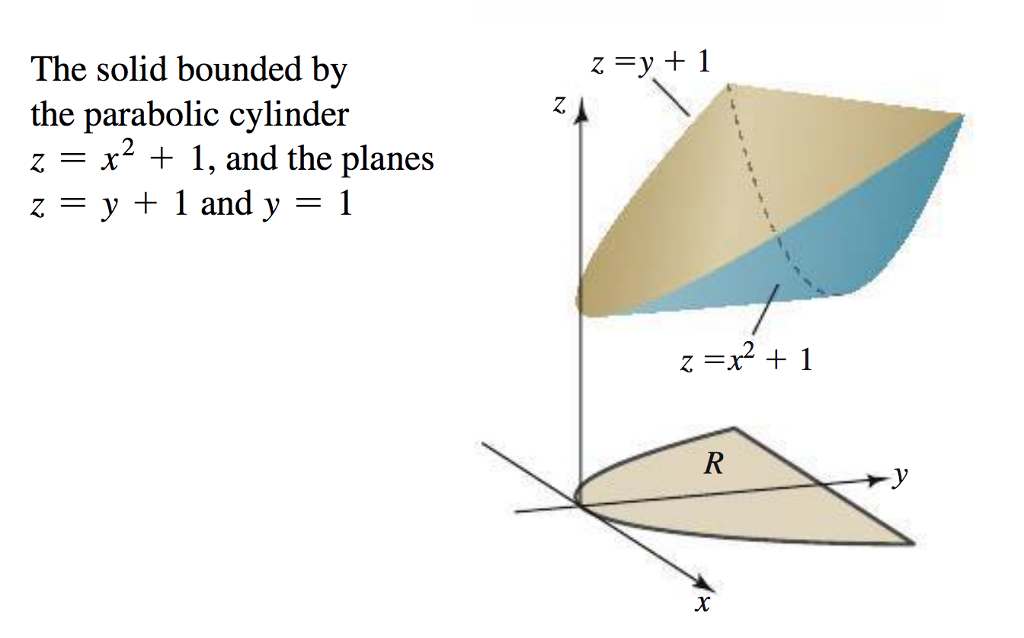
Solved The solid bounded by the parabolic cylinder z = x2 +
Cylinder Equation X Y Z Let the coordinates of q be (x0, y0, 0). To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan. Given a point p = (x1, y1, z1) in space, we need to: Summarizing, the equation of the cylinder is x2 + y2 = r2. For a given y = k, a. The important thing here is in fact that $z$ does not occur in the equation. If it is, p p. Use traces to draw the. (x,y,z) belong to the cylinder iff x2 + y2 = r2 and z constant. A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. Let the coordinates of q be (x0, y0, 0). Recognize the main features of ellipsoids, paraboloids, and hyperboloids. Recognize the main features of ellipsoids, paraboloids, and hyperboloids. A point $(x,y,z)$ lies on the cylinder if it satisfies the equation. This is the implicit equation of a cylinder:
From www.chegg.com
Solved The plane x + y +z = 1 and the cylinder x2 + y2 Cylinder Equation X Y Z To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan. If it is, p p. Given a point p = (x1, y1, z1) in space, we need to: Let the coordinates of q be (x0, y0, 0). This is the implicit equation of a cylinder: (x,y,z) belong to the cylinder iff x2 + y2 = r2. Cylinder Equation X Y Z.
From www.numerade.com
SOLVED A solid E lies within the cylinder x^2 + y^2 = 1, below the Cylinder Equation X Y Z To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan. This is the implicit equation of a cylinder: A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. (x,y,z) belong to the cylinder iff x2 + y2 = r2 and z constant.. Cylinder Equation X Y Z.
From www.chegg.com
Solved The solid bounded by the parabolic cylinder z = x^2 + Cylinder Equation X Y Z Recognize the main features of ellipsoids, paraboloids, and hyperboloids. This is the implicit equation of a cylinder: Use traces to draw the. To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan. For a given y = k, a. Let the coordinates of q be (x0, y0, 0). If it is, p p. A cylinder is. Cylinder Equation X Y Z.
From math.stackexchange.com
calculus What equation describes a cylinder with two points A(X_1, Y Cylinder Equation X Y Z Let the coordinates of q be (x0, y0, 0). A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. Given a point p = (x1, y1, z1) in space, we need to: (x,y,z) belong to the cylinder iff x2 + y2 = r2 and z constant.. Cylinder Equation X Y Z.
From www.chegg.com
Solved (1 point) (a) Find a vector parametric equation for Cylinder Equation X Y Z A point $(x,y,z)$ lies on the cylinder if it satisfies the equation. A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. If it is, p p. Given a point p = (x1, y1, z1) in space, we need to: To convert a point from cartesian. Cylinder Equation X Y Z.
From www.numerade.com
SOLVEDSketch the graph of the cylinder with the given equation. y^2+z^2=9 Cylinder Equation X Y Z A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. Let the coordinates of q be (x0, y0, 0). The important thing here is in fact that $z$ does not occur in the equation. Given a point p = (x1, y1, z1) in space, we need. Cylinder Equation X Y Z.
From www.chegg.com
Solved EXAMPLE 4 Find the volume of the solid that lies Cylinder Equation X Y Z The important thing here is in fact that $z$ does not occur in the equation. Let the coordinates of q be (x0, y0, 0). A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. (x,y,z) belong to the cylinder iff x2 + y2 = r2 and. Cylinder Equation X Y Z.
From www.numerade.com
SOLVEDIn Exercises 15, find an equation in x, y, and z for the graph Cylinder Equation X Y Z If it is, p p. A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. Let the coordinates of q be (x0, y0, 0). To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan. The important thing here is in fact that. Cylinder Equation X Y Z.
From www.youtube.com
Math 212 RS2 Lecture 23 Equations of Lines and Planes; Sketching Cylinder Equation X Y Z If it is, p p. This is the implicit equation of a cylinder: Given a point p = (x1, y1, z1) in space, we need to: Let the coordinates of q be (x0, y0, 0). For a given y = k, a. (x,y,z) belong to the cylinder iff x2 + y2 = r2 and z constant. Use traces to draw. Cylinder Equation X Y Z.
From calcworkshop.com
Quadric Surfaces (Identified and Explained w/ Examples!) Cylinder Equation X Y Z For a given y = k, a. Recognize the main features of ellipsoids, paraboloids, and hyperboloids. Use traces to draw the. A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. Given a point p = (x1, y1, z1) in space, we need to: If it. Cylinder Equation X Y Z.
From www.chegg.com
Solved The solid bounded by the parabolic cylinder z = x2 + Cylinder Equation X Y Z Let the coordinates of q be (x0, y0, 0). The important thing here is in fact that $z$ does not occur in the equation. Summarizing, the equation of the cylinder is x2 + y2 = r2. To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan. For a given y = k, a. If it is,. Cylinder Equation X Y Z.
From blogjpmbahe0amz.blogspot.com
【ベストコレクション】 graph of cylinder x^2 y^2=1 344540 Blogjpmbahe0amz Cylinder Equation X Y Z For a given y = k, a. The important thing here is in fact that $z$ does not occur in the equation. Recognize the main features of ellipsoids, paraboloids, and hyperboloids. Given a point p = (x1, y1, z1) in space, we need to: Recognize the main features of ellipsoids, paraboloids, and hyperboloids. Let the coordinates of q be (x0,. Cylinder Equation X Y Z.
From brainly.in
find the equation of right circular cylinder whose axis is x2=z,y=0 Cylinder Equation X Y Z (x,y,z) belong to the cylinder iff x2 + y2 = r2 and z constant. This is the implicit equation of a cylinder: Recognize the main features of ellipsoids, paraboloids, and hyperboloids. Given a point p = (x1, y1, z1) in space, we need to: Recognize the main features of ellipsoids, paraboloids, and hyperboloids. A point $(x,y,z)$ lies on the cylinder. Cylinder Equation X Y Z.
From www.toppr.com
the value of x, y, z { begin{matrix} x+y+z x+z y+z end{matrix}} quad Cylinder Equation X Y Z (x,y,z) belong to the cylinder iff x2 + y2 = r2 and z constant. To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan. Recognize the main features of ellipsoids, paraboloids, and hyperboloids. A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane. Cylinder Equation X Y Z.
From www.coursehero.com
[Solved] Find a vectorparametric equation r 1( t )= x ( t ) y ( t ) z Cylinder Equation X Y Z Summarizing, the equation of the cylinder is x2 + y2 = r2. A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. This is the implicit equation of a cylinder: To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan. Let the. Cylinder Equation X Y Z.
From www.chegg.com
Solved Describe the surface. x2+z2=8 sphere ellipsoid Cylinder Equation X Y Z Recognize the main features of ellipsoids, paraboloids, and hyperboloids. Summarizing, the equation of the cylinder is x2 + y2 = r2. If it is, p p. Recognize the main features of ellipsoids, paraboloids, and hyperboloids. For a given y = k, a. To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan. Let the coordinates of. Cylinder Equation X Y Z.
From socratic.org
Find the equation of the cylinder whose base is circle x^2+y^2=9, z=0 Cylinder Equation X Y Z This is the implicit equation of a cylinder: A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. Summarizing, the equation of the cylinder is x2 + y2 = r2. Recognize the main features of ellipsoids, paraboloids, and hyperboloids. Let the coordinates of q be (x0,. Cylinder Equation X Y Z.
From www.chegg.com
Solved Find the parameterization of the cylinder x2 + (y Cylinder Equation X Y Z A point $(x,y,z)$ lies on the cylinder if it satisfies the equation. This is the implicit equation of a cylinder: Let the coordinates of q be (x0, y0, 0). Recognize the main features of ellipsoids, paraboloids, and hyperboloids. Recognize the main features of ellipsoids, paraboloids, and hyperboloids. Given a point p = (x1, y1, z1) in space, we need to:. Cylinder Equation X Y Z.
From www.alamy.com
Right circular cylinder formula. vector Stock Vector Image & Art Alamy Cylinder Equation X Y Z Recognize the main features of ellipsoids, paraboloids, and hyperboloids. This is the implicit equation of a cylinder: A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. (x,y,z) belong to the cylinder iff x2 + y2 = r2 and z constant. A point $(x,y,z)$ lies on. Cylinder Equation X Y Z.
From www.youtube.com
Curve of Intersection of Two Surfaces in 3D Plane and a Cylinder YouTube Cylinder Equation X Y Z If it is, p p. Given a point p = (x1, y1, z1) in space, we need to: (x,y,z) belong to the cylinder iff x2 + y2 = r2 and z constant. A point $(x,y,z)$ lies on the cylinder if it satisfies the equation. For a given y = k, a. Summarizing, the equation of the cylinder is x2 +. Cylinder Equation X Y Z.
From www.teachoo.com
Example 32 Show that Determinant = 2xyz (x + y + z)^3 Class 12 Cylinder Equation X Y Z This is the implicit equation of a cylinder: Recognize the main features of ellipsoids, paraboloids, and hyperboloids. Use traces to draw the. Summarizing, the equation of the cylinder is x2 + y2 = r2. (x,y,z) belong to the cylinder iff x2 + y2 = r2 and z constant. For a given y = k, a. Let the coordinates of q. Cylinder Equation X Y Z.
From www.numerade.com
EXAMPLE 6 Find vector function that represents the curve of Cylinder Equation X Y Z For a given y = k, a. Given a point p = (x1, y1, z1) in space, we need to: Use traces to draw the. Recognize the main features of ellipsoids, paraboloids, and hyperboloids. Summarizing, the equation of the cylinder is x2 + y2 = r2. To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan.. Cylinder Equation X Y Z.
From www.youtube.com
Solve the Equation x^y = y^x YouTube Cylinder Equation X Y Z Recognize the main features of ellipsoids, paraboloids, and hyperboloids. To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan. Use traces to draw the. Summarizing, the equation of the cylinder is x2 + y2 = r2. Given a point p = (x1, y1, z1) in space, we need to: This is the implicit equation of a. Cylinder Equation X Y Z.
From www.pinterest.co.uk
In this video I go over an example on graphing a circle and a cylinder Cylinder Equation X Y Z Let the coordinates of q be (x0, y0, 0). This is the implicit equation of a cylinder: A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. If it is, p p. For a given y = k, a. Given a point p = (x1, y1,. Cylinder Equation X Y Z.
From www.chegg.com
Solved Consider the cone. Give the equation and describe the Cylinder Equation X Y Z A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. Summarizing, the equation of the cylinder is x2 + y2 = r2. To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan. The important thing here is in fact that $z$ does. Cylinder Equation X Y Z.
From www.chegg.com
Solved The cylinder x2 + y2 = 1 intersects the plane x + z = Cylinder Equation X Y Z This is the implicit equation of a cylinder: Given a point p = (x1, y1, z1) in space, we need to: If it is, p p. Summarizing, the equation of the cylinder is x2 + y2 = r2. Let the coordinates of q be (x0, y0, 0). Recognize the main features of ellipsoids, paraboloids, and hyperboloids. The important thing here. Cylinder Equation X Y Z.
From www.youtube.com
Equation of a Cylinder in 3D (THREE DIMENSIONS) YouTube Cylinder Equation X Y Z Use traces to draw the. For a given y = k, a. (x,y,z) belong to the cylinder iff x2 + y2 = r2 and z constant. This is the implicit equation of a cylinder: Recognize the main features of ellipsoids, paraboloids, and hyperboloids. Let the coordinates of q be (x0, y0, 0). Summarizing, the equation of the cylinder is x2. Cylinder Equation X Y Z.
From blogjpmbahe0amz.blogspot.com
【ベストコレクション】 graph of cylinder x^2 y^2=1 344540 Blogjpmbahe0amz Cylinder Equation X Y Z For a given y = k, a. Recognize the main features of ellipsoids, paraboloids, and hyperboloids. Let the coordinates of q be (x0, y0, 0). Use traces to draw the. The important thing here is in fact that $z$ does not occur in the equation. A point $(x,y,z)$ lies on the cylinder if it satisfies the equation. Recognize the main. Cylinder Equation X Y Z.
From www.chegg.com
Solved EXAMPLE 1 EvaluateF dr, where F(x, y, z) 4y2i Cylinder Equation X Y Z If it is, p p. Recognize the main features of ellipsoids, paraboloids, and hyperboloids. This is the implicit equation of a cylinder: Given a point p = (x1, y1, z1) in space, we need to: Let the coordinates of q be (x0, y0, 0). Summarizing, the equation of the cylinder is x2 + y2 = r2. (x,y,z) belong to the. Cylinder Equation X Y Z.
From www.chegg.com
Solved EXAMPLE 6 Find a vector function that represents the Cylinder Equation X Y Z Recognize the main features of ellipsoids, paraboloids, and hyperboloids. A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. (x,y,z) belong to the cylinder iff x2 + y2 = r2 and z constant. If it is, p p. Given a point p = (x1, y1, z1). Cylinder Equation X Y Z.
From www.chegg.com
Solved EXAMPLE 3 A solid E lies within the cylinder x2 + y2 Cylinder Equation X Y Z A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. (x,y,z) belong to the cylinder iff x2 + y2 = r2 and z constant. This is the implicit equation of a cylinder: For a given y = k, a. Recognize the main features of ellipsoids, paraboloids,. Cylinder Equation X Y Z.
From www.chegg.com
Solved Find the vector equation that represents the curve of Cylinder Equation X Y Z A cylinder is a surface that consists of all lines that are parallel to a given line and pass through a given plane curve. Recognize the main features of ellipsoids, paraboloids, and hyperboloids. To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan. The important thing here is in fact that $z$ does not occur in. Cylinder Equation X Y Z.
From www.chegg.com
Solved where F(x, y, z) = (2x,2y,22 ), S cylinder x2 +y2 = Cylinder Equation X Y Z A point $(x,y,z)$ lies on the cylinder if it satisfies the equation. Use traces to draw the. The important thing here is in fact that $z$ does not occur in the equation. To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan. (x,y,z) belong to the cylinder iff x2 + y2 = r2 and z constant.. Cylinder Equation X Y Z.
From www.numerade.com
SOLVEDSketch the graph of the cylinder with the given equation. y^2+z^2=9 Cylinder Equation X Y Z Let the coordinates of q be (x0, y0, 0). Recognize the main features of ellipsoids, paraboloids, and hyperboloids. For a given y = k, a. If it is, p p. To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan. Given a point p = (x1, y1, z1) in space, we need to: The important thing. Cylinder Equation X Y Z.
From www.youtube.com
Vector Equation of Curve of Intersection of a Plane and Cylinder Cylinder Equation X Y Z Summarizing, the equation of the cylinder is x2 + y2 = r2. A point $(x,y,z)$ lies on the cylinder if it satisfies the equation. This is the implicit equation of a cylinder: For a given y = k, a. The important thing here is in fact that $z$ does not occur in the equation. If it is, p p. Use. Cylinder Equation X Y Z.