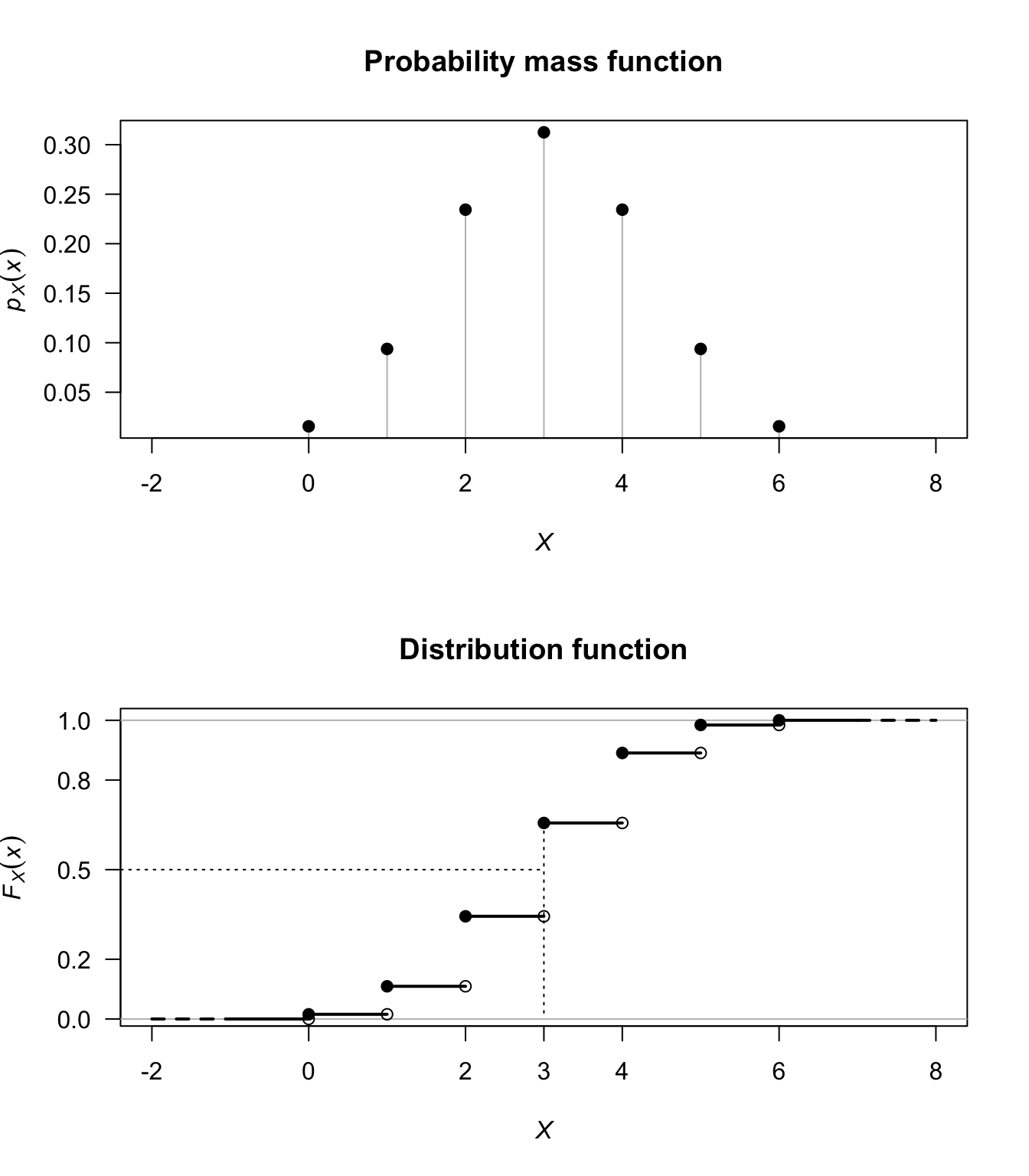
Distribution Function Technique . We find the region in x1,x2,x3,.xn space such that φ(x1, x2,.xn) ≤ φ. Distributions of functions of random variables. We’ll break down the formulas, understand their characteristics, and make it easy to grasp how they help with data. $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ We can then find the probability that. The empirical distribution function is simply fb n(x) = 1 n ×( the number of xi ≤ x). Ex 3 comes from the following corollary, a special case of theorem 5.1. One approach to finding the probability distribution of a function of a random variable relies on the relationship between the pdf and cdf for a continuous random variable: In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different types, and how they’re used. For example, we used the distribution function technique to show that: Let x1,.,xn have the distribution f∈ m.
from bookdown.org
We can then find the probability that. We find the region in x1,x2,x3,.xn space such that φ(x1, x2,.xn) ≤ φ. One approach to finding the probability distribution of a function of a random variable relies on the relationship between the pdf and cdf for a continuous random variable: $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ Let x1,.,xn have the distribution f∈ m. We’ll break down the formulas, understand their characteristics, and make it easy to grasp how they help with data. For example, we used the distribution function technique to show that: Ex 3 comes from the following corollary, a special case of theorem 5.1. Distributions of functions of random variables. The empirical distribution function is simply fb n(x) = 1 n ×( the number of xi ≤ x).
3 Mathematical expectation Distribution Theory
Distribution Function Technique Let x1,.,xn have the distribution f∈ m. We find the region in x1,x2,x3,.xn space such that φ(x1, x2,.xn) ≤ φ. Let x1,.,xn have the distribution f∈ m. In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different types, and how they’re used. For example, we used the distribution function technique to show that: We’ll break down the formulas, understand their characteristics, and make it easy to grasp how they help with data. $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ One approach to finding the probability distribution of a function of a random variable relies on the relationship between the pdf and cdf for a continuous random variable: The empirical distribution function is simply fb n(x) = 1 n ×( the number of xi ≤ x). Distributions of functions of random variables. Ex 3 comes from the following corollary, a special case of theorem 5.1. We can then find the probability that.
From mmlpi.ch
Pair Distribution Function Distribution Function Technique The empirical distribution function is simply fb n(x) = 1 n ×( the number of xi ≤ x). We can then find the probability that. One approach to finding the probability distribution of a function of a random variable relies on the relationship between the pdf and cdf for a continuous random variable: Let x1,.,xn have the distribution f∈ m.. Distribution Function Technique.
From www.slideserve.com
PPT Chapter 8 RandomVariate Generation PowerPoint Presentation, free Distribution Function Technique Distributions of functions of random variables. For example, we used the distribution function technique to show that: In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different types, and how they’re used. We find the region in x1,x2,x3,.xn space such that φ(x1, x2,.xn) ≤ φ. The empirical distribution function is simply fb n(x) = 1. Distribution Function Technique.
From www.researchgate.net
2 The probability distribution function f (x) (solid line) and the Distribution Function Technique We find the region in x1,x2,x3,.xn space such that φ(x1, x2,.xn) ≤ φ. Let x1,.,xn have the distribution f∈ m. We can then find the probability that. For example, we used the distribution function technique to show that: In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different types, and how they’re used. $$\frac{d}{dx} [f(x)]. Distribution Function Technique.
From www.slideserve.com
PPT Chapter 5 Functions of Random Variables PowerPoint Presentation Distribution Function Technique Distributions of functions of random variables. For example, we used the distribution function technique to show that: The empirical distribution function is simply fb n(x) = 1 n ×( the number of xi ≤ x). We find the region in x1,x2,x3,.xn space such that φ(x1, x2,.xn) ≤ φ. $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ Let x1,.,xn have. Distribution Function Technique.
From artvda.mystrikingly.com
Standard normal distribution loss function table negati... Distribution Function Technique Distributions of functions of random variables. Let x1,.,xn have the distribution f∈ m. The empirical distribution function is simply fb n(x) = 1 n ×( the number of xi ≤ x). For example, we used the distribution function technique to show that: One approach to finding the probability distribution of a function of a random variable relies on the relationship. Distribution Function Technique.
From www.chegg.com
Solved 16. Suppose the cumulative distribution function of a Distribution Function Technique We’ll break down the formulas, understand their characteristics, and make it easy to grasp how they help with data. $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ The empirical distribution function is simply fb n(x) = 1 n ×( the number of xi ≤ x). In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their. Distribution Function Technique.
From www.chegg.com
Using the distribution function technique or change Distribution Function Technique Ex 3 comes from the following corollary, a special case of theorem 5.1. One approach to finding the probability distribution of a function of a random variable relies on the relationship between the pdf and cdf for a continuous random variable: We can then find the probability that. Distributions of functions of random variables. We’ll break down the formulas, understand. Distribution Function Technique.
From www.chegg.com
Solved Moment Generating Functions (a) Let X1, . . . , Xn be Distribution Function Technique We can then find the probability that. We find the region in x1,x2,x3,.xn space such that φ(x1, x2,.xn) ≤ φ. In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different types, and how they’re used. For example, we used the distribution function technique to show that: Ex 3 comes from the following corollary, a special. Distribution Function Technique.
From www.semanticscholar.org
Figure 3 from Copyright©JCPDS International Centre for Diffraction Distribution Function Technique Ex 3 comes from the following corollary, a special case of theorem 5.1. In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different types, and how they’re used. We find the region in x1,x2,x3,.xn space such that φ(x1, x2,.xn) ≤ φ. The empirical distribution function is simply fb n(x) = 1 n ×( the number. Distribution Function Technique.
From journals.iucr.org
(IUCr) Modelling and validation of particle size distributions of Distribution Function Technique We can then find the probability that. We find the region in x1,x2,x3,.xn space such that φ(x1, x2,.xn) ≤ φ. Let x1,.,xn have the distribution f∈ m. $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different types, and how they’re used. Distributions of functions of. Distribution Function Technique.
From www.chegg.com
Solved Prove it using distribution function technique or Distribution Function Technique Distributions of functions of random variables. We find the region in x1,x2,x3,.xn space such that φ(x1, x2,.xn) ≤ φ. $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ Let x1,.,xn have the distribution f∈ m. We can then find the probability that. Ex 3 comes from the following corollary, a special case of theorem 5.1. The empirical distribution function is. Distribution Function Technique.
From www.numerade.com
SOLVED Q1. X is an exponential distribution with the parameter theta Distribution Function Technique For example, we used the distribution function technique to show that: We can then find the probability that. The empirical distribution function is simply fb n(x) = 1 n ×( the number of xi ≤ x). We’ll break down the formulas, understand their characteristics, and make it easy to grasp how they help with data. Distributions of functions of random. Distribution Function Technique.
From www.numerade.com
SOLVED If X has an exponential distribution with mean B, use the Distribution Function Technique Ex 3 comes from the following corollary, a special case of theorem 5.1. $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ We can then find the probability that. In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different types, and how they’re used. The empirical distribution function is simply fb n(x) = 1 n. Distribution Function Technique.
From www.youtube.com
Bivariate distributions cumulative distribution functions YouTube Distribution Function Technique We find the region in x1,x2,x3,.xn space such that φ(x1, x2,.xn) ≤ φ. One approach to finding the probability distribution of a function of a random variable relies on the relationship between the pdf and cdf for a continuous random variable: $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ Ex 3 comes from the following corollary, a special case. Distribution Function Technique.
From www.researchgate.net
Empirical distribution function along the X axis and theoretical Distribution Function Technique One approach to finding the probability distribution of a function of a random variable relies on the relationship between the pdf and cdf for a continuous random variable: We can then find the probability that. We’ll break down the formulas, understand their characteristics, and make it easy to grasp how they help with data. Distributions of functions of random variables.. Distribution Function Technique.
From artvda.mystrikingly.com
Standard normal distribution loss function table negati... Distribution Function Technique We can then find the probability that. $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ For example, we used the distribution function technique to show that: The empirical distribution function is simply fb n(x) = 1 n ×( the number of xi ≤ x). In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different. Distribution Function Technique.
From www.numerade.com
SOLVEDIf X has the uniform density with the parameters α=0 and β=1 Distribution Function Technique For example, we used the distribution function technique to show that: The empirical distribution function is simply fb n(x) = 1 n ×( the number of xi ≤ x). We can then find the probability that. We find the region in x1,x2,x3,.xn space such that φ(x1, x2,.xn) ≤ φ. Distributions of functions of random variables. In this article, we’ll look. Distribution Function Technique.
From www.youtube.com
Probability Distribution Functions EXPLAINED! YouTube Distribution Function Technique In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different types, and how they’re used. $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ Let x1,.,xn have the distribution f∈ m. The empirical distribution function is simply fb n(x) = 1 n ×( the number of xi ≤ x). We find the region in x1,x2,x3,.xn. Distribution Function Technique.
From www.chegg.com
Solved 4. Use the distribution function technique to find Distribution Function Technique For example, we used the distribution function technique to show that: One approach to finding the probability distribution of a function of a random variable relies on the relationship between the pdf and cdf for a continuous random variable: The empirical distribution function is simply fb n(x) = 1 n ×( the number of xi ≤ x). Let x1,.,xn have. Distribution Function Technique.
From www.slideserve.com
PPT Multivariable Distributions PowerPoint Presentation, free Distribution Function Technique The empirical distribution function is simply fb n(x) = 1 n ×( the number of xi ≤ x). Ex 3 comes from the following corollary, a special case of theorem 5.1. $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different types, and how they’re used.. Distribution Function Technique.
From www.slideserve.com
PPT Chapter 5 Functions of Random Variables PowerPoint Presentation Distribution Function Technique For example, we used the distribution function technique to show that: Let x1,.,xn have the distribution f∈ m. $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ One approach to finding the probability distribution of a function of a random variable relies on the relationship between the pdf and cdf for a continuous random variable: Ex 3 comes from the. Distribution Function Technique.
From www.numerade.com
SOLVED 7.3 (3 points If X has the uniform density with the parameters Distribution Function Technique Let x1,.,xn have the distribution f∈ m. In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different types, and how they’re used. We’ll break down the formulas, understand their characteristics, and make it easy to grasp how they help with data. Ex 3 comes from the following corollary, a special case of theorem 5.1. For. Distribution Function Technique.
From www.youtube.com
Cumulative distribution function technique YouTube Distribution Function Technique The empirical distribution function is simply fb n(x) = 1 n ×( the number of xi ≤ x). One approach to finding the probability distribution of a function of a random variable relies on the relationship between the pdf and cdf for a continuous random variable: Let x1,.,xn have the distribution f∈ m. In this article, we’ll look into probability. Distribution Function Technique.
From www.slideserve.com
PPT Continuous distributions PowerPoint Presentation, free download Distribution Function Technique In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different types, and how they’re used. We find the region in x1,x2,x3,.xn space such that φ(x1, x2,.xn) ≤ φ. $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ Distributions of functions of random variables. For example, we used the distribution function technique to show that: Let. Distribution Function Technique.
From bookdown.org
3 Mathematical expectation Distribution Theory Distribution Function Technique In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different types, and how they’re used. The empirical distribution function is simply fb n(x) = 1 n ×( the number of xi ≤ x). $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ Let x1,.,xn have the distribution f∈ m. For example, we used the distribution. Distribution Function Technique.
From www.youtube.com
Mathematical StatisticsCumulative Distribution Function technique Distribution Function Technique We can then find the probability that. We find the region in x1,x2,x3,.xn space such that φ(x1, x2,.xn) ≤ φ. For example, we used the distribution function technique to show that: In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different types, and how they’re used. One approach to finding the probability distribution of a. Distribution Function Technique.
From www.semanticscholar.org
[PDF] APPROXIMATIONS TO THE NORMAL DISTRIBUTION FUNCTION AND AN Distribution Function Technique In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different types, and how they’re used. We can then find the probability that. For example, we used the distribution function technique to show that: We’ll break down the formulas, understand their characteristics, and make it easy to grasp how they help with data. Ex 3 comes. Distribution Function Technique.
From www.youtube.com
Moment generating function technique YouTube Distribution Function Technique For example, we used the distribution function technique to show that: Let x1,.,xn have the distribution f∈ m. Distributions of functions of random variables. Ex 3 comes from the following corollary, a special case of theorem 5.1. In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different types, and how they’re used. One approach to. Distribution Function Technique.
From www.chegg.com
Solved 1. Use the distribution function technique to find Distribution Function Technique We can then find the probability that. For example, we used the distribution function technique to show that: We find the region in x1,x2,x3,.xn space such that φ(x1, x2,.xn) ≤ φ. Distributions of functions of random variables. $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ One approach to finding the probability distribution of a function of a random variable. Distribution Function Technique.
From www.youtube.com
Cumulative distribution technique Example 4 YouTube Distribution Function Technique We can then find the probability that. Distributions of functions of random variables. For example, we used the distribution function technique to show that: We’ll break down the formulas, understand their characteristics, and make it easy to grasp how they help with data. We find the region in x1,x2,x3,.xn space such that φ(x1, x2,.xn) ≤ φ. One approach to finding. Distribution Function Technique.
From www.amazon.science
Improving forecasting by learning quantile functions Amazon Science Distribution Function Technique Distributions of functions of random variables. For example, we used the distribution function technique to show that: The empirical distribution function is simply fb n(x) = 1 n ×( the number of xi ≤ x). One approach to finding the probability distribution of a function of a random variable relies on the relationship between the pdf and cdf for a. Distribution Function Technique.
From www.youtube.com
Cumulative distribution technique Example 1 YouTube Distribution Function Technique Let x1,.,xn have the distribution f∈ m. $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ Ex 3 comes from the following corollary, a special case of theorem 5.1. We can then find the probability that. For example, we used the distribution function technique to show that: We’ll break down the formulas, understand their characteristics, and make it easy to. Distribution Function Technique.
From www.numerade.com
SOLVED If X has the uniform density with the parameters α = 0 and β Distribution Function Technique In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different types, and how they’re used. $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ The empirical distribution function is simply fb n(x) = 1 n ×( the number of xi ≤ x). Ex 3 comes from the following corollary, a special case of theorem 5.1.. Distribution Function Technique.
From www.researchgate.net
Cumulative Distribution Function (CDF) and Probability Mass Function Distribution Function Technique For example, we used the distribution function technique to show that: In this article, we’ll look into probability distribution functions (pdfs), distribution functions and their different types, and how they’re used. We find the region in x1,x2,x3,.xn space such that φ(x1, x2,.xn) ≤ φ. Distributions of functions of random variables. The empirical distribution function is simply fb n(x) = 1. Distribution Function Technique.
From www.youtube.com
Section 5 1 Distribution Function Technique YouTube Distribution Function Technique The empirical distribution function is simply fb n(x) = 1 n ×( the number of xi ≤ x). $$\frac{d}{dx} [f(x)] = f(x) \qquad\text{''derivative of cdf = pdf}\notag$$ Let x1,.,xn have the distribution f∈ m. We can then find the probability that. We find the region in x1,x2,x3,.xn space such that φ(x1, x2,.xn) ≤ φ. One approach to finding the probability. Distribution Function Technique.