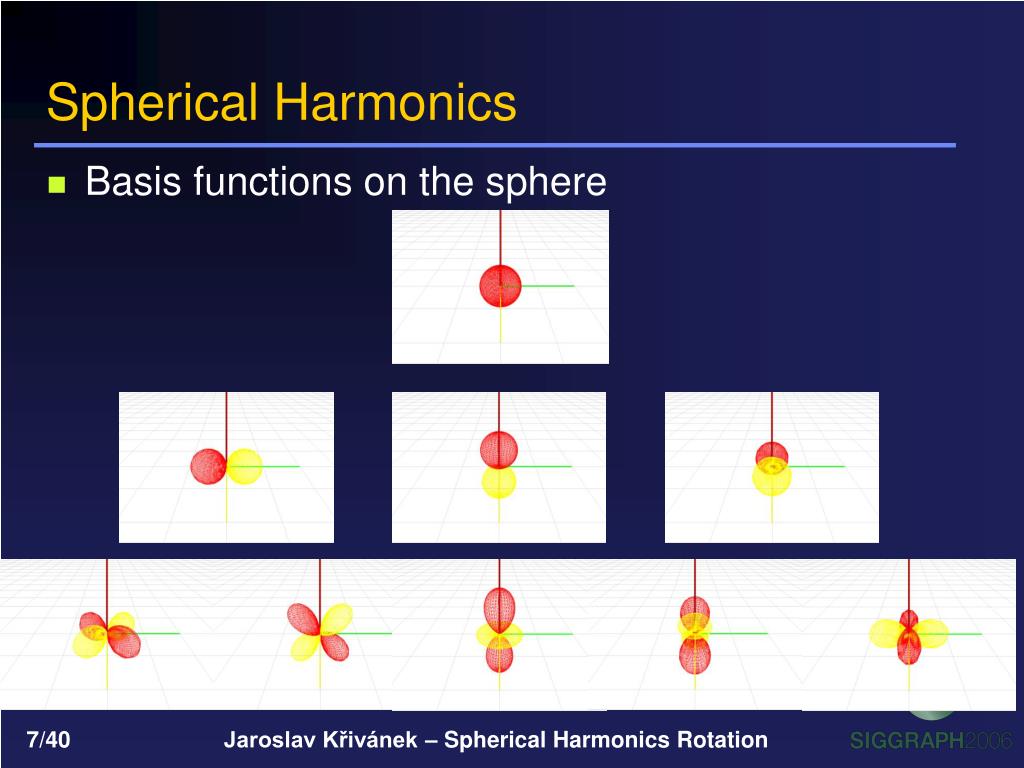
Spherical Harmonics Meaning In Physics at Darcy Parnell blog

Spherical Harmonics Meaning In Physics. Spherical harmonics form an orthogonal family: The simultaneous eigenstates, \ (y_ {l,m} (\theta,\phi)\), of \ (l^2\) and \ (l_z\) are known as the spherical harmonics. Let us investigate their functional form. Spherical harmonics are a set of functions used to represent functions on the surface of the sphere \ (s^2\). (ym l, y k n) = s(1) ∫d2sˆ ym l (sˆ)yk n(sˆ)∗=0, m≠k or l≠n.(14) we usually scale the spherical. Spherical harmonics are used extremely widely in physics. Spherical harmonics are a set of mathematical functions that define the angular portion of a function on the surface of a sphere. Circle, but we could equally well call it a sphere and say the fourier series are spherical harmonics. We know that \ [l_+\,y_ {l,l} (\theta,\phi) = 0,\] because there is no state for which \ (m\) has a larger value than \ (+l\). (12) for some choice of coefficients aℓm. The usual usage for spherical. You will see them soon enough in quantum mechanics, they are front and centre.

You will see them soon enough in quantum mechanics, they are front and centre. (12) for some choice of coefficients aℓm. The simultaneous eigenstates, \ (y_ {l,m} (\theta,\phi)\), of \ (l^2\) and \ (l_z\) are known as the spherical harmonics. Spherical harmonics are used extremely widely in physics. Spherical harmonics are a set of mathematical functions that define the angular portion of a function on the surface of a sphere. Let us investigate their functional form. Circle, but we could equally well call it a sphere and say the fourier series are spherical harmonics. (ym l, y k n) = s(1) ∫d2sˆ ym l (sˆ)yk n(sˆ)∗=0, m≠k or l≠n.(14) we usually scale the spherical. The usual usage for spherical. Spherical harmonics form an orthogonal family:

PPT Fast Approximation to Spherical Harmonics Rotation PowerPoint

Spherical Harmonics Meaning In Physics (12) for some choice of coefficients aℓm. (12) for some choice of coefficients aℓm. Spherical harmonics are a set of mathematical functions that define the angular portion of a function on the surface of a sphere. You will see them soon enough in quantum mechanics, they are front and centre. Spherical harmonics form an orthogonal family: Circle, but we could equally well call it a sphere and say the fourier series are spherical harmonics. (ym l, y k n) = s(1) ∫d2sˆ ym l (sˆ)yk n(sˆ)∗=0, m≠k or l≠n.(14) we usually scale the spherical. Let us investigate their functional form. The simultaneous eigenstates, \ (y_ {l,m} (\theta,\phi)\), of \ (l^2\) and \ (l_z\) are known as the spherical harmonics. Spherical harmonics are a set of functions used to represent functions on the surface of the sphere \ (s^2\). The usual usage for spherical. We know that \ [l_+\,y_ {l,l} (\theta,\phi) = 0,\] because there is no state for which \ (m\) has a larger value than \ (+l\). Spherical harmonics are used extremely widely in physics.