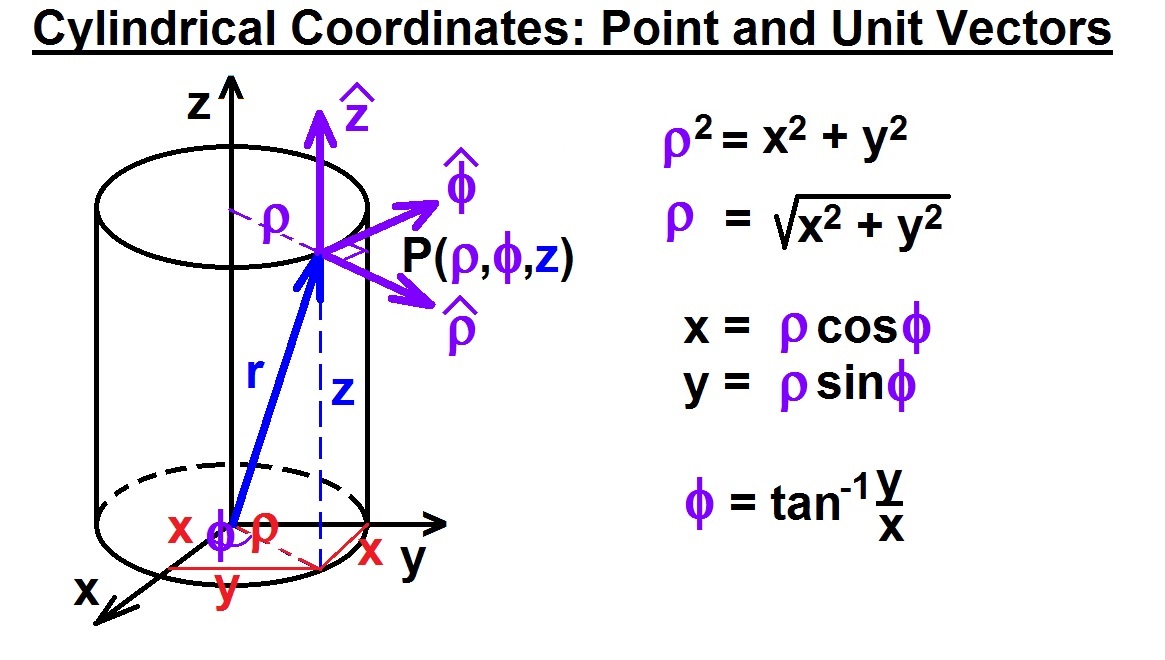
X Hat In Cylindrical Coordinates at Logan Oldaker blog

X Hat In Cylindrical Coordinates. The position of any point in a cylindrical coordinate system is written as \ [ {\bf r} = r \; This tutorial will denote vector quantities with an arrow atop a letter, except unit vectors that define coordinate systems which will have a hat. \hat {\bf z} \] where \ (\hat {\bf r} = (\cos \theta,. The length of the hypotenuse is r and. The cylindrical coordinate system extends polar coordinates into 3d by using the standard vertical coordinate $z$. In the cylindrical coordinate system, a point in space (figure 12.7.1) is represented by the ordered triple (r, θ, z), where. $\begingroup$ if iim not mistaking, you are asking for an expression of cartesian coordinates $(x, y, z)$ in terms of cylindrical coordinates $(r, \theta, z)$. (ρ, φ, z) is given in cartesian coordinates by: \hat {\bf r} + z \; Vectors are defined in cylindrical coordinates by (ρ, φ, z), where.

This tutorial will denote vector quantities with an arrow atop a letter, except unit vectors that define coordinate systems which will have a hat. The position of any point in a cylindrical coordinate system is written as \ [ {\bf r} = r \; The length of the hypotenuse is r and. (ρ, φ, z) is given in cartesian coordinates by: Vectors are defined in cylindrical coordinates by (ρ, φ, z), where. \hat {\bf r} + z \; In the cylindrical coordinate system, a point in space (figure 12.7.1) is represented by the ordered triple (r, θ, z), where. $\begingroup$ if iim not mistaking, you are asking for an expression of cartesian coordinates $(x, y, z)$ in terms of cylindrical coordinates $(r, \theta, z)$. \hat {\bf z} \] where \ (\hat {\bf r} = (\cos \theta,. The cylindrical coordinate system extends polar coordinates into 3d by using the standard vertical coordinate $z$.

Cylindrical Vector at Collection of Cylindrical

X Hat In Cylindrical Coordinates Vectors are defined in cylindrical coordinates by (ρ, φ, z), where. This tutorial will denote vector quantities with an arrow atop a letter, except unit vectors that define coordinate systems which will have a hat. \hat {\bf r} + z \; \hat {\bf z} \] where \ (\hat {\bf r} = (\cos \theta,. Vectors are defined in cylindrical coordinates by (ρ, φ, z), where. $\begingroup$ if iim not mistaking, you are asking for an expression of cartesian coordinates $(x, y, z)$ in terms of cylindrical coordinates $(r, \theta, z)$. The cylindrical coordinate system extends polar coordinates into 3d by using the standard vertical coordinate $z$. In the cylindrical coordinate system, a point in space (figure 12.7.1) is represented by the ordered triple (r, θ, z), where. The length of the hypotenuse is r and. (ρ, φ, z) is given in cartesian coordinates by: The position of any point in a cylindrical coordinate system is written as \ [ {\bf r} = r \;