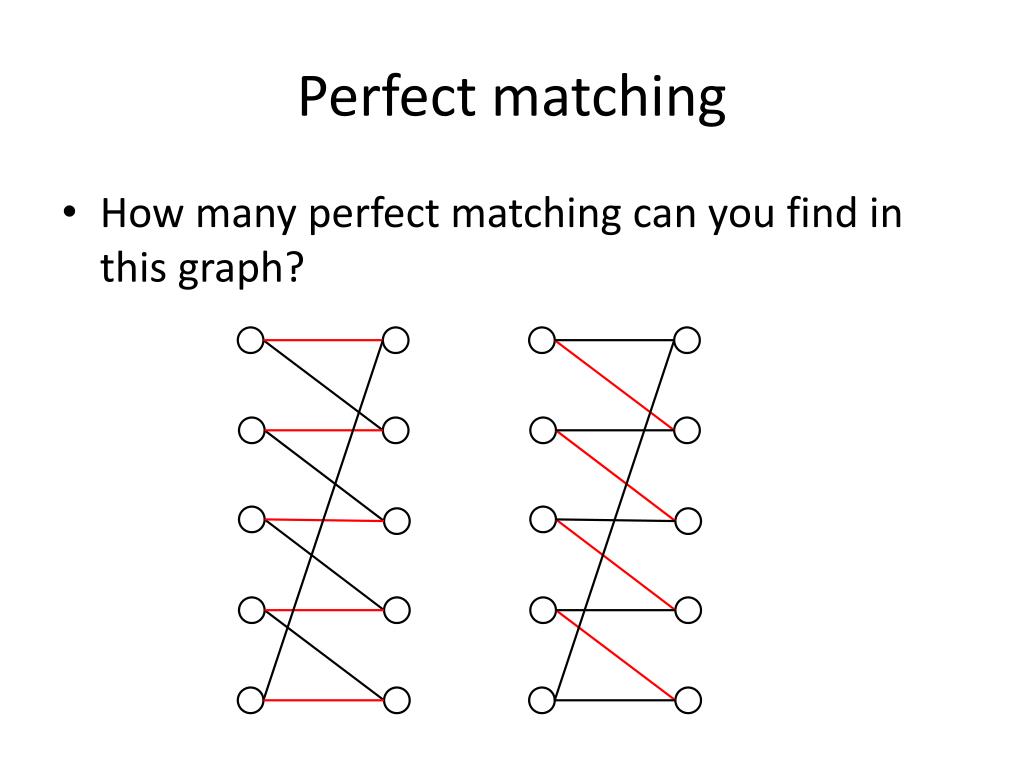
Define Matching Graph . Simply, there should not be any common vertex. A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share a vertex in. De nition 1 a matching m in a graph g(v;e) is a subset of the edge set e such that no two edges in m are incident on the same vertex, i.e. A matching graph is a subgraph of a graph where there are no edges adjacent to each other. A matching of graph g is a subgraph of g such that every edge shares no vertex with any other edge. That is, each vertex in. A perfect matching in a graph g is a matching in which every vertex of g appears exactly once, that is, a matching of size exactly n=2.
from www.slideserve.com
A perfect matching in a graph g is a matching in which every vertex of g appears exactly once, that is, a matching of size exactly n=2. A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share a vertex in. That is, each vertex in. De nition 1 a matching m in a graph g(v;e) is a subset of the edge set e such that no two edges in m are incident on the same vertex, i.e. A matching graph is a subgraph of a graph where there are no edges adjacent to each other. Simply, there should not be any common vertex. A matching of graph g is a subgraph of g such that every edge shares no vertex with any other edge.
PPT Discrete Mathematics Tutorial 13 PowerPoint Presentation, free download ID3073522
Define Matching Graph Simply, there should not be any common vertex. A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share a vertex in. A matching of graph g is a subgraph of g such that every edge shares no vertex with any other edge. A perfect matching in a graph g is a matching in which every vertex of g appears exactly once, that is, a matching of size exactly n=2. A matching graph is a subgraph of a graph where there are no edges adjacent to each other. That is, each vertex in. De nition 1 a matching m in a graph g(v;e) is a subset of the edge set e such that no two edges in m are incident on the same vertex, i.e. Simply, there should not be any common vertex.
From brilliant.org
Matching (Graph Theory) Brilliant Math & Science Wiki Define Matching Graph That is, each vertex in. A perfect matching in a graph g is a matching in which every vertex of g appears exactly once, that is, a matching of size exactly n=2. De nition 1 a matching m in a graph g(v;e) is a subset of the edge set e such that no two edges in m are incident on. Define Matching Graph.
From study.com
Matching Graphs with Polynomial Functions Algebra Define Matching Graph De nition 1 a matching m in a graph g(v;e) is a subset of the edge set e such that no two edges in m are incident on the same vertex, i.e. A perfect matching in a graph g is a matching in which every vertex of g appears exactly once, that is, a matching of size exactly n=2. A. Define Matching Graph.
From brainly.com
Match the graph with its function Define Matching Graph That is, each vertex in. A matching of graph g is a subgraph of g such that every edge shares no vertex with any other edge. A perfect matching in a graph g is a matching in which every vertex of g appears exactly once, that is, a matching of size exactly n=2. A matching, also called an independent edge. Define Matching Graph.
From www.youtube.com
Matching Graphs to Equations YouTube Define Matching Graph A perfect matching in a graph g is a matching in which every vertex of g appears exactly once, that is, a matching of size exactly n=2. Simply, there should not be any common vertex. A matching graph is a subgraph of a graph where there are no edges adjacent to each other. A matching, also called an independent edge. Define Matching Graph.
From www.slideserve.com
PPT Node Similarity, Graph Similarity and Matching Theory and Applications PowerPoint Define Matching Graph A perfect matching in a graph g is a matching in which every vertex of g appears exactly once, that is, a matching of size exactly n=2. De nition 1 a matching m in a graph g(v;e) is a subset of the edge set e such that no two edges in m are incident on the same vertex, i.e. A. Define Matching Graph.
From www.youtube.com
6 6 Matching Graphs to their equations 1 YouTube Define Matching Graph Simply, there should not be any common vertex. A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share a vertex in. A perfect matching in a graph g is a matching in which every vertex of g appears exactly once, that is, a matching of size exactly. Define Matching Graph.
From www.slideserve.com
PPT Linear Motion PowerPoint Presentation ID1242638 Define Matching Graph A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share a vertex in. Simply, there should not be any common vertex. A matching of graph g is a subgraph of g such that every edge shares no vertex with any other edge. A perfect matching in a. Define Matching Graph.
From brilliant.org
Matching (Graph Theory) Brilliant Math & Science Wiki Define Matching Graph De nition 1 a matching m in a graph g(v;e) is a subset of the edge set e such that no two edges in m are incident on the same vertex, i.e. That is, each vertex in. Simply, there should not be any common vertex. A perfect matching in a graph g is a matching in which every vertex of. Define Matching Graph.
From pj-fuakgio-ho.blogspot.com
37 matching graphs of functions and their derivatives worksheet Worksheet For Fun Define Matching Graph A matching graph is a subgraph of a graph where there are no edges adjacent to each other. A matching of graph g is a subgraph of g such that every edge shares no vertex with any other edge. Simply, there should not be any common vertex. A perfect matching in a graph g is a matching in which every. Define Matching Graph.
From www.vernier.com
Can I do Graph Matching with Graphical Analysis or Graphical Analysis Pro? Technical Define Matching Graph Simply, there should not be any common vertex. A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share a vertex in. A perfect matching in a graph g is a matching in which every vertex of g appears exactly once, that is, a matching of size exactly. Define Matching Graph.
From rosalind.info
ROSALIND Glossary Perfect matching Define Matching Graph That is, each vertex in. A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share a vertex in. A matching graph is a subgraph of a graph where there are no edges adjacent to each other. A matching of graph g is a subgraph of g such. Define Matching Graph.
From www.slideserve.com
PPT Graph Matching PowerPoint Presentation, free download ID2306645 Define Matching Graph A matching graph is a subgraph of a graph where there are no edges adjacent to each other. A matching of graph g is a subgraph of g such that every edge shares no vertex with any other edge. De nition 1 a matching m in a graph g(v;e) is a subset of the edge set e such that no. Define Matching Graph.
From www.youtube.com
Matching graphs YouTube Define Matching Graph That is, each vertex in. Simply, there should not be any common vertex. A matching graph is a subgraph of a graph where there are no edges adjacent to each other. A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share a vertex in. A matching of. Define Matching Graph.
From studylib.net
Graph Matching Define Matching Graph A perfect matching in a graph g is a matching in which every vertex of g appears exactly once, that is, a matching of size exactly n=2. That is, each vertex in. A matching of graph g is a subgraph of g such that every edge shares no vertex with any other edge. A matching graph is a subgraph of. Define Matching Graph.
From www.youtube.com
Proof Regular Bipartite Graph has a Perfect Matching Graph Theory YouTube Define Matching Graph De nition 1 a matching m in a graph g(v;e) is a subset of the edge set e such that no two edges in m are incident on the same vertex, i.e. A matching graph is a subgraph of a graph where there are no edges adjacent to each other. That is, each vertex in. Simply, there should not be. Define Matching Graph.
From www.slideserve.com
PPT Graph pattern matching PowerPoint Presentation, free download ID2826667 Define Matching Graph De nition 1 a matching m in a graph g(v;e) is a subset of the edge set e such that no two edges in m are incident on the same vertex, i.e. A matching of graph g is a subgraph of g such that every edge shares no vertex with any other edge. A matching, also called an independent edge. Define Matching Graph.
From quizlet.com
Matching Graphs to Functions (MATH) Diagram Quizlet Define Matching Graph That is, each vertex in. A matching graph is a subgraph of a graph where there are no edges adjacent to each other. Simply, there should not be any common vertex. A matching of graph g is a subgraph of g such that every edge shares no vertex with any other edge. A matching, also called an independent edge set,. Define Matching Graph.
From www.slideserve.com
PPT Graph Matching PowerPoint Presentation, free download ID2306645 Define Matching Graph Simply, there should not be any common vertex. A matching of graph g is a subgraph of g such that every edge shares no vertex with any other edge. De nition 1 a matching m in a graph g(v;e) is a subset of the edge set e such that no two edges in m are incident on the same vertex,. Define Matching Graph.
From www.slideserve.com
PPT Exact (Graph) Matching PowerPoint Presentation, free download ID4094513 Define Matching Graph That is, each vertex in. De nition 1 a matching m in a graph g(v;e) is a subset of the edge set e such that no two edges in m are incident on the same vertex, i.e. Simply, there should not be any common vertex. A matching of graph g is a subgraph of g such that every edge shares. Define Matching Graph.
From www.researchgate.net
e An example of subgraph matching. The graph in Figure (a) is matched... Download Scientific Define Matching Graph De nition 1 a matching m in a graph g(v;e) is a subset of the edge set e such that no two edges in m are incident on the same vertex, i.e. That is, each vertex in. A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share. Define Matching Graph.
From issuu.com
Matching Graph by tutorcircle team Issuu Define Matching Graph A matching of graph g is a subgraph of g such that every edge shares no vertex with any other edge. A matching graph is a subgraph of a graph where there are no edges adjacent to each other. That is, each vertex in. Simply, there should not be any common vertex. De nition 1 a matching m in a. Define Matching Graph.
From www.youtube.com
Matching (graph theory) YouTube Define Matching Graph A matching graph is a subgraph of a graph where there are no edges adjacent to each other. A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share a vertex in. Simply, there should not be any common vertex. A perfect matching in a graph g is. Define Matching Graph.
From brilliant.org
Matching (Graph Theory) Brilliant Math & Science Wiki Define Matching Graph A matching of graph g is a subgraph of g such that every edge shares no vertex with any other edge. A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share a vertex in. That is, each vertex in. Simply, there should not be any common vertex.. Define Matching Graph.
From www.slideserve.com
PPT Discrete Mathematics Tutorial 13 PowerPoint Presentation, free download ID3073522 Define Matching Graph A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share a vertex in. A matching graph is a subgraph of a graph where there are no edges adjacent to each other. That is, each vertex in. A matching of graph g is a subgraph of g such. Define Matching Graph.
From www.geeksforgeeks.org
Mathematics Graph Theory Basics Set 1 Define Matching Graph A matching graph is a subgraph of a graph where there are no edges adjacent to each other. Simply, there should not be any common vertex. A matching of graph g is a subgraph of g such that every edge shares no vertex with any other edge. De nition 1 a matching m in a graph g(v;e) is a subset. Define Matching Graph.
From www.youtube.com
Graph Theory Matching definition YouTube Define Matching Graph A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share a vertex in. A matching graph is a subgraph of a graph where there are no edges adjacent to each other. A perfect matching in a graph g is a matching in which every vertex of g. Define Matching Graph.
From www.youtube.com
Matching in Graph Theory YouTube Define Matching Graph De nition 1 a matching m in a graph g(v;e) is a subset of the edge set e such that no two edges in m are incident on the same vertex, i.e. A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share a vertex in. A perfect. Define Matching Graph.
From www.youtube.com
Match the Equation with the Graph YouTube Define Matching Graph A matching graph is a subgraph of a graph where there are no edges adjacent to each other. A perfect matching in a graph g is a matching in which every vertex of g appears exactly once, that is, a matching of size exactly n=2. A matching of graph g is a subgraph of g such that every edge shares. Define Matching Graph.
From www.slideserve.com
PPT Label Placement and graph drawing PowerPoint Presentation, free download ID3293064 Define Matching Graph That is, each vertex in. A matching of graph g is a subgraph of g such that every edge shares no vertex with any other edge. Simply, there should not be any common vertex. A perfect matching in a graph g is a matching in which every vertex of g appears exactly once, that is, a matching of size exactly. Define Matching Graph.
From www.slideserve.com
PPT Matching graphs PowerPoint Presentation, free download ID887254 Define Matching Graph A matching graph is a subgraph of a graph where there are no edges adjacent to each other. Simply, there should not be any common vertex. A perfect matching in a graph g is a matching in which every vertex of g appears exactly once, that is, a matching of size exactly n=2. That is, each vertex in. A matching. Define Matching Graph.
From www.slideserve.com
PPT Matching in bipartite graphs PowerPoint Presentation, free download ID1448942 Define Matching Graph A perfect matching in a graph g is a matching in which every vertex of g appears exactly once, that is, a matching of size exactly n=2. A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share a vertex in. A matching graph is a subgraph of. Define Matching Graph.
From www.youtube.com
Matching Histograms with Box Plots YouTube Define Matching Graph De nition 1 a matching m in a graph g(v;e) is a subset of the edge set e such that no two edges in m are incident on the same vertex, i.e. A perfect matching in a graph g is a matching in which every vertex of g appears exactly once, that is, a matching of size exactly n=2. Simply,. Define Matching Graph.
From www.slideserve.com
PPT Graph Theory PowerPoint Presentation, free download ID2076639 Define Matching Graph A perfect matching in a graph g is a matching in which every vertex of g appears exactly once, that is, a matching of size exactly n=2. A matching graph is a subgraph of a graph where there are no edges adjacent to each other. A matching of graph g is a subgraph of g such that every edge shares. Define Matching Graph.
From bdpedigo.github.io
Graph matching — Network Data Science Define Matching Graph De nition 1 a matching m in a graph g(v;e) is a subset of the edge set e such that no two edges in m are incident on the same vertex, i.e. A matching graph is a subgraph of a graph where there are no edges adjacent to each other. A perfect matching in a graph g is a matching. Define Matching Graph.
From www.numerade.com
SOLVED Match the following graphs with their scaling of each set of axes and equations. Explain Define Matching Graph De nition 1 a matching m in a graph g(v;e) is a subset of the edge set e such that no two edges in m are incident on the same vertex, i.e. A matching, also called an independent edge set, on a graph is a set of edges of such that no two sets share a vertex in. A matching. Define Matching Graph.