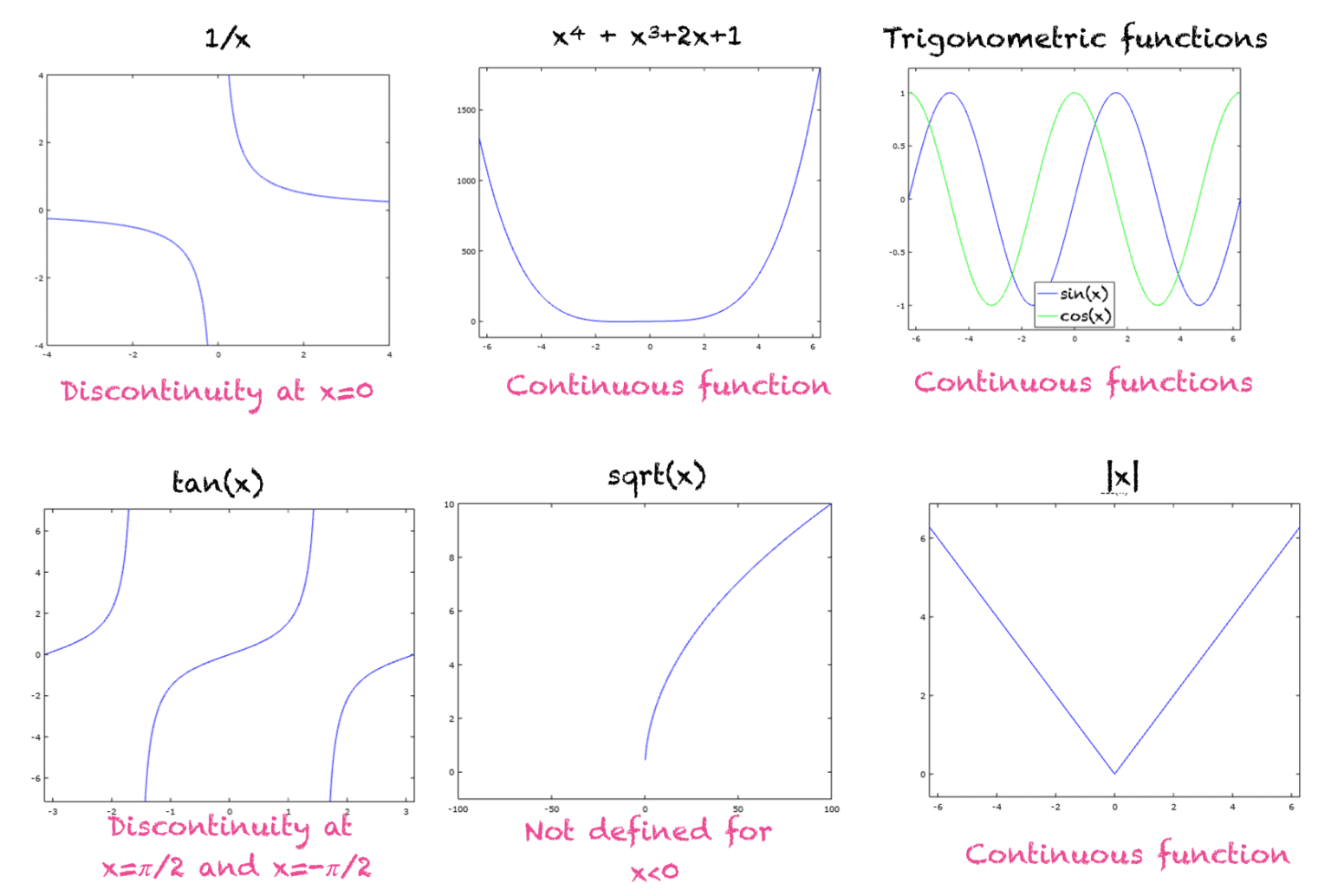
Continuous Linear Function . Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? $\map f x = \alpha x + \beta$ for all $x \in \r$. Since the functionals g and f coincide on y, \( [f]. Many of the results in calculus require that the functions be continuous, so having a strong understanding of continuous functions will be very important. The definition given by nctm in the common core mathematics companion. Prove that a linear functional $f:x \to \mathbb {r}$ is continuous if and only if there is a number $ c \in {0, \infty}$ such that $$|f (x)| \leq. In this section we introduce the idea of a continuous function. \r \to \r$ be a linear real function: We have from the definition of a linear functional: U[f] is a continuous linear functional given on the space y. Then $f$ is continuous at every real.
from machinelearningmastery.com
Many of the results in calculus require that the functions be continuous, so having a strong understanding of continuous functions will be very important. \r \to \r$ be a linear real function: Since the functionals g and f coincide on y, \( [f]. Then $f$ is continuous at every real. $\map f x = \alpha x + \beta$ for all $x \in \r$. U[f] is a continuous linear functional given on the space y. Prove that a linear functional $f:x \to \mathbb {r}$ is continuous if and only if there is a number $ c \in {0, \infty}$ such that $$|f (x)| \leq. In this section we introduce the idea of a continuous function. We have from the definition of a linear functional: Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)?
A Gentle Introduction to Continuous Functions
Continuous Linear Function Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? The definition given by nctm in the common core mathematics companion. U[f] is a continuous linear functional given on the space y. \r \to \r$ be a linear real function: Many of the results in calculus require that the functions be continuous, so having a strong understanding of continuous functions will be very important. Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? Since the functionals g and f coincide on y, \( [f]. We have from the definition of a linear functional: In this section we introduce the idea of a continuous function. Prove that a linear functional $f:x \to \mathbb {r}$ is continuous if and only if there is a number $ c \in {0, \infty}$ such that $$|f (x)| \leq. Then $f$ is continuous at every real. $\map f x = \alpha x + \beta$ for all $x \in \r$.
From www.slideserve.com
PPT 4.1 Intermediate Value Theorem for Continuous Functions Continuous Linear Function In this section we introduce the idea of a continuous function. \r \to \r$ be a linear real function: Then $f$ is continuous at every real. The definition given by nctm in the common core mathematics companion. Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? Many of the results in calculus require that. Continuous Linear Function.
From myah-bogspotbarajas.blogspot.com
How to Tell if a Graph Is Discrete or Continuous Continuous Linear Function Many of the results in calculus require that the functions be continuous, so having a strong understanding of continuous functions will be very important. The definition given by nctm in the common core mathematics companion. We have from the definition of a linear functional: Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? Since. Continuous Linear Function.
From www.mashupmath.com
How to Graph a Function in 3 Easy Steps — Mashup Math Continuous Linear Function We have from the definition of a linear functional: Prove that a linear functional $f:x \to \mathbb {r}$ is continuous if and only if there is a number $ c \in {0, \infty}$ such that $$|f (x)| \leq. \r \to \r$ be a linear real function: Are linear functions always continuous, or can they be discrete (as in an arithmetic. Continuous Linear Function.
From calcworkshop.com
Limits And Continuity (How To w/ StepbyStep Examples!) Continuous Linear Function Many of the results in calculus require that the functions be continuous, so having a strong understanding of continuous functions will be very important. Since the functionals g and f coincide on y, \( [f]. U[f] is a continuous linear functional given on the space y. \r \to \r$ be a linear real function: The definition given by nctm in. Continuous Linear Function.
From brainly.com
The graph of the continuous function g, the derivative of the function Continuous Linear Function Since the functionals g and f coincide on y, \( [f]. Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? \r \to \r$ be a linear real function: $\map f x = \alpha x + \beta$ for all $x \in \r$. In this section we introduce the idea of a continuous function. U[f] is. Continuous Linear Function.
From www.toppr.com
Algebra of Continuous Functions Introduction, Rules, Videos & Examples Continuous Linear Function Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? Prove that a linear functional $f:x \to \mathbb {r}$ is continuous if and only if there is a number $ c \in {0, \infty}$ such that $$|f (x)| \leq. Since the functionals g and f coincide on y, \( [f]. $\map f x = \alpha. Continuous Linear Function.
From articles.outlier.org
Continuous Functions Definition, Examples, and Properties Outlier Continuous Linear Function Many of the results in calculus require that the functions be continuous, so having a strong understanding of continuous functions will be very important. The definition given by nctm in the common core mathematics companion. \r \to \r$ be a linear real function: Then $f$ is continuous at every real. Since the functionals g and f coincide on y, \(. Continuous Linear Function.
From machinelearningmastery.com
A Gentle Introduction to Continuous Functions Continuous Linear Function \r \to \r$ be a linear real function: U[f] is a continuous linear functional given on the space y. $\map f x = \alpha x + \beta$ for all $x \in \r$. Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? In this section we introduce the idea of a continuous function. We have. Continuous Linear Function.
From kirbyaborted1970.blogspot.com
Can a Linear Function Be Continuous but Not Have a Domain and Range of Continuous Linear Function U[f] is a continuous linear functional given on the space y. Since the functionals g and f coincide on y, \( [f]. Many of the results in calculus require that the functions be continuous, so having a strong understanding of continuous functions will be very important. Prove that a linear functional $f:x \to \mathbb {r}$ is continuous if and only. Continuous Linear Function.
From www.youtube.com
Continuous and Uniformly Continuous Functions YouTube Continuous Linear Function Prove that a linear functional $f:x \to \mathbb {r}$ is continuous if and only if there is a number $ c \in {0, \infty}$ such that $$|f (x)| \leq. Many of the results in calculus require that the functions be continuous, so having a strong understanding of continuous functions will be very important. The definition given by nctm in the. Continuous Linear Function.
From www.youtube.com
Alg2T Ch1.1.2 One to One, Continuous, Linear Functions YouTube Continuous Linear Function We have from the definition of a linear functional: Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? In this section we introduce the idea of a continuous function. The definition given by nctm in the common core mathematics companion. Since the functionals g and f coincide on y, \( [f]. Then $f$ is. Continuous Linear Function.
From www.wikihow.com
How to Do Linear Functions 8 Steps (with Pictures) wikiHow Continuous Linear Function Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? U[f] is a continuous linear functional given on the space y. Since the functionals g and f coincide on y, \( [f]. \r \to \r$ be a linear real function: $\map f x = \alpha x + \beta$ for all $x \in \r$. In this. Continuous Linear Function.
From www.youtube.com
Finding the Slope of a Linear Function YouTube Continuous Linear Function We have from the definition of a linear functional: Many of the results in calculus require that the functions be continuous, so having a strong understanding of continuous functions will be very important. \r \to \r$ be a linear real function: Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? $\map f x =. Continuous Linear Function.
From www.cuemath.com
Continuous Function Definition, Examples Continuity Continuous Linear Function In this section we introduce the idea of a continuous function. U[f] is a continuous linear functional given on the space y. Then $f$ is continuous at every real. Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? The definition given by nctm in the common core mathematics companion. Since the functionals g and. Continuous Linear Function.
From lasmatesfaciles.com
How to Graph Linear Functions Quickly Mates Fáciles Continuous Linear Function Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? Since the functionals g and f coincide on y, \( [f]. U[f] is a continuous linear functional given on the space y. The definition given by nctm in the common core mathematics companion. $\map f x = \alpha x + \beta$ for all $x \in. Continuous Linear Function.
From www.shutterstock.com
Basic Properties Linear Functions On Coordinate Stock Vector (Royalty Continuous Linear Function Prove that a linear functional $f:x \to \mathbb {r}$ is continuous if and only if there is a number $ c \in {0, \infty}$ such that $$|f (x)| \leq. \r \to \r$ be a linear real function: Then $f$ is continuous at every real. Many of the results in calculus require that the functions be continuous, so having a strong. Continuous Linear Function.
From slideplayer.com
Linear Functions Ch.44 Recall what the word “linear” means… ppt download Continuous Linear Function We have from the definition of a linear functional: U[f] is a continuous linear functional given on the space y. \r \to \r$ be a linear real function: The definition given by nctm in the common core mathematics companion. In this section we introduce the idea of a continuous function. Prove that a linear functional $f:x \to \mathbb {r}$ is. Continuous Linear Function.
From granthamvanderch.blogspot.com
Example of Continuous Function That is Not Differentiable Grantham Continuous Linear Function Prove that a linear functional $f:x \to \mathbb {r}$ is continuous if and only if there is a number $ c \in {0, \infty}$ such that $$|f (x)| \leq. Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? U[f] is a continuous linear functional given on the space y. Many of the results in. Continuous Linear Function.
From www.expii.com
Graphing Linear Functions Expii Continuous Linear Function Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? $\map f x = \alpha x + \beta$ for all $x \in \r$. Then $f$ is continuous at every real. \r \to \r$ be a linear real function: We have from the definition of a linear functional: The definition given by nctm in the common. Continuous Linear Function.
From www.youtube.com
Discrete and Continuous Linear Functions YouTube Continuous Linear Function Since the functionals g and f coincide on y, \( [f]. Then $f$ is continuous at every real. U[f] is a continuous linear functional given on the space y. $\map f x = \alpha x + \beta$ for all $x \in \r$. We have from the definition of a linear functional: In this section we introduce the idea of a. Continuous Linear Function.
From courses.lumenlearning.com
Graphing Linear Equations Beginning Algebra Continuous Linear Function Since the functionals g and f coincide on y, \( [f]. U[f] is a continuous linear functional given on the space y. Then $f$ is continuous at every real. In this section we introduce the idea of a continuous function. \r \to \r$ be a linear real function: Many of the results in calculus require that the functions be continuous,. Continuous Linear Function.
From www.youtube.com
The Transfer Function of a ContinuousTime Linear System YouTube Continuous Linear Function Prove that a linear functional $f:x \to \mathbb {r}$ is continuous if and only if there is a number $ c \in {0, \infty}$ such that $$|f (x)| \leq. Since the functionals g and f coincide on y, \( [f]. We have from the definition of a linear functional: U[f] is a continuous linear functional given on the space y.. Continuous Linear Function.
From www.gauthmath.com
Solved Which statement best describes the functions represented here Continuous Linear Function Prove that a linear functional $f:x \to \mathbb {r}$ is continuous if and only if there is a number $ c \in {0, \infty}$ such that $$|f (x)| \leq. Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? U[f] is a continuous linear functional given on the space y. $\map f x = \alpha. Continuous Linear Function.
From www.madebyteachers.com
Linear Functions Graphing Lines Given Yintercept and an Ordered Pair Continuous Linear Function Prove that a linear functional $f:x \to \mathbb {r}$ is continuous if and only if there is a number $ c \in {0, \infty}$ such that $$|f (x)| \leq. $\map f x = \alpha x + \beta$ for all $x \in \r$. \r \to \r$ be a linear real function: We have from the definition of a linear functional: Many. Continuous Linear Function.
From www.expii.com
Continuous Data Definition & Examples Expii Continuous Linear Function We have from the definition of a linear functional: $\map f x = \alpha x + \beta$ for all $x \in \r$. U[f] is a continuous linear functional given on the space y. Many of the results in calculus require that the functions be continuous, so having a strong understanding of continuous functions will be very important. Are linear functions. Continuous Linear Function.
From analystprep.com
Properties of Continuous Uniform Distribution AnalystPrep CFA® Exam Continuous Linear Function Prove that a linear functional $f:x \to \mathbb {r}$ is continuous if and only if there is a number $ c \in {0, \infty}$ such that $$|f (x)| \leq. U[f] is a continuous linear functional given on the space y. We have from the definition of a linear functional: Many of the results in calculus require that the functions be. Continuous Linear Function.
From calcworkshop.com
Linear Combination of Random Variables (w/ 9 Examples!) Continuous Linear Function Prove that a linear functional $f:x \to \mathbb {r}$ is continuous if and only if there is a number $ c \in {0, \infty}$ such that $$|f (x)| \leq. $\map f x = \alpha x + \beta$ for all $x \in \r$. We have from the definition of a linear functional: In this section we introduce the idea of a. Continuous Linear Function.
From www.researchgate.net
6 A continuous piecewise linear function in V h . Download Continuous Linear Function $\map f x = \alpha x + \beta$ for all $x \in \r$. Then $f$ is continuous at every real. Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? \r \to \r$ be a linear real function: In this section we introduce the idea of a continuous function. Many of the results in calculus. Continuous Linear Function.
From www.ncl.ac.uk
Numeracy, Maths and Statistics Academic Skills Kit Continuous Linear Function \r \to \r$ be a linear real function: Then $f$ is continuous at every real. Many of the results in calculus require that the functions be continuous, so having a strong understanding of continuous functions will be very important. The definition given by nctm in the common core mathematics companion. In this section we introduce the idea of a continuous. Continuous Linear Function.
From betterlesson.com
Ninth grade Lesson Discrete and Continuous Functions Continuous Linear Function In this section we introduce the idea of a continuous function. U[f] is a continuous linear functional given on the space y. Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? $\map f x = \alpha x + \beta$ for all $x \in \r$. Then $f$ is continuous at every real. \r \to \r$. Continuous Linear Function.
From www.aplustopper.com
Continuous Function A Plus Topper Continuous Linear Function Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)? $\map f x = \alpha x + \beta$ for all $x \in \r$. We have from the definition of a linear functional: Many of the results in calculus require that the functions be continuous, so having a strong understanding of continuous functions will be very. Continuous Linear Function.
From www.slideserve.com
PPT Discrete and Continuous Functions PowerPoint Presentation, free Continuous Linear Function U[f] is a continuous linear functional given on the space y. Many of the results in calculus require that the functions be continuous, so having a strong understanding of continuous functions will be very important. \r \to \r$ be a linear real function: Since the functionals g and f coincide on y, \( [f]. Are linear functions always continuous, or. Continuous Linear Function.
From kirbyaborted1970.blogspot.com
Can a Linear Function Be Continuous but Not Have a Domain and Range of Continuous Linear Function In this section we introduce the idea of a continuous function. Then $f$ is continuous at every real. U[f] is a continuous linear functional given on the space y. Many of the results in calculus require that the functions be continuous, so having a strong understanding of continuous functions will be very important. We have from the definition of a. Continuous Linear Function.
From www.youtube.com
L11.3 A Linear Function of a Continuous Random Variable YouTube Continuous Linear Function U[f] is a continuous linear functional given on the space y. The definition given by nctm in the common core mathematics companion. We have from the definition of a linear functional: Many of the results in calculus require that the functions be continuous, so having a strong understanding of continuous functions will be very important. \r \to \r$ be a. Continuous Linear Function.
From www.cuemath.com
Continuous Function Definition, Examples Continuity Continuous Linear Function Prove that a linear functional $f:x \to \mathbb {r}$ is continuous if and only if there is a number $ c \in {0, \infty}$ such that $$|f (x)| \leq. Many of the results in calculus require that the functions be continuous, so having a strong understanding of continuous functions will be very important. Then $f$ is continuous at every real.. Continuous Linear Function.