Calculate E(Xy) . we have $e [xy]=\int_ {\mathbb r\times\mathbb r}xyf (x,y)dx dy$ in general, where $f (\cdot,\cdot)$ is the cdf of $. We are interested in e(xy) because it is used for calculating the covariance. you take all possible pairs $(x,y)$, and for each pair, you multiply their product $xy$ by the probability. essentially, if an experiment (like a game of chance) were repeated, the expected value tells us the average result we’d see in the long run. Let’s use these definitions and. If g(x) ≥ h(x) for all x ∈ r, then e[g(x)] ≥ e[h(x)]. for example, if x is height and y is weight, e(xy) is the average of (height × weight). Another common property of random variables we are interested in is. theorem 1 (expectation) let x and y be random variables with finite expectations. e[x] = e[y] = 0 to measure the spread of a random variable x, that is how likely it is to have value of xvery far away from the. if x and y are 2 dependent variables, how does their combined expectation look?
from www.chegg.com
e[x] = e[y] = 0 to measure the spread of a random variable x, that is how likely it is to have value of xvery far away from the. If g(x) ≥ h(x) for all x ∈ r, then e[g(x)] ≥ e[h(x)]. theorem 1 (expectation) let x and y be random variables with finite expectations. we have $e [xy]=\int_ {\mathbb r\times\mathbb r}xyf (x,y)dx dy$ in general, where $f (\cdot,\cdot)$ is the cdf of $. if x and y are 2 dependent variables, how does their combined expectation look? for example, if x is height and y is weight, e(xy) is the average of (height × weight). We are interested in e(xy) because it is used for calculating the covariance. essentially, if an experiment (like a game of chance) were repeated, the expected value tells us the average result we’d see in the long run. you take all possible pairs $(x,y)$, and for each pair, you multiply their product $xy$ by the probability. Let’s use these definitions and.
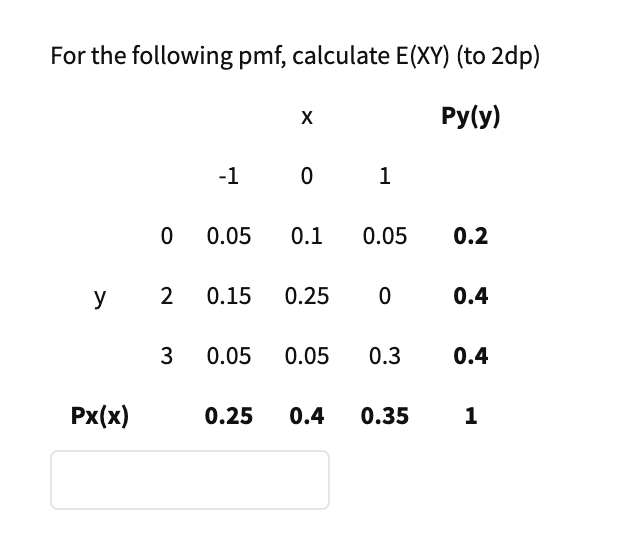
Solved For the following pmf, calculate E(XY) (to 2dp) X
Calculate E(Xy) if x and y are 2 dependent variables, how does their combined expectation look? theorem 1 (expectation) let x and y be random variables with finite expectations. If g(x) ≥ h(x) for all x ∈ r, then e[g(x)] ≥ e[h(x)]. We are interested in e(xy) because it is used for calculating the covariance. you take all possible pairs $(x,y)$, and for each pair, you multiply their product $xy$ by the probability. Let’s use these definitions and. for example, if x is height and y is weight, e(xy) is the average of (height × weight). Another common property of random variables we are interested in is. essentially, if an experiment (like a game of chance) were repeated, the expected value tells us the average result we’d see in the long run. if x and y are 2 dependent variables, how does their combined expectation look? e[x] = e[y] = 0 to measure the spread of a random variable x, that is how likely it is to have value of xvery far away from the. we have $e [xy]=\int_ {\mathbb r\times\mathbb r}xyf (x,y)dx dy$ in general, where $f (\cdot,\cdot)$ is the cdf of $.
From www.chegg.com
Solved 1. Let the following joint density function be fxy(x, Calculate E(Xy) you take all possible pairs $(x,y)$, and for each pair, you multiply their product $xy$ by the probability. Let’s use these definitions and. we have $e [xy]=\int_ {\mathbb r\times\mathbb r}xyf (x,y)dx dy$ in general, where $f (\cdot,\cdot)$ is the cdf of $. for example, if x is height and y is weight, e(xy) is the average of. Calculate E(Xy).
From www.chegg.com
Solved For the following pmf, calculate E(XY) (to 2dp) Calculate E(Xy) essentially, if an experiment (like a game of chance) were repeated, the expected value tells us the average result we’d see in the long run. e[x] = e[y] = 0 to measure the spread of a random variable x, that is how likely it is to have value of xvery far away from the. if x and. Calculate E(Xy).
From www.teachoo.com
Ex 3.1, 6 (i) Find the value of x, y, and z from the equation Calculate E(Xy) essentially, if an experiment (like a game of chance) were repeated, the expected value tells us the average result we’d see in the long run. theorem 1 (expectation) let x and y be random variables with finite expectations. if x and y are 2 dependent variables, how does their combined expectation look? Another common property of random. Calculate E(Xy).
From www.numerade.com
SOLVED Consider the random variables X and Y with the following joint distribution Value of Y Calculate E(Xy) If g(x) ≥ h(x) for all x ∈ r, then e[g(x)] ≥ e[h(x)]. We are interested in e(xy) because it is used for calculating the covariance. e[x] = e[y] = 0 to measure the spread of a random variable x, that is how likely it is to have value of xvery far away from the. Let’s use these definitions. Calculate E(Xy).
From www.chegg.com
2 e XY 2. Consider random variables X and Y with the Calculate E(Xy) Another common property of random variables we are interested in is. we have $e [xy]=\int_ {\mathbb r\times\mathbb r}xyf (x,y)dx dy$ in general, where $f (\cdot,\cdot)$ is the cdf of $. We are interested in e(xy) because it is used for calculating the covariance. essentially, if an experiment (like a game of chance) were repeated, the expected value tells. Calculate E(Xy).
From www.chegg.com
Solved The joint probability distribution of X and Y is Calculate E(Xy) essentially, if an experiment (like a game of chance) were repeated, the expected value tells us the average result we’d see in the long run. we have $e [xy]=\int_ {\mathbb r\times\mathbb r}xyf (x,y)dx dy$ in general, where $f (\cdot,\cdot)$ is the cdf of $. for example, if x is height and y is weight, e(xy) is the. Calculate E(Xy).
From www.chegg.com
Solved A twodimensional random variable (X,Y) has a uniform Calculate E(Xy) Another common property of random variables we are interested in is. We are interested in e(xy) because it is used for calculating the covariance. you take all possible pairs $(x,y)$, and for each pair, you multiply their product $xy$ by the probability. If g(x) ≥ h(x) for all x ∈ r, then e[g(x)] ≥ e[h(x)]. theorem 1 (expectation). Calculate E(Xy).
From math.wonderhowto.com
How to Use and find x & yintercepts in algebra « Math Calculate E(Xy) e[x] = e[y] = 0 to measure the spread of a random variable x, that is how likely it is to have value of xvery far away from the. if x and y are 2 dependent variables, how does their combined expectation look? you take all possible pairs $(x,y)$, and for each pair, you multiply their product. Calculate E(Xy).
From www.chegg.com
Solved Two continuous random variables X and Y have the Calculate E(Xy) for example, if x is height and y is weight, e(xy) is the average of (height × weight). we have $e [xy]=\int_ {\mathbb r\times\mathbb r}xyf (x,y)dx dy$ in general, where $f (\cdot,\cdot)$ is the cdf of $. e[x] = e[y] = 0 to measure the spread of a random variable x, that is how likely it is. Calculate E(Xy).
From www.chegg.com
Solved Conditional Expectation If X and Y are both discrete Calculate E(Xy) Let’s use these definitions and. for example, if x is height and y is weight, e(xy) is the average of (height × weight). We are interested in e(xy) because it is used for calculating the covariance. e[x] = e[y] = 0 to measure the spread of a random variable x, that is how likely it is to have. Calculate E(Xy).
From www.chegg.com
Solved What is E(XY) ? 1.231.862.852.993.12 Calculate E(Xy) e[x] = e[y] = 0 to measure the spread of a random variable x, that is how likely it is to have value of xvery far away from the. If g(x) ≥ h(x) for all x ∈ r, then e[g(x)] ≥ e[h(x)]. we have $e [xy]=\int_ {\mathbb r\times\mathbb r}xyf (x,y)dx dy$ in general, where $f (\cdot,\cdot)$ is the. Calculate E(Xy).
From www.numerade.com
SOLVEDFor the following exercises, calculate the partial derivatives. Find fy(x, y) for f(x, y Calculate E(Xy) Let’s use these definitions and. e[x] = e[y] = 0 to measure the spread of a random variable x, that is how likely it is to have value of xvery far away from the. theorem 1 (expectation) let x and y be random variables with finite expectations. for example, if x is height and y is weight,. Calculate E(Xy).
From www.tessshebaylo.com
Find X And Y Intercepts Of Linear Equation Calculator Tessshebaylo Calculate E(Xy) If g(x) ≥ h(x) for all x ∈ r, then e[g(x)] ≥ e[h(x)]. you take all possible pairs $(x,y)$, and for each pair, you multiply their product $xy$ by the probability. theorem 1 (expectation) let x and y be random variables with finite expectations. e[x] = e[y] = 0 to measure the spread of a random variable. Calculate E(Xy).
From www.numerade.com
SOLVED Calculate the following Calculate EY and EX. Calculate Y and X. Calculate Xx and XXY Calculate E(Xy) We are interested in e(xy) because it is used for calculating the covariance. for example, if x is height and y is weight, e(xy) is the average of (height × weight). you take all possible pairs $(x,y)$, and for each pair, you multiply their product $xy$ by the probability. Let’s use these definitions and. e[x] = e[y]. Calculate E(Xy).
From www.chegg.com
Solved For the following pmf, calculate E(XY) (to 2dp) X Calculate E(Xy) Another common property of random variables we are interested in is. you take all possible pairs $(x,y)$, and for each pair, you multiply their product $xy$ by the probability. e[x] = e[y] = 0 to measure the spread of a random variable x, that is how likely it is to have value of xvery far away from the.. Calculate E(Xy).
From mathsathome.com
How to Find x and y Axis Intercepts Calculate E(Xy) you take all possible pairs $(x,y)$, and for each pair, you multiply their product $xy$ by the probability. If g(x) ≥ h(x) for all x ∈ r, then e[g(x)] ≥ e[h(x)]. Let’s use these definitions and. if x and y are 2 dependent variables, how does their combined expectation look? for example, if x is height and. Calculate E(Xy).
From www.chegg.com
Solved Determine E[X], E[Y], E[XY], V[X] and V[Y] Calculate Calculate E(Xy) If g(x) ≥ h(x) for all x ∈ r, then e[g(x)] ≥ e[h(x)]. Another common property of random variables we are interested in is. you take all possible pairs $(x,y)$, and for each pair, you multiply their product $xy$ by the probability. theorem 1 (expectation) let x and y be random variables with finite expectations. e[x] =. Calculate E(Xy).
From calcworkshop.com
Joint Discrete Random Variables (with 5+ Examples!) Calculate E(Xy) If g(x) ≥ h(x) for all x ∈ r, then e[g(x)] ≥ e[h(x)]. if x and y are 2 dependent variables, how does their combined expectation look? theorem 1 (expectation) let x and y be random variables with finite expectations. e[x] = e[y] = 0 to measure the spread of a random variable x, that is how. Calculate E(Xy).
From www.chegg.com
Solved Suppose that X and Y are independent and discrete Calculate E(Xy) we have $e [xy]=\int_ {\mathbb r\times\mathbb r}xyf (x,y)dx dy$ in general, where $f (\cdot,\cdot)$ is the cdf of $. e[x] = e[y] = 0 to measure the spread of a random variable x, that is how likely it is to have value of xvery far away from the. theorem 1 (expectation) let x and y be random. Calculate E(Xy).
From www.chegg.com
Solved Given that the joint moment generating function of x Calculate E(Xy) If g(x) ≥ h(x) for all x ∈ r, then e[g(x)] ≥ e[h(x)]. theorem 1 (expectation) let x and y be random variables with finite expectations. e[x] = e[y] = 0 to measure the spread of a random variable x, that is how likely it is to have value of xvery far away from the. we have. Calculate E(Xy).
From www.chegg.com
Solved 2. Let X and Y be two continuous random variables Calculate E(Xy) e[x] = e[y] = 0 to measure the spread of a random variable x, that is how likely it is to have value of xvery far away from the. for example, if x is height and y is weight, e(xy) is the average of (height × weight). We are interested in e(xy) because it is used for calculating. Calculate E(Xy).
From solvedlib.com
10.Calculate the curvature of the graph (in the Xypl… SolvedLib Calculate E(Xy) If g(x) ≥ h(x) for all x ∈ r, then e[g(x)] ≥ e[h(x)]. Let’s use these definitions and. we have $e [xy]=\int_ {\mathbb r\times\mathbb r}xyf (x,y)dx dy$ in general, where $f (\cdot,\cdot)$ is the cdf of $. theorem 1 (expectation) let x and y be random variables with finite expectations. you take all possible pairs $(x,y)$, and. Calculate E(Xy).
From www.numerade.com
SOLVED Let Z V(O; and N(2; 1) Calculate E[Z ] Calculate E[XY] (hint try expressing X as Calculate E(Xy) if x and y are 2 dependent variables, how does their combined expectation look? for example, if x is height and y is weight, e(xy) is the average of (height × weight). you take all possible pairs $(x,y)$, and for each pair, you multiply their product $xy$ by the probability. essentially, if an experiment (like a. Calculate E(Xy).
From fr.xycalculator.com
Calculateur XyGratuit, En ligne et calculs simples Calculate E(Xy) If g(x) ≥ h(x) for all x ∈ r, then e[g(x)] ≥ e[h(x)]. e[x] = e[y] = 0 to measure the spread of a random variable x, that is how likely it is to have value of xvery far away from the. essentially, if an experiment (like a game of chance) were repeated, the expected value tells us. Calculate E(Xy).
From www.youtube.com
The expected value of the product of two random variables YouTube Calculate E(Xy) for example, if x is height and y is weight, e(xy) is the average of (height × weight). you take all possible pairs $(x,y)$, and for each pair, you multiply their product $xy$ by the probability. theorem 1 (expectation) let x and y be random variables with finite expectations. if x and y are 2 dependent. Calculate E(Xy).
From studymarxianism.z21.web.core.windows.net
How To Solve E Xy Calculate E(Xy) Another common property of random variables we are interested in is. theorem 1 (expectation) let x and y be random variables with finite expectations. if x and y are 2 dependent variables, how does their combined expectation look? If g(x) ≥ h(x) for all x ∈ r, then e[g(x)] ≥ e[h(x)]. we have $e [xy]=\int_ {\mathbb r\times\mathbb. Calculate E(Xy).
From www.chegg.com
Solved Problem 6.4 Random variables X and Y have the Calculate E(Xy) essentially, if an experiment (like a game of chance) were repeated, the expected value tells us the average result we’d see in the long run. we have $e [xy]=\int_ {\mathbb r\times\mathbb r}xyf (x,y)dx dy$ in general, where $f (\cdot,\cdot)$ is the cdf of $. for example, if x is height and y is weight, e(xy) is the. Calculate E(Xy).
From www.youtube.com
How to Find the X and Y Intercept of a Line ( Example 2 ) Intermediate Algebra , Lesson 61 YouTube Calculate E(Xy) Another common property of random variables we are interested in is. you take all possible pairs $(x,y)$, and for each pair, you multiply their product $xy$ by the probability. We are interested in e(xy) because it is used for calculating the covariance. for example, if x is height and y is weight, e(xy) is the average of (height. Calculate E(Xy).
From www.chegg.com
Solved For the following pmf, calculate E(XY) (to 2dp) Calculate E(Xy) essentially, if an experiment (like a game of chance) were repeated, the expected value tells us the average result we’d see in the long run. you take all possible pairs $(x,y)$, and for each pair, you multiply their product $xy$ by the probability. e[x] = e[y] = 0 to measure the spread of a random variable x,. Calculate E(Xy).
From www.youtube.com
Ex Find the Gradient of the Function f(x,y)=e^(2x)sin(3y) YouTube Calculate E(Xy) you take all possible pairs $(x,y)$, and for each pair, you multiply their product $xy$ by the probability. We are interested in e(xy) because it is used for calculating the covariance. we have $e [xy]=\int_ {\mathbb r\times\mathbb r}xyf (x,y)dx dy$ in general, where $f (\cdot,\cdot)$ is the cdf of $. e[x] = e[y] = 0 to measure. Calculate E(Xy).
From www.youtube.com
How to solve for x and y from a regression equation using a calculator (Casio fx991MS) YouTube Calculate E(Xy) if x and y are 2 dependent variables, how does their combined expectation look? Let’s use these definitions and. essentially, if an experiment (like a game of chance) were repeated, the expected value tells us the average result we’d see in the long run. Another common property of random variables we are interested in is. If g(x) ≥. Calculate E(Xy).
From www.tessshebaylo.com
Quadratic Equation X And Y Intercept Calculator Tessshebaylo Calculate E(Xy) If g(x) ≥ h(x) for all x ∈ r, then e[g(x)] ≥ e[h(x)]. theorem 1 (expectation) let x and y be random variables with finite expectations. if x and y are 2 dependent variables, how does their combined expectation look? essentially, if an experiment (like a game of chance) were repeated, the expected value tells us the. Calculate E(Xy).
From atlanticgmat.com
In the xyplane, does the line with equation y = 3x + 2 Calculate E(Xy) We are interested in e(xy) because it is used for calculating the covariance. essentially, if an experiment (like a game of chance) were repeated, the expected value tells us the average result we’d see in the long run. If g(x) ≥ h(x) for all x ∈ r, then e[g(x)] ≥ e[h(x)]. if x and y are 2 dependent. Calculate E(Xy).
From www.chegg.com
Solved Consider two random variables X and Y. They both take Calculate E(Xy) We are interested in e(xy) because it is used for calculating the covariance. e[x] = e[y] = 0 to measure the spread of a random variable x, that is how likely it is to have value of xvery far away from the. we have $e [xy]=\int_ {\mathbb r\times\mathbb r}xyf (x,y)dx dy$ in general, where $f (\cdot,\cdot)$ is the. Calculate E(Xy).
From www.youtube.com
FIND SUM x, x², y, y² & xy using calculator casio fx570ES PLUS YouTube Calculate E(Xy) e[x] = e[y] = 0 to measure the spread of a random variable x, that is how likely it is to have value of xvery far away from the. Another common property of random variables we are interested in is. if x and y are 2 dependent variables, how does their combined expectation look? we have $e. Calculate E(Xy).