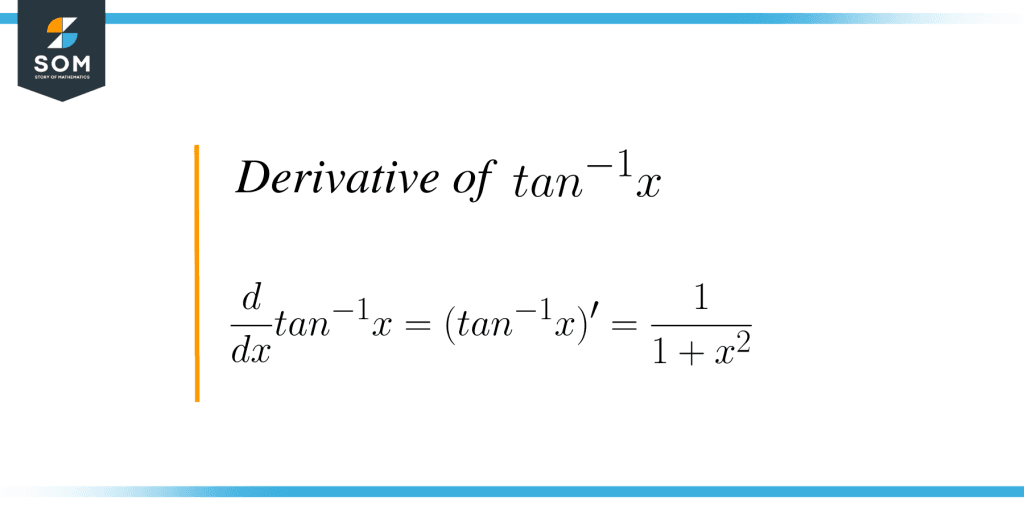Differentiation Formula Tan Inverse . The function \ (g (x)=\sqrt [3] {x}\) is the inverse of. Use the inverse function theorem to find the derivative of \ (g (x)=\sqrt [3] {x}\). \[\sec y\tan y \cdot \frac{dy}{dx} = 1\] solving this for. Find the derivative of \(f(x)=\tan^{−1}(x^2).\) Differentiation of tan inverse x is the process of evaluating the derivative of tan inverse x with respect to x which is given by 1/ (1 + x 2). The derivatives of the remaining inverse. Applying differentiation formulas to an inverse tangent function. Use the inverse function theorem to find the derivative of g (x) = tan −1 x. To differentiate it quickly, we have two options: G (x) = tan −1 x. Y = tan −1 x =. Let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent function: In this article, we will learn about the derivative of tan inverse x and its formula including the proof of the formula using the first. Differentiating equation \ref{inverseeqsec} implicitly with respect to \(x\), gives us:
from www.storyofmathematics.com
The derivatives of the remaining inverse. Find the derivative of \(f(x)=\tan^{−1}(x^2).\) In this article, we will learn about the derivative of tan inverse x and its formula including the proof of the formula using the first. Differentiating equation \ref{inverseeqsec} implicitly with respect to \(x\), gives us: The function \ (g (x)=\sqrt [3] {x}\) is the inverse of. Let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent function: Differentiation of tan inverse x is the process of evaluating the derivative of tan inverse x with respect to x which is given by 1/ (1 + x 2). Y = tan −1 x =. \[\sec y\tan y \cdot \frac{dy}{dx} = 1\] solving this for. Use the inverse function theorem to find the derivative of g (x) = tan −1 x.
Derivative of Tan^1 x Detailed Explanation and Examples The Story
Differentiation Formula Tan Inverse \[\sec y\tan y \cdot \frac{dy}{dx} = 1\] solving this for. The derivatives of the remaining inverse. Y = tan −1 x =. Differentiating equation \ref{inverseeqsec} implicitly with respect to \(x\), gives us: The function \ (g (x)=\sqrt [3] {x}\) is the inverse of. G (x) = tan −1 x. Use the inverse function theorem to find the derivative of g (x) = tan −1 x. Find the derivative of \(f(x)=\tan^{−1}(x^2).\) Let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent function: Applying differentiation formulas to an inverse tangent function. In this article, we will learn about the derivative of tan inverse x and its formula including the proof of the formula using the first. To differentiate it quickly, we have two options: Differentiation of tan inverse x is the process of evaluating the derivative of tan inverse x with respect to x which is given by 1/ (1 + x 2). Use the inverse function theorem to find the derivative of \ (g (x)=\sqrt [3] {x}\). \[\sec y\tan y \cdot \frac{dy}{dx} = 1\] solving this for.
From www.youtube.com
Derivatives of Inverse Trigonometric Functions YouTube Differentiation Formula Tan Inverse Y = tan −1 x =. Applying differentiation formulas to an inverse tangent function. Differentiating equation \ref{inverseeqsec} implicitly with respect to \(x\), gives us: The derivatives of the remaining inverse. Differentiation of tan inverse x is the process of evaluating the derivative of tan inverse x with respect to x which is given by 1/ (1 + x 2). Use. Differentiation Formula Tan Inverse.
From www.adda247.com
Differentiation of Tan Inverse x Explanation, Formula, Examples Differentiation Formula Tan Inverse \[\sec y\tan y \cdot \frac{dy}{dx} = 1\] solving this for. G (x) = tan −1 x. The function \ (g (x)=\sqrt [3] {x}\) is the inverse of. The derivatives of the remaining inverse. Y = tan −1 x =. Find the derivative of \(f(x)=\tan^{−1}(x^2).\) Use the inverse function theorem to find the derivative of g (x) = tan −1 x.. Differentiation Formula Tan Inverse.
From materialfullvalorous.z13.web.core.windows.net
Inverse Trigonometry Formula Sheet Differentiation Formula Tan Inverse Find the derivative of \(f(x)=\tan^{−1}(x^2).\) Applying differentiation formulas to an inverse tangent function. \[\sec y\tan y \cdot \frac{dy}{dx} = 1\] solving this for. The derivatives of the remaining inverse. Let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent function: In this article, we will learn about the. Differentiation Formula Tan Inverse.
From www.youtube.com
Derivative of Inverse Tangent Function or y=arctanx YouTube Differentiation Formula Tan Inverse G (x) = tan −1 x. Use the inverse function theorem to find the derivative of g (x) = tan −1 x. The function \ (g (x)=\sqrt [3] {x}\) is the inverse of. Y = tan −1 x =. Let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the. Differentiation Formula Tan Inverse.
From www.youtube.com
Derivative of the inverse tangent of the square root of x YouTube Differentiation Formula Tan Inverse In this article, we will learn about the derivative of tan inverse x and its formula including the proof of the formula using the first. The function \ (g (x)=\sqrt [3] {x}\) is the inverse of. Differentiation of tan inverse x is the process of evaluating the derivative of tan inverse x with respect to x which is given by. Differentiation Formula Tan Inverse.
From study.com
Derivative of Tan Differentiation & Formula Lesson Differentiation Formula Tan Inverse Use the inverse function theorem to find the derivative of g (x) = tan −1 x. Differentiating equation \ref{inverseeqsec} implicitly with respect to \(x\), gives us: The function \ (g (x)=\sqrt [3] {x}\) is the inverse of. Use the inverse function theorem to find the derivative of \ (g (x)=\sqrt [3] {x}\). Differentiation of tan inverse x is the process. Differentiation Formula Tan Inverse.
From www.youtube.com
Derivative of tan^1(x/a) Differentiation of Inverse Trigonometric Differentiation Formula Tan Inverse Y = tan −1 x =. \[\sec y\tan y \cdot \frac{dy}{dx} = 1\] solving this for. Applying differentiation formulas to an inverse tangent function. Let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent function: G (x) = tan −1 x. Differentiating equation \ref{inverseeqsec} implicitly with respect to. Differentiation Formula Tan Inverse.
From www.nagwa.com
Question Video The Derivative of an Inverse Tangent Function Nagwa Differentiation Formula Tan Inverse Y = tan −1 x =. In this article, we will learn about the derivative of tan inverse x and its formula including the proof of the formula using the first. To differentiate it quickly, we have two options: Use the inverse function theorem to find the derivative of g (x) = tan −1 x. Use the inverse function theorem. Differentiation Formula Tan Inverse.
From geteducationbee.com
Derivative of tangent x, sec x & tan x Longer Free Tutorial Get Differentiation Formula Tan Inverse Use the inverse function theorem to find the derivative of \ (g (x)=\sqrt [3] {x}\). To differentiate it quickly, we have two options: Find the derivative of \(f(x)=\tan^{−1}(x^2).\) In this article, we will learn about the derivative of tan inverse x and its formula including the proof of the formula using the first. The derivatives of the remaining inverse. G. Differentiation Formula Tan Inverse.
From www.cuemath.com
Inverse Tan (Inverse Tangent) Formula, Graph Tan Inverse x Differentiation Formula Tan Inverse G (x) = tan −1 x. Find the derivative of \(f(x)=\tan^{−1}(x^2).\) \[\sec y\tan y \cdot \frac{dy}{dx} = 1\] solving this for. Differentiating equation \ref{inverseeqsec} implicitly with respect to \(x\), gives us: Applying differentiation formulas to an inverse tangent function. To differentiate it quickly, we have two options: In this article, we will learn about the derivative of tan inverse x. Differentiation Formula Tan Inverse.
From www.youtube.com
Derivative of inverse hyperbolic tan(x) Differentiation YouTube Differentiation Formula Tan Inverse To differentiate it quickly, we have two options: Applying differentiation formulas to an inverse tangent function. Differentiation of tan inverse x is the process of evaluating the derivative of tan inverse x with respect to x which is given by 1/ (1 + x 2). In this article, we will learn about the derivative of tan inverse x and its. Differentiation Formula Tan Inverse.
From www.youtube.com
Differentiating inverse tan(x/a) ExamSolutions Maths Revision YouTube Differentiation Formula Tan Inverse To differentiate it quickly, we have two options: Use the inverse function theorem to find the derivative of g (x) = tan −1 x. G (x) = tan −1 x. Applying differentiation formulas to an inverse tangent function. Use the inverse function theorem to find the derivative of \ (g (x)=\sqrt [3] {x}\). Let’s use our formula for the derivative. Differentiation Formula Tan Inverse.
From peakd.com
Derivative of Inverse Hyperbolic Trigonometry tanh^1(x) PeakD Differentiation Formula Tan Inverse In this article, we will learn about the derivative of tan inverse x and its formula including the proof of the formula using the first. Differentiation of tan inverse x is the process of evaluating the derivative of tan inverse x with respect to x which is given by 1/ (1 + x 2). The function \ (g (x)=\sqrt [3]. Differentiation Formula Tan Inverse.
From www.teachoo.com
Inverse Trigonometry Formulas with Examples Teachoo Formulae bas Differentiation Formula Tan Inverse Y = tan −1 x =. G (x) = tan −1 x. Use the inverse function theorem to find the derivative of \ (g (x)=\sqrt [3] {x}\). Find the derivative of \(f(x)=\tan^{−1}(x^2).\) To differentiate it quickly, we have two options: The derivatives of the remaining inverse. In this article, we will learn about the derivative of tan inverse x and. Differentiation Formula Tan Inverse.
From www.teachoo.com
Example 27 Find derivative of f(x) = tan1 x Class 12 Differentiation Formula Tan Inverse Applying differentiation formulas to an inverse tangent function. To differentiate it quickly, we have two options: \[\sec y\tan y \cdot \frac{dy}{dx} = 1\] solving this for. Use the inverse function theorem to find the derivative of \ (g (x)=\sqrt [3] {x}\). The function \ (g (x)=\sqrt [3] {x}\) is the inverse of. Y = tan −1 x =. G (x). Differentiation Formula Tan Inverse.
From www.youtube.com
Deriving the Derivative of Inverse Tangent or y = arctan (x) YouTube Differentiation Formula Tan Inverse The function \ (g (x)=\sqrt [3] {x}\) is the inverse of. G (x) = tan −1 x. Find the derivative of \(f(x)=\tan^{−1}(x^2).\) Use the inverse function theorem to find the derivative of g (x) = tan −1 x. In this article, we will learn about the derivative of tan inverse x and its formula including the proof of the formula. Differentiation Formula Tan Inverse.
From brainly.in
Differentiation of tan inverse x is ? Brainly.in Differentiation Formula Tan Inverse Differentiating equation \ref{inverseeqsec} implicitly with respect to \(x\), gives us: Differentiation of tan inverse x is the process of evaluating the derivative of tan inverse x with respect to x which is given by 1/ (1 + x 2). Use the inverse function theorem to find the derivative of \ (g (x)=\sqrt [3] {x}\). \[\sec y\tan y \cdot \frac{dy}{dx} =. Differentiation Formula Tan Inverse.
From www.slideserve.com
PPT 3.8 Derivatives of Inverse Trigonometric Functions PowerPoint Differentiation Formula Tan Inverse G (x) = tan −1 x. Let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent function: Use the inverse function theorem to find the derivative of \ (g (x)=\sqrt [3] {x}\). Applying differentiation formulas to an inverse tangent function. \[\sec y\tan y \cdot \frac{dy}{dx} = 1\] solving. Differentiation Formula Tan Inverse.
From www.adda247.com
Differentiation of Tan Inverse x Explanation, Formula, Examples Differentiation Formula Tan Inverse The derivatives of the remaining inverse. Y = tan −1 x =. Differentiating equation \ref{inverseeqsec} implicitly with respect to \(x\), gives us: To differentiate it quickly, we have two options: Differentiation of tan inverse x is the process of evaluating the derivative of tan inverse x with respect to x which is given by 1/ (1 + x 2). Use. Differentiation Formula Tan Inverse.
From www.teachoo.com
Differentiation Formulas & Rules Basic,Trig Full list Teachoo Differentiation Formula Tan Inverse The function \ (g (x)=\sqrt [3] {x}\) is the inverse of. In this article, we will learn about the derivative of tan inverse x and its formula including the proof of the formula using the first. Applying differentiation formulas to an inverse tangent function. Differentiation of tan inverse x is the process of evaluating the derivative of tan inverse x. Differentiation Formula Tan Inverse.
From www.youtube.com
Derivative of tan Inverse Differentiation of tan Inverse (Proof Differentiation Formula Tan Inverse To differentiate it quickly, we have two options: Let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent function: \[\sec y\tan y \cdot \frac{dy}{dx} = 1\] solving this for. Y = tan −1 x =. The derivatives of the remaining inverse. In this article, we will learn about. Differentiation Formula Tan Inverse.
From www.youtube.com
Differentiation of inverse tanh (tanh^1(x)) YouTube Differentiation Formula Tan Inverse The derivatives of the remaining inverse. G (x) = tan −1 x. Let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent function: Use the inverse function theorem to find the derivative of g (x) = tan −1 x. Find the derivative of \(f(x)=\tan^{−1}(x^2).\) Differentiation of tan inverse. Differentiation Formula Tan Inverse.
From www.adda247.com
Differentiation of Tan Inverse x Explanation, Formula, Examples Differentiation Formula Tan Inverse G (x) = tan −1 x. The function \ (g (x)=\sqrt [3] {x}\) is the inverse of. Let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent function: Use the inverse function theorem to find the derivative of g (x) = tan −1 x. To differentiate it quickly,. Differentiation Formula Tan Inverse.
From www.youtube.com
How to Find the Derivative of the Inverse Hyperbolic Sine of the Differentiation Formula Tan Inverse In this article, we will learn about the derivative of tan inverse x and its formula including the proof of the formula using the first. Differentiating equation \ref{inverseeqsec} implicitly with respect to \(x\), gives us: Applying differentiation formulas to an inverse tangent function. Y = tan −1 x =. Use the inverse function theorem to find the derivative of g. Differentiation Formula Tan Inverse.
From www.cuemath.com
Derivatives Calculus, Meaning, Interpretation Differentiation Formula Tan Inverse Use the inverse function theorem to find the derivative of \ (g (x)=\sqrt [3] {x}\). The function \ (g (x)=\sqrt [3] {x}\) is the inverse of. G (x) = tan −1 x. Let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent function: Use the inverse function theorem. Differentiation Formula Tan Inverse.
From www.teachoo.com
Inverse Trigonometry Formulas with Examples Teachoo Formulae bas Differentiation Formula Tan Inverse In this article, we will learn about the derivative of tan inverse x and its formula including the proof of the formula using the first. The derivatives of the remaining inverse. The function \ (g (x)=\sqrt [3] {x}\) is the inverse of. Use the inverse function theorem to find the derivative of g (x) = tan −1 x. Let’s use. Differentiation Formula Tan Inverse.
From www.youtube.com
Differentiation of inverse tan YouTube Differentiation Formula Tan Inverse Find the derivative of \(f(x)=\tan^{−1}(x^2).\) Y = tan −1 x =. Use the inverse function theorem to find the derivative of \ (g (x)=\sqrt [3] {x}\). Differentiating equation \ref{inverseeqsec} implicitly with respect to \(x\), gives us: The function \ (g (x)=\sqrt [3] {x}\) is the inverse of. Applying differentiation formulas to an inverse tangent function. Use the inverse function theorem. Differentiation Formula Tan Inverse.
From www.nagwa.com
Question Video The Derivative of an Inverse Tangent Function Nagwa Differentiation Formula Tan Inverse To differentiate it quickly, we have two options: \[\sec y\tan y \cdot \frac{dy}{dx} = 1\] solving this for. In this article, we will learn about the derivative of tan inverse x and its formula including the proof of the formula using the first. The function \ (g (x)=\sqrt [3] {x}\) is the inverse of. Find the derivative of \(f(x)=\tan^{−1}(x^2).\) Differentiating. Differentiation Formula Tan Inverse.
From www.storyofmathematics.com
Derivative of Tan^1 x Detailed Explanation and Examples The Story Differentiation Formula Tan Inverse Use the inverse function theorem to find the derivative of g (x) = tan −1 x. Differentiating equation \ref{inverseeqsec} implicitly with respect to \(x\), gives us: In this article, we will learn about the derivative of tan inverse x and its formula including the proof of the formula using the first. The derivatives of the remaining inverse. G (x) =. Differentiation Formula Tan Inverse.
From www.pinterest.es
Derivatives of inverse trig functions Mathematics education, Studying Differentiation Formula Tan Inverse Let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent function: To differentiate it quickly, we have two options: Differentiating equation \ref{inverseeqsec} implicitly with respect to \(x\), gives us: In this article, we will learn about the derivative of tan inverse x and its formula including the proof. Differentiation Formula Tan Inverse.
From www.teachoo.com
Example 27 Find derivative of f(x) = tan1 x Class 12 Differentiation Formula Tan Inverse To differentiate it quickly, we have two options: Applying differentiation formulas to an inverse tangent function. The derivatives of the remaining inverse. G (x) = tan −1 x. In this article, we will learn about the derivative of tan inverse x and its formula including the proof of the formula using the first. \[\sec y\tan y \cdot \frac{dy}{dx} = 1\]. Differentiation Formula Tan Inverse.
From www.youtube.com
Derivative of Inverse tan x by first principle method YouTube Differentiation Formula Tan Inverse To differentiate it quickly, we have two options: Find the derivative of \(f(x)=\tan^{−1}(x^2).\) Differentiating equation \ref{inverseeqsec} implicitly with respect to \(x\), gives us: G (x) = tan −1 x. Use the inverse function theorem to find the derivative of g (x) = tan −1 x. The function \ (g (x)=\sqrt [3] {x}\) is the inverse of. Use the inverse function. Differentiation Formula Tan Inverse.
From calcworkshop.com
Derivative Of Inverse Functions (How To w/ Examples!) Differentiation Formula Tan Inverse Let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent function: The derivatives of the remaining inverse. \[\sec y\tan y \cdot \frac{dy}{dx} = 1\] solving this for. Use the inverse function theorem to find the derivative of \ (g (x)=\sqrt [3] {x}\). Differentiating equation \ref{inverseeqsec} implicitly with respect. Differentiation Formula Tan Inverse.
From www.youtube.com
Derivative of tan inverse with chain rule YouTube Differentiation Formula Tan Inverse Applying differentiation formulas to an inverse tangent function. The derivatives of the remaining inverse. Let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent function: Find the derivative of \(f(x)=\tan^{−1}(x^2).\) Differentiation of tan inverse x is the process of evaluating the derivative of tan inverse x with respect. Differentiation Formula Tan Inverse.
From www.youtube.com
Derivative of Inverse Tangent (Arctan) with example YouTube Differentiation Formula Tan Inverse Differentiating equation \ref{inverseeqsec} implicitly with respect to \(x\), gives us: The derivatives of the remaining inverse. To differentiate it quickly, we have two options: In this article, we will learn about the derivative of tan inverse x and its formula including the proof of the formula using the first. Applying differentiation formulas to an inverse tangent function. G (x) =. Differentiation Formula Tan Inverse.