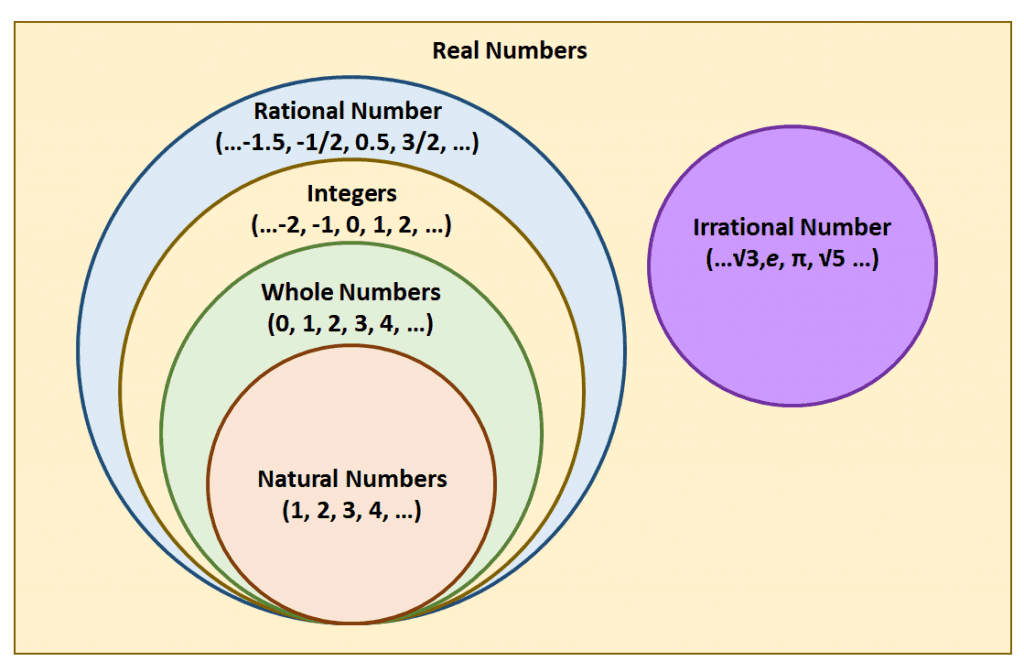
Closed Under Meaning . Closure property states that when a set of numbers is closed under any arithmetic operation such as addition, subtraction, multiplication, and division, it means that when the operation. For starters, if $a \subseteq s$, $n \in \omega$, and $f:s^n \to s$, ‘$a$ is closed under $f$’ means precisely that for every $\langle. Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. The situation you describe, with a set v of values and a set f of functions, is referred to as v is closed under f. If a set of vectors is closed under addition, it means that if you perform vector addition on any two vectors within that set, the result is another. For example, the set of. A set is closed under (scalar) multiplication if you can multiply any two elements, and the result is still a number in the.
from www.storyofmathematics.com
If a set of vectors is closed under addition, it means that if you perform vector addition on any two vectors within that set, the result is another. Closure property states that when a set of numbers is closed under any arithmetic operation such as addition, subtraction, multiplication, and division, it means that when the operation. For example, the set of. Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. A set is closed under (scalar) multiplication if you can multiply any two elements, and the result is still a number in the. The situation you describe, with a set v of values and a set f of functions, is referred to as v is closed under f. For starters, if $a \subseteq s$, $n \in \omega$, and $f:s^n \to s$, ‘$a$ is closed under $f$’ means precisely that for every $\langle.
Closed Under Addition Property, Type of Numbers, and Examples The
Closed Under Meaning A set is closed under (scalar) multiplication if you can multiply any two elements, and the result is still a number in the. Closure property states that when a set of numbers is closed under any arithmetic operation such as addition, subtraction, multiplication, and division, it means that when the operation. If a set of vectors is closed under addition, it means that if you perform vector addition on any two vectors within that set, the result is another. A set is closed under (scalar) multiplication if you can multiply any two elements, and the result is still a number in the. For example, the set of. For starters, if $a \subseteq s$, $n \in \omega$, and $f:s^n \to s$, ‘$a$ is closed under $f$’ means precisely that for every $\langle. Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. The situation you describe, with a set v of values and a set f of functions, is referred to as v is closed under f.
From www.media4math.com
DefinitionClosure Property TopicsOdd Numbers and Closure Closed Under Meaning Closure property states that when a set of numbers is closed under any arithmetic operation such as addition, subtraction, multiplication, and division, it means that when the operation. If a set of vectors is closed under addition, it means that if you perform vector addition on any two vectors within that set, the result is another. For example, the set. Closed Under Meaning.
From www.youtube.com
How to Prove a Set of Functions is Closed Under Addition (Example with Closed Under Meaning A set is closed under (scalar) multiplication if you can multiply any two elements, and the result is still a number in the. If a set of vectors is closed under addition, it means that if you perform vector addition on any two vectors within that set, the result is another. For starters, if $a \subseteq s$, $n \in \omega$,. Closed Under Meaning.
From www.slideserve.com
PPT Theorem 1 Contextfree languages are closed under union Closed Under Meaning For example, the set of. Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. If a set of vectors is closed under addition, it means that if you perform vector addition on any two vectors within that set, the result is another. Closure property. Closed Under Meaning.
From slidesharetrick.blogspot.com
Closure Property Of Addition Definition slidesharetrick Closed Under Meaning For example, the set of. The situation you describe, with a set v of values and a set f of functions, is referred to as v is closed under f. Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. For starters, if $a \subseteq. Closed Under Meaning.
From www.slideserve.com
PPT Closure properties for regular languages PowerPoint Presentation Closed Under Meaning For starters, if $a \subseteq s$, $n \in \omega$, and $f:s^n \to s$, ‘$a$ is closed under $f$’ means precisely that for every $\langle. The situation you describe, with a set v of values and a set f of functions, is referred to as v is closed under f. Closure is when an operation (such as adding) on members of. Closed Under Meaning.
From englishgrammarhere.com
Opposite Of Under, Antonyms of Under, Meaning and Example Sentences Closed Under Meaning For example, the set of. Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. A set is closed under (scalar) multiplication if you can multiply any two elements, and the result is still a number in the. The situation you describe, with a set. Closed Under Meaning.
From www.vecteezy.com
Road closed Under construction tape warning banner vector 22231166 Closed Under Meaning The situation you describe, with a set v of values and a set f of functions, is referred to as v is closed under f. For example, the set of. Closure property states that when a set of numbers is closed under any arithmetic operation such as addition, subtraction, multiplication, and division, it means that when the operation. Closure is. Closed Under Meaning.
From www.storyofmathematics.com
Closed Under Addition Property, Type of Numbers, and Examples The Closed Under Meaning For starters, if $a \subseteq s$, $n \in \omega$, and $f:s^n \to s$, ‘$a$ is closed under $f$’ means precisely that for every $\langle. Closure property states that when a set of numbers is closed under any arithmetic operation such as addition, subtraction, multiplication, and division, it means that when the operation. For example, the set of. A set is. Closed Under Meaning.
From www.youtube.com
The Inverse Image of a CLOSED Set Under a Continuous Function is CLOSED Closed Under Meaning For starters, if $a \subseteq s$, $n \in \omega$, and $f:s^n \to s$, ‘$a$ is closed under $f$’ means precisely that for every $\langle. If a set of vectors is closed under addition, it means that if you perform vector addition on any two vectors within that set, the result is another. For example, the set of. Closure property states. Closed Under Meaning.
From www.pngaaa.com
Temporarily Closed C Under Construction Template For Page Is Closed Under Meaning For example, the set of. Closure property states that when a set of numbers is closed under any arithmetic operation such as addition, subtraction, multiplication, and division, it means that when the operation. For starters, if $a \subseteq s$, $n \in \omega$, and $f:s^n \to s$, ‘$a$ is closed under $f$’ means precisely that for every $\langle. The situation you. Closed Under Meaning.
From brainly.com
which set is closed under subtraction? Closed Under Meaning The situation you describe, with a set v of values and a set f of functions, is referred to as v is closed under f. For example, the set of. Closure property states that when a set of numbers is closed under any arithmetic operation such as addition, subtraction, multiplication, and division, it means that when the operation. Closure is. Closed Under Meaning.
From www.youtube.com
Closed Meaning YouTube Closed Under Meaning A set is closed under (scalar) multiplication if you can multiply any two elements, and the result is still a number in the. If a set of vectors is closed under addition, it means that if you perform vector addition on any two vectors within that set, the result is another. Closure property states that when a set of numbers. Closed Under Meaning.
From www.media4math.com
Student Tutorial Polynomial Concepts Definitions Media4Math Closed Under Meaning A set is closed under (scalar) multiplication if you can multiply any two elements, and the result is still a number in the. For starters, if $a \subseteq s$, $n \in \omega$, and $f:s^n \to s$, ‘$a$ is closed under $f$’ means precisely that for every $\langle. The situation you describe, with a set v of values and a set. Closed Under Meaning.
From slideplayer.com
Properties of Relational Logic ppt download Closed Under Meaning For starters, if $a \subseteq s$, $n \in \omega$, and $f:s^n \to s$, ‘$a$ is closed under $f$’ means precisely that for every $\langle. For example, the set of. The situation you describe, with a set v of values and a set f of functions, is referred to as v is closed under f. If a set of vectors is. Closed Under Meaning.
From englishgrammarhere.com
Sentences with Under, Under in a Sentence and Meaning English Grammar Closed Under Meaning Closure property states that when a set of numbers is closed under any arithmetic operation such as addition, subtraction, multiplication, and division, it means that when the operation. If a set of vectors is closed under addition, it means that if you perform vector addition on any two vectors within that set, the result is another. For example, the set. Closed Under Meaning.
From www.youtube.com
How to prove that context sensitive languages are closed under Closed Under Meaning A set is closed under (scalar) multiplication if you can multiply any two elements, and the result is still a number in the. If a set of vectors is closed under addition, it means that if you perform vector addition on any two vectors within that set, the result is another. For starters, if $a \subseteq s$, $n \in \omega$,. Closed Under Meaning.
From www.youtube.com
Determine if a set is closed under scalar multiplication Linear Closed Under Meaning Closure property states that when a set of numbers is closed under any arithmetic operation such as addition, subtraction, multiplication, and division, it means that when the operation. A set is closed under (scalar) multiplication if you can multiply any two elements, and the result is still a number in the. Closure is when an operation (such as adding) on. Closed Under Meaning.
From www.studocu.com
Closed CLOSED Definition A set is “closed” under operation if the Closed Under Meaning Closure property states that when a set of numbers is closed under any arithmetic operation such as addition, subtraction, multiplication, and division, it means that when the operation. The situation you describe, with a set v of values and a set f of functions, is referred to as v is closed under f. For example, the set of. For starters,. Closed Under Meaning.
From www.youtube.com
Let's Learn Discrete Math Sets Closed Under Addition and Closed Under Meaning If a set of vectors is closed under addition, it means that if you perform vector addition on any two vectors within that set, the result is another. For example, the set of. Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. A set. Closed Under Meaning.
From www.shutterstock.com
2,906 Temporarily Closed Images, Stock Photos & Vectors Shutterstock Closed Under Meaning A set is closed under (scalar) multiplication if you can multiply any two elements, and the result is still a number in the. For starters, if $a \subseteq s$, $n \in \omega$, and $f:s^n \to s$, ‘$a$ is closed under $f$’ means precisely that for every $\langle. Closure property states that when a set of numbers is closed under any. Closed Under Meaning.
From www.bradyid.com.au
We Are Temporarily Closed Under The Direction Of The Australian Closed Under Meaning A set is closed under (scalar) multiplication if you can multiply any two elements, and the result is still a number in the. If a set of vectors is closed under addition, it means that if you perform vector addition on any two vectors within that set, the result is another. Closure property states that when a set of numbers. Closed Under Meaning.
From www.slideserve.com
PPT Theorem 1 Contextfree languages are closed under union Closed Under Meaning A set is closed under (scalar) multiplication if you can multiply any two elements, and the result is still a number in the. For example, the set of. The situation you describe, with a set v of values and a set f of functions, is referred to as v is closed under f. Closure is when an operation (such as. Closed Under Meaning.
From www.vectorstock.com
Closed under construction cartoon Royalty Free Vector Image Closed Under Meaning The situation you describe, with a set v of values and a set f of functions, is referred to as v is closed under f. For starters, if $a \subseteq s$, $n \in \omega$, and $f:s^n \to s$, ‘$a$ is closed under $f$’ means precisely that for every $\langle. Closure is when an operation (such as adding) on members of. Closed Under Meaning.
From www.youtube.com
Tutorial Q2 Finite sets closed under addition and addition modulo Closed Under Meaning A set is closed under (scalar) multiplication if you can multiply any two elements, and the result is still a number in the. Closure property states that when a set of numbers is closed under any arithmetic operation such as addition, subtraction, multiplication, and division, it means that when the operation. For example, the set of. For starters, if $a. Closed Under Meaning.
From www.youtube.com
Determine whether a set is closed or open YouTube Closed Under Meaning The situation you describe, with a set v of values and a set f of functions, is referred to as v is closed under f. If a set of vectors is closed under addition, it means that if you perform vector addition on any two vectors within that set, the result is another. Closure property states that when a set. Closed Under Meaning.
From www.youtube.com
Regular Languages are Closed Under Union Theory of Computation YouTube Closed Under Meaning The situation you describe, with a set v of values and a set f of functions, is referred to as v is closed under f. For starters, if $a \subseteq s$, $n \in \omega$, and $f:s^n \to s$, ‘$a$ is closed under $f$’ means precisely that for every $\langle. Closure is when an operation (such as adding) on members of. Closed Under Meaning.
From www.youtube.com
Determining whether the language of a DFA is closed under reversal Closed Under Meaning If a set of vectors is closed under addition, it means that if you perform vector addition on any two vectors within that set, the result is another. For starters, if $a \subseteq s$, $n \in \omega$, and $f:s^n \to s$, ‘$a$ is closed under $f$’ means precisely that for every $\langle. Closure is when an operation (such as adding). Closed Under Meaning.
From www.youtube.com
Regular Languages Closed Under Complement Proof YouTube Closed Under Meaning Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. If a set of vectors is closed under addition, it means that if you perform vector addition on any two vectors within that set, the result is another. For starters, if $a \subseteq s$, $n. Closed Under Meaning.
From www.youtube.com
closure property of integers under multiplication Its Study time Closed Under Meaning A set is closed under (scalar) multiplication if you can multiply any two elements, and the result is still a number in the. For example, the set of. Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. Closure property states that when a set. Closed Under Meaning.
From www.youtube.com
How to Prove a Set is Closed Under Vector Addition YouTube Closed Under Meaning Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. A set is closed under (scalar) multiplication if you can multiply any two elements, and the result is still a number in the. The situation you describe, with a set v of values and a. Closed Under Meaning.
From www.slideserve.com
PPT Theorem 1 Contextfree languages are closed under union Closed Under Meaning Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. If a set of vectors is closed under addition, it means that if you perform vector addition on any two vectors within that set, the result is another. A set is closed under (scalar) multiplication. Closed Under Meaning.
From slideplayer.com
Context Sensitive Languages and Linear Bounded Automata ppt download Closed Under Meaning A set is closed under (scalar) multiplication if you can multiply any two elements, and the result is still a number in the. If a set of vectors is closed under addition, it means that if you perform vector addition on any two vectors within that set, the result is another. The situation you describe, with a set v of. Closed Under Meaning.
From slideplayer.com
CSE 105 theory of computation ppt download Closed Under Meaning Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. The situation you describe, with a set v of values and a set f of functions, is referred to as v is closed under f. For example, the set of. For starters, if $a \subseteq. Closed Under Meaning.
From www.youtube.com
Are contextfree languages in a^\*b^\* closed under complement? (2 Closed Under Meaning Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. The situation you describe, with a set v of values and a set f of functions, is referred to as v is closed under f. Closure property states that when a set of numbers is. Closed Under Meaning.
From dictionary.langeek.co
Definition & Meaning of "Under" LanGeek Closed Under Meaning A set is closed under (scalar) multiplication if you can multiply any two elements, and the result is still a number in the. If a set of vectors is closed under addition, it means that if you perform vector addition on any two vectors within that set, the result is another. Closure property states that when a set of numbers. Closed Under Meaning.