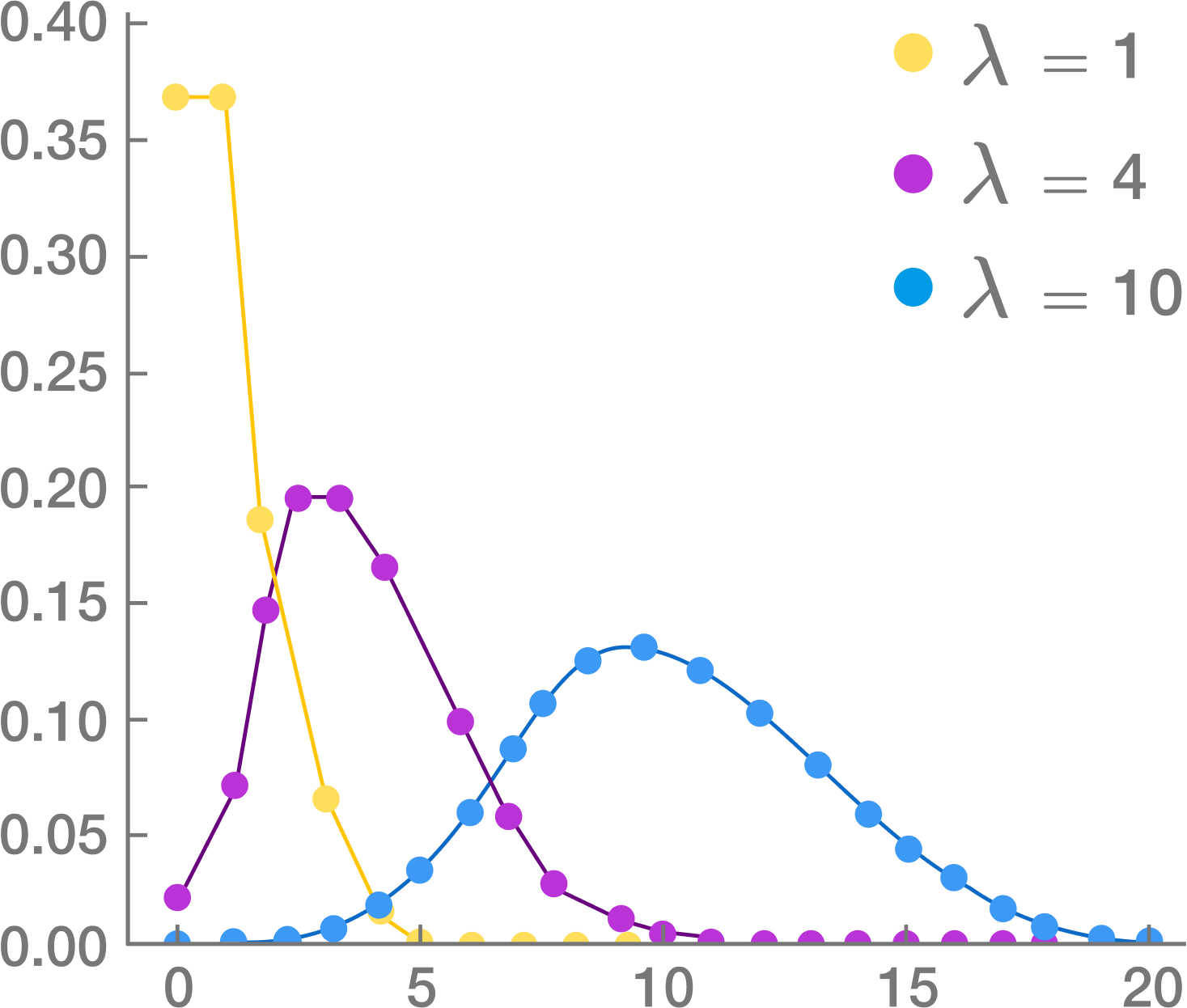
Poisson Process Interarrival Time Distribution . A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. Consider the times t1 and t2. Lecture outline • review of bernoulli process • definition of poisson process • distribution of. If $n(t)$ is a poisson process with rate $\lambda$, then the arrival times $t_1$, $t_2$, $\cdots$ have $gamma(n, \lambda)$. Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. The poisson process • readings: But this means that the poisson process, from time sonword is yet. Exponentials and independent of a(s). By shifting the origin to t1, the time of second arrival occurs at t2 − t1.
from brilliant.org
If $n(t)$ is a poisson process with rate $\lambda$, then the arrival times $t_1$, $t_2$, $\cdots$ have $gamma(n, \lambda)$. Exponentials and independent of a(s). The poisson process • readings: Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. Consider the times t1 and t2. Lecture outline • review of bernoulli process • definition of poisson process • distribution of. But this means that the poisson process, from time sonword is yet. By shifting the origin to t1, the time of second arrival occurs at t2 − t1.
Poisson Distribution Brilliant Math & Science Wiki
Poisson Process Interarrival Time Distribution Consider the times t1 and t2. Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. But this means that the poisson process, from time sonword is yet. Consider the times t1 and t2. The poisson process • readings: If $n(t)$ is a poisson process with rate $\lambda$, then the arrival times $t_1$, $t_2$, $\cdots$ have $gamma(n, \lambda)$. By shifting the origin to t1, the time of second arrival occurs at t2 − t1. Lecture outline • review of bernoulli process • definition of poisson process • distribution of. A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. Exponentials and independent of a(s).
From www.investopedia.com
Poisson Distribution Formula and Meaning in Finance Poisson Process Interarrival Time Distribution But this means that the poisson process, from time sonword is yet. If $n(t)$ is a poisson process with rate $\lambda$, then the arrival times $t_1$, $t_2$, $\cdots$ have $gamma(n, \lambda)$. By shifting the origin to t1, the time of second arrival occurs at t2 − t1. Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is. Poisson Process Interarrival Time Distribution.
From www.youtube.com
Interarrival time for a Poisson process YouTube Poisson Process Interarrival Time Distribution But this means that the poisson process, from time sonword is yet. A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. The poisson process • readings: Consider the times t1 and t2. Exponentials and independent of a(s). Lecture outline • review of bernoulli process • definition of poisson. Poisson Process Interarrival Time Distribution.
From www.slideserve.com
PPT The Poisson Process PowerPoint Presentation, free download ID Poisson Process Interarrival Time Distribution A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. But this means that the poisson process, from time sonword is yet. By shifting the origin to t1, the time of second arrival occurs at t2 − t1. If $n(t)$ is a poisson process with rate $\lambda$, then the. Poisson Process Interarrival Time Distribution.
From www.researchgate.net
Uniform distributionbased and Poisson processbased (that is Poisson Process Interarrival Time Distribution Consider the times t1 and t2. The poisson process • readings: Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. But this means that the poisson process, from time sonword is yet. Exponentials and independent of a(s). Lecture outline • review of bernoulli process • definition of poisson. Poisson Process Interarrival Time Distribution.
From slideplayer.com
Poisson Process and Related Distributions ppt download Poisson Process Interarrival Time Distribution Exponentials and independent of a(s). But this means that the poisson process, from time sonword is yet. Lecture outline • review of bernoulli process • definition of poisson process • distribution of. The poisson process • readings: Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. If $n(t)$. Poisson Process Interarrival Time Distribution.
From www.slideserve.com
PPT The Poisson Process PowerPoint Presentation, free download ID Poisson Process Interarrival Time Distribution But this means that the poisson process, from time sonword is yet. A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. The poisson process • readings: Consider the times t1 and t2. Lecture outline • review of bernoulli process • definition of poisson process • distribution of. Exponentials. Poisson Process Interarrival Time Distribution.
From slideplayer.com
Hydrologic Statistics ppt download Poisson Process Interarrival Time Distribution Consider the times t1 and t2. A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. By shifting the origin to t1, the time of second arrival occurs. Poisson Process Interarrival Time Distribution.
From math.stackexchange.com
probability How to prove the interarrival distribution of Poisson Poisson Process Interarrival Time Distribution The poisson process • readings: But this means that the poisson process, from time sonword is yet. Lecture outline • review of bernoulli process • definition of poisson process • distribution of. If $n(t)$ is a poisson process with rate $\lambda$, then the arrival times $t_1$, $t_2$, $\cdots$ have $gamma(n, \lambda)$. A poisson process is a simple and widely used. Poisson Process Interarrival Time Distribution.
From www.chegg.com
1. Consider a Poisson Process with intensity function Poisson Process Interarrival Time Distribution Lecture outline • review of bernoulli process • definition of poisson process • distribution of. By shifting the origin to t1, the time of second arrival occurs at t2 − t1. Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. Exponentials and independent of a(s). Consider the times. Poisson Process Interarrival Time Distribution.
From www.slideserve.com
PPT C12 The Poisson process PowerPoint Presentation, free download Poisson Process Interarrival Time Distribution Consider the times t1 and t2. Lecture outline • review of bernoulli process • definition of poisson process • distribution of. Exponentials and independent of a(s). The poisson process • readings: A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. If $n(t)$ is a poisson process with rate. Poisson Process Interarrival Time Distribution.
From www.slideserve.com
PPT Inside a Router PowerPoint Presentation, free download ID376487 Poisson Process Interarrival Time Distribution Exponentials and independent of a(s). Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. If $n(t)$ is a poisson process with rate $\lambda$, then the arrival times $t_1$, $t_2$, $\cdots$ have $gamma(n, \lambda)$. Consider the times t1 and t2. But this means that the poisson process, from time. Poisson Process Interarrival Time Distribution.
From www.slideserve.com
PPT The Poisson Process PowerPoint Presentation, free download ID Poisson Process Interarrival Time Distribution If $n(t)$ is a poisson process with rate $\lambda$, then the arrival times $t_1$, $t_2$, $\cdots$ have $gamma(n, \lambda)$. The poisson process • readings: By shifting the origin to t1, the time of second arrival occurs at t2 − t1. But this means that the poisson process, from time sonword is yet. Consider the times t1 and t2. A poisson. Poisson Process Interarrival Time Distribution.
From www.slideserve.com
PPT Inside a Router PowerPoint Presentation, free download ID376487 Poisson Process Interarrival Time Distribution If $n(t)$ is a poisson process with rate $\lambda$, then the arrival times $t_1$, $t_2$, $\cdots$ have $gamma(n, \lambda)$. A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. Exponentials and independent of a(s). Lecture outline • review of bernoulli process • definition of poisson process • distribution of.. Poisson Process Interarrival Time Distribution.
From www.slideserve.com
PPT The Poisson Process PowerPoint Presentation, free download ID Poisson Process Interarrival Time Distribution But this means that the poisson process, from time sonword is yet. Exponentials and independent of a(s). If $n(t)$ is a poisson process with rate $\lambda$, then the arrival times $t_1$, $t_2$, $\cdots$ have $gamma(n, \lambda)$. Consider the times t1 and t2. Lecture outline • review of bernoulli process • definition of poisson process • distribution of. By shifting the. Poisson Process Interarrival Time Distribution.
From www.researchgate.net
Updated interarrival time distributions (a) Weibull distribution with Poisson Process Interarrival Time Distribution Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. By shifting the origin to t1, the time of second arrival occurs at t2 − t1. A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. If $n(t)$. Poisson Process Interarrival Time Distribution.
From www.youtube.com
Inter arrival time of a Poisson Process follows exponential Poisson Process Interarrival Time Distribution But this means that the poisson process, from time sonword is yet. By shifting the origin to t1, the time of second arrival occurs at t2 − t1. Exponentials and independent of a(s). Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. Lecture outline • review of bernoulli. Poisson Process Interarrival Time Distribution.
From mpaldridge.github.io
Section 14 Poisson process with exponential holding times MATH2750 Poisson Process Interarrival Time Distribution Exponentials and independent of a(s). By shifting the origin to t1, the time of second arrival occurs at t2 − t1. Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. But this means that the poisson process, from time sonword is yet. The poisson process • readings: Lecture. Poisson Process Interarrival Time Distribution.
From www.youtube.com
Topic 08 04. Analyzing the Arrival Process Exponential Interarrival Poisson Process Interarrival Time Distribution The poisson process • readings: If $n(t)$ is a poisson process with rate $\lambda$, then the arrival times $t_1$, $t_2$, $\cdots$ have $gamma(n, \lambda)$. But this means that the poisson process, from time sonword is yet. A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. By shifting the. Poisson Process Interarrival Time Distribution.
From www.coursehero.com
[Solved] For a Poisson Process, show that the second inter arrival time Poisson Process Interarrival Time Distribution Consider the times t1 and t2. The poisson process • readings: Exponentials and independent of a(s). Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. Lecture outline • review of bernoulli process • definition of poisson process • distribution of. But this means that the poisson process, from. Poisson Process Interarrival Time Distribution.
From www.slideserve.com
PPT Exponential Distribution & Poisson Process PowerPoint Poisson Process Interarrival Time Distribution The poisson process • readings: But this means that the poisson process, from time sonword is yet. By shifting the origin to t1, the time of second arrival occurs at t2 − t1. A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. Consider the interarrival times of a. Poisson Process Interarrival Time Distribution.
From slideplayer.com
Probability, Statistics, and Traffic Theories ppt download Poisson Process Interarrival Time Distribution A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. By shifting the origin to t1, the time of second arrival occurs at t2 − t1. The poisson process • readings: Lecture outline • review of bernoulli process • definition of poisson process • distribution of. But this means. Poisson Process Interarrival Time Distribution.
From lambertyoullot.blogspot.com
Distribution of Arrival Time in Poisson Process Lambert Youllot Poisson Process Interarrival Time Distribution A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. If $n(t)$ is a poisson process with rate $\lambda$, then the arrival times $t_1$, $t_2$, $\cdots$ have $gamma(n, \lambda)$. But this means that the poisson process, from time sonword is yet. Consider the interarrival times of a poisson process. Poisson Process Interarrival Time Distribution.
From www.slideserve.com
PPT Chapter 2 Probability, Statistics and Flow Theory PowerPoint Poisson Process Interarrival Time Distribution Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. By shifting the origin to t1, the time of second arrival occurs at t2 − t1. Exponentials and. Poisson Process Interarrival Time Distribution.
From www.slideserve.com
PPT CPSC 531Input Modeling PowerPoint Presentation, free download Poisson Process Interarrival Time Distribution Consider the times t1 and t2. If $n(t)$ is a poisson process with rate $\lambda$, then the arrival times $t_1$, $t_2$, $\cdots$ have $gamma(n, \lambda)$. But this means that the poisson process, from time sonword is yet. Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. The poisson. Poisson Process Interarrival Time Distribution.
From www.youtube.com
Poisson process time between arrivals YouTube Poisson Process Interarrival Time Distribution A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. By shifting the origin to t1, the time of second arrival occurs at t2 − t1. If $n(t)$ is a poisson process with rate $\lambda$, then the arrival times $t_1$, $t_2$, $\cdots$ have $gamma(n, \lambda)$. Consider the times t1. Poisson Process Interarrival Time Distribution.
From brilliant.org
Poisson Distribution Brilliant Math & Science Wiki Poisson Process Interarrival Time Distribution Lecture outline • review of bernoulli process • definition of poisson process • distribution of. Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. If $n(t)$ is a poisson process with rate $\lambda$, then the arrival times $t_1$, $t_2$, $\cdots$ have $gamma(n, \lambda)$. Exponentials and independent of a(s).. Poisson Process Interarrival Time Distribution.
From www.slideserve.com
PPT Exponential Distribution & Poisson Process PowerPoint Poisson Process Interarrival Time Distribution Consider the times t1 and t2. Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. Lecture outline • review of bernoulli process • definition of poisson process. Poisson Process Interarrival Time Distribution.
From www.slideserve.com
PPT Poisson Process PowerPoint Presentation, free download ID9515578 Poisson Process Interarrival Time Distribution Exponentials and independent of a(s). Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. Lecture outline • review of bernoulli process • definition of poisson process • distribution of. The poisson process • readings: But this means that the poisson process, from time sonword is yet. By shifting. Poisson Process Interarrival Time Distribution.
From slideplayer.com
Introduction to Queuing Theory ppt download Poisson Process Interarrival Time Distribution The poisson process • readings: Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. Exponentials and independent of a(s). A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. Consider the times t1 and t2. If $n(t)$. Poisson Process Interarrival Time Distribution.
From www.slideserve.com
PPT The Poisson Process PowerPoint Presentation, free download ID Poisson Process Interarrival Time Distribution Consider the times t1 and t2. Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. Exponentials and independent of a(s). If $n(t)$ is a poisson process with rate $\lambda$, then the arrival times $t_1$, $t_2$, $\cdots$ have $gamma(n, \lambda)$. By shifting the origin to t1, the time of. Poisson Process Interarrival Time Distribution.
From slideplayer.com
Queueing Theory ppt download Poisson Process Interarrival Time Distribution A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. Exponentials and independent of a(s). Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. If $n(t)$ is a poisson process with rate $\lambda$, then the arrival times. Poisson Process Interarrival Time Distribution.
From www.slideserve.com
PPT Chapter 5 Statistical Models in Simulation PowerPoint Poisson Process Interarrival Time Distribution By shifting the origin to t1, the time of second arrival occurs at t2 − t1. Consider the times t1 and t2. A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. Exponentials and independent of a(s). If $n(t)$ is a poisson process with rate $\lambda$, then the arrival. Poisson Process Interarrival Time Distribution.
From www.youtube.com
The Poisson Process3 (Interarrival and Waiting Time Distributions Poisson Process Interarrival Time Distribution A poisson process is a simple and widely used stochastic process for modeling the times at which arrivals enter a system. By shifting the origin to t1, the time of second arrival occurs at t2 − t1. Lecture outline • review of bernoulli process • definition of poisson process • distribution of. If $n(t)$ is a poisson process with rate. Poisson Process Interarrival Time Distribution.
From www.slideserve.com
PPT Inside a Router PowerPoint Presentation, free download ID376487 Poisson Process Interarrival Time Distribution By shifting the origin to t1, the time of second arrival occurs at t2 − t1. Consider the interarrival times of a poisson process $(a_1, a_2,\dots)$, where $a_i$ is the elapsed time between arrival $i$ and arrival. Exponentials and independent of a(s). Lecture outline • review of bernoulli process • definition of poisson process • distribution of. The poisson process. Poisson Process Interarrival Time Distribution.
From lambertyoullot.blogspot.com
Distribution of Arrival Time in Poisson Process Lambert Youllot Poisson Process Interarrival Time Distribution But this means that the poisson process, from time sonword is yet. If $n(t)$ is a poisson process with rate $\lambda$, then the arrival times $t_1$, $t_2$, $\cdots$ have $gamma(n, \lambda)$. The poisson process • readings: Lecture outline • review of bernoulli process • definition of poisson process • distribution of. Consider the interarrival times of a poisson process $(a_1,. Poisson Process Interarrival Time Distribution.