Compact Boundary Example . You can for example consider the open unit ball $b_{<1}(0)$ with radius $1$ and the closed unit ball $b_{\leq1}(0)$ to get examples. The boundary of a compact set is therefore a. The interior of m is int m mi 2m exercise int m is a manifold w out boundary example m o i a eod id 17,1067 1 x lo d 10,1 if open in ri 2m o i int m. Being closed [but see above], compact sets contain all of their boundary points. A subset \(a\) of \(\mathbb{r}\) is compact if and only if it is closed and bounded. A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. A compact manifold is a manifold that is compact as a topological space. Suppose \(a\) is a compact subset of \(\mathbb{r}\).
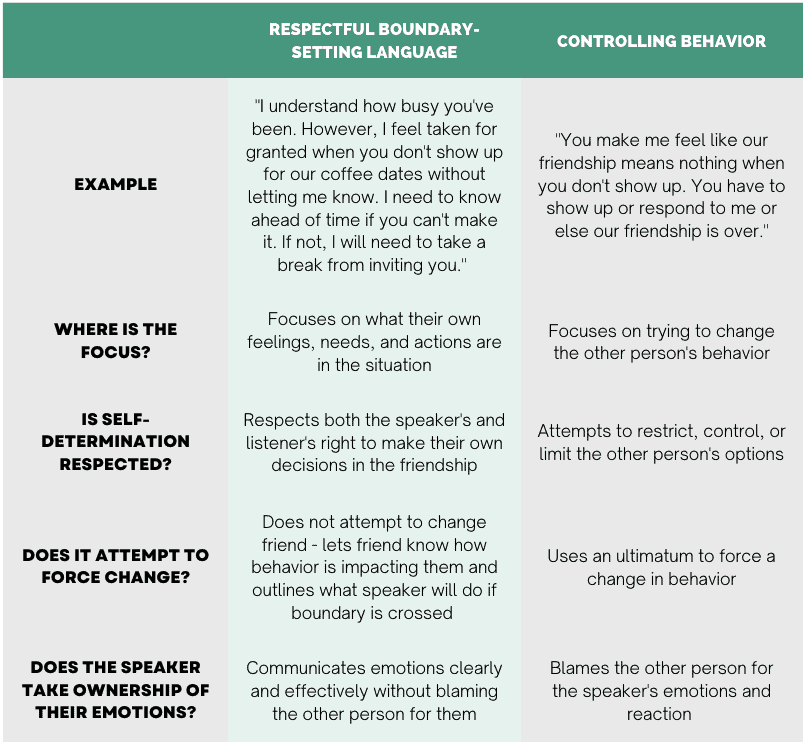
from www.tokyomentalhealth.com
You can for example consider the open unit ball $b_{<1}(0)$ with radius $1$ and the closed unit ball $b_{\leq1}(0)$ to get examples. A compact manifold is a manifold that is compact as a topological space. A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. The interior of m is int m mi 2m exercise int m is a manifold w out boundary example m o i a eod id 17,1067 1 x lo d 10,1 if open in ri 2m o i int m. A subset \(a\) of \(\mathbb{r}\) is compact if and only if it is closed and bounded. The boundary of a compact set is therefore a. Being closed [but see above], compact sets contain all of their boundary points. Suppose \(a\) is a compact subset of \(\mathbb{r}\).
setting boundaries table TOKYO MENTAL HEALTH
Compact Boundary Example Suppose \(a\) is a compact subset of \(\mathbb{r}\). The boundary of a compact set is therefore a. Being closed [but see above], compact sets contain all of their boundary points. A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. You can for example consider the open unit ball $b_{<1}(0)$ with radius $1$ and the closed unit ball $b_{\leq1}(0)$ to get examples. The interior of m is int m mi 2m exercise int m is a manifold w out boundary example m o i a eod id 17,1067 1 x lo d 10,1 if open in ri 2m o i int m. A subset \(a\) of \(\mathbb{r}\) is compact if and only if it is closed and bounded. A compact manifold is a manifold that is compact as a topological space. Suppose \(a\) is a compact subset of \(\mathbb{r}\).
From transportgeography.org
Types of International Boundaries The Geography of Transport Systems Compact Boundary Example A subset \(a\) of \(\mathbb{r}\) is compact if and only if it is closed and bounded. Being closed [but see above], compact sets contain all of their boundary points. You can for example consider the open unit ball $b_{<1}(0)$ with radius $1$ and the closed unit ball $b_{\leq1}(0)$ to get examples. The boundary of a compact set is therefore a.. Compact Boundary Example.
From www.geologyin.com
The Differences between Convergent and Divergent Boundaries Geology In Compact Boundary Example Being closed [but see above], compact sets contain all of their boundary points. You can for example consider the open unit ball $b_{<1}(0)$ with radius $1$ and the closed unit ball $b_{\leq1}(0)$ to get examples. The boundary of a compact set is therefore a. A compact operator is one which maps the unit ball (and hence any bounded subset) of. Compact Boundary Example.
From www.diesicounseling.com
A Guide to Setting Healthy Boundaries Compact Boundary Example A subset \(a\) of \(\mathbb{r}\) is compact if and only if it is closed and bounded. Being closed [but see above], compact sets contain all of their boundary points. Suppose \(a\) is a compact subset of \(\mathbb{r}\). A compact manifold is a manifold that is compact as a topological space. A compact operator is one which maps the unit ball. Compact Boundary Example.
From www.alamy.com
Divergent plate boundary with explanation illustration Stock Vector Compact Boundary Example Suppose \(a\) is a compact subset of \(\mathbb{r}\). A compact manifold is a manifold that is compact as a topological space. Being closed [but see above], compact sets contain all of their boundary points. You can for example consider the open unit ball $b_{<1}(0)$ with radius $1$ and the closed unit ball $b_{\leq1}(0)$ to get examples. A compact operator is. Compact Boundary Example.
From www.slideserve.com
PPT Convergent Boundary with Subduction PowerPoint Presentation, free Compact Boundary Example Being closed [but see above], compact sets contain all of their boundary points. The interior of m is int m mi 2m exercise int m is a manifold w out boundary example m o i a eod id 17,1067 1 x lo d 10,1 if open in ri 2m o i int m. The boundary of a compact set is. Compact Boundary Example.
From earthsurface.readthedocs.io
Tectonics, passive margins & dynamic topography — EarthSurface 0.0.1 Compact Boundary Example A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. The boundary of a compact set is therefore a. You can for example consider the open unit ball $b_{<1}(0)$ with radius $1$ and the closed unit ball $b_{\leq1}(0)$ to get examples. Suppose \(a\) is. Compact Boundary Example.
From studylib.net
Compact States Efficient Compact Boundary Example The boundary of a compact set is therefore a. A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. A subset \(a\) of \(\mathbb{r}\) is compact if and only if it is closed and bounded. Suppose \(a\) is a compact subset of \(\mathbb{r}\). Being. Compact Boundary Example.
From www.slideserve.com
PPT Project Boundaries PowerPoint Presentation, free download ID Compact Boundary Example Suppose \(a\) is a compact subset of \(\mathbb{r}\). A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. The interior of m is int m mi 2m exercise int m is a manifold w out boundary example m o i a eod id 17,1067. Compact Boundary Example.
From www.pinterest.com
Understanding the Six Types of Boundaries Compact Boundary Example The boundary of a compact set is therefore a. You can for example consider the open unit ball $b_{<1}(0)$ with radius $1$ and the closed unit ball $b_{\leq1}(0)$ to get examples. A subset \(a\) of \(\mathbb{r}\) is compact if and only if it is closed and bounded. Being closed [but see above], compact sets contain all of their boundary points.. Compact Boundary Example.
From engineerexcel.com
Boundary Layer in Pipe Flow A Comprehensive Analysis EngineerExcel Compact Boundary Example A compact manifold is a manifold that is compact as a topological space. You can for example consider the open unit ball $b_{<1}(0)$ with radius $1$ and the closed unit ball $b_{\leq1}(0)$ to get examples. Suppose \(a\) is a compact subset of \(\mathbb{r}\). A subset \(a\) of \(\mathbb{r}\) is compact if and only if it is closed and bounded. The. Compact Boundary Example.
From www.youtube.com
EMA5001 L1004 Twin boundaries YouTube Compact Boundary Example Suppose \(a\) is a compact subset of \(\mathbb{r}\). A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. A subset \(a\) of \(\mathbb{r}\) is compact if and only if it is closed and bounded. The interior of m is int m mi 2m exercise. Compact Boundary Example.
From www.slideserve.com
PPT Plate Boundary PowerPoint Presentation, free download ID2497701 Compact Boundary Example A compact manifold is a manifold that is compact as a topological space. The interior of m is int m mi 2m exercise int m is a manifold w out boundary example m o i a eod id 17,1067 1 x lo d 10,1 if open in ri 2m o i int m. You can for example consider the open. Compact Boundary Example.
From www.thoughtco.com
What Is a Convergent Plate Boundary? Compact Boundary Example A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. A subset \(a\) of \(\mathbb{r}\) is compact if and only if it is closed and bounded. The boundary of a compact set is therefore a. You can for example consider the open unit ball. Compact Boundary Example.
From www.slideserve.com
PPT Formation of Boundaries and Political Divisions PowerPoint Compact Boundary Example A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. A compact manifold is a manifold that is compact as a topological space. Being closed [but see above], compact sets contain all of their boundary points. The interior of m is int m mi. Compact Boundary Example.
From www.zmescience.com
Convergent boundaries the tectonic forces that shape the Earth Compact Boundary Example You can for example consider the open unit ball $b_{<1}(0)$ with radius $1$ and the closed unit ball $b_{\leq1}(0)$ to get examples. A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. Being closed [but see above], compact sets contain all of their boundary. Compact Boundary Example.
From www.slideserve.com
PPT Political Geography PowerPoint Presentation, free download ID Compact Boundary Example Being closed [but see above], compact sets contain all of their boundary points. Suppose \(a\) is a compact subset of \(\mathbb{r}\). A compact manifold is a manifold that is compact as a topological space. A subset \(a\) of \(\mathbb{r}\) is compact if and only if it is closed and bounded. The interior of m is int m mi 2m exercise. Compact Boundary Example.
From geologyjosh.weebly.com
Types of Boundaries Geology with Josh Compact Boundary Example A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. You can for example consider the open unit ball $b_{<1}(0)$ with radius $1$ and the closed unit ball $b_{\leq1}(0)$ to get examples. The boundary of a compact set is therefore a. Being closed [but. Compact Boundary Example.
From helpfulprofessor.com
Subsequent Boundary Definition & Examples (Human Geography) (2024) Compact Boundary Example A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. A subset \(a\) of \(\mathbb{r}\) is compact if and only if it is closed and bounded. You can for example consider the open unit ball $b_{<1}(0)$ with radius $1$ and the closed unit ball. Compact Boundary Example.
From paintingvalley.com
Divergent Boundary Sketch at Explore collection of Compact Boundary Example Suppose \(a\) is a compact subset of \(\mathbb{r}\). The interior of m is int m mi 2m exercise int m is a manifold w out boundary example m o i a eod id 17,1067 1 x lo d 10,1 if open in ri 2m o i int m. Being closed [but see above], compact sets contain all of their boundary. Compact Boundary Example.
From crossroadsindy.com
Boundaries Definition and Types of Boundaries Compact Boundary Example The interior of m is int m mi 2m exercise int m is a manifold w out boundary example m o i a eod id 17,1067 1 x lo d 10,1 if open in ri 2m o i int m. A compact manifold is a manifold that is compact as a topological space. The boundary of a compact set is. Compact Boundary Example.
From study.com
Convergent Boundary Definition, Features & Examples Lesson Compact Boundary Example Being closed [but see above], compact sets contain all of their boundary points. Suppose \(a\) is a compact subset of \(\mathbb{r}\). A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. A compact manifold is a manifold that is compact as a topological space.. Compact Boundary Example.
From www.tokyomentalhealth.com
setting boundaries table TOKYO MENTAL HEALTH Compact Boundary Example A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. A compact manifold is a manifold that is compact as a topological space. Suppose \(a\) is a compact subset of \(\mathbb{r}\). Being closed [but see above], compact sets contain all of their boundary points.. Compact Boundary Example.
From present5.com
Five Basic Shapes of States Compact Compact Boundary Example You can for example consider the open unit ball $b_{<1}(0)$ with radius $1$ and the closed unit ball $b_{\leq1}(0)$ to get examples. Suppose \(a\) is a compact subset of \(\mathbb{r}\). The boundary of a compact set is therefore a. The interior of m is int m mi 2m exercise int m is a manifold w out boundary example m o. Compact Boundary Example.
From study.com
What is a Transform Boundary? Transform Boundary Examples & Features Compact Boundary Example The interior of m is int m mi 2m exercise int m is a manifold w out boundary example m o i a eod id 17,1067 1 x lo d 10,1 if open in ri 2m o i int m. A subset \(a\) of \(\mathbb{r}\) is compact if and only if it is closed and bounded. You can for example. Compact Boundary Example.
From www.dexform.com
Boundary Line Agreement and Special Warranty Deed in Word and Pdf formats Compact Boundary Example A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. A compact manifold is a manifold that is compact as a topological space. Being closed [but see above], compact sets contain all of their boundary points. Suppose \(a\) is a compact subset of \(\mathbb{r}\).. Compact Boundary Example.
From wilmarcarrilho.blogspot.com
Antecedent Boundary Origin Compact Boundary Example You can for example consider the open unit ball $b_{<1}(0)$ with radius $1$ and the closed unit ball $b_{\leq1}(0)$ to get examples. A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. The boundary of a compact set is therefore a. Suppose \(a\) is. Compact Boundary Example.
From www.slideserve.com
PPT Political Geography PowerPoint Presentation, free download ID Compact Boundary Example The boundary of a compact set is therefore a. Suppose \(a\) is a compact subset of \(\mathbb{r}\). A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. A compact manifold is a manifold that is compact as a topological space. The interior of m. Compact Boundary Example.
From slideplayer.com
Plate Tectonics Shake, Rattle, & Roll!. ppt download Compact Boundary Example The boundary of a compact set is therefore a. A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. A compact manifold is a manifold that is compact as a topological space. You can for example consider the open unit ball $b_{<1}(0)$ with radius. Compact Boundary Example.
From www.showme.com
Transform Boundary Science ShowMe Compact Boundary Example A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. The interior of m is int m mi 2m exercise int m is a manifold w out boundary example m o i a eod id 17,1067 1 x lo d 10,1 if open in. Compact Boundary Example.
From viewerhome.weebly.com
Antecedent boundary example viewerhome Compact Boundary Example Being closed [but see above], compact sets contain all of their boundary points. A subset \(a\) of \(\mathbb{r}\) is compact if and only if it is closed and bounded. Suppose \(a\) is a compact subset of \(\mathbb{r}\). A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set. Compact Boundary Example.
From www.pinterest.com
Understanding Transform Boundary Definition and Useful Examples Compact Boundary Example Suppose \(a\) is a compact subset of \(\mathbb{r}\). A compact manifold is a manifold that is compact as a topological space. Being closed [but see above], compact sets contain all of their boundary points. The boundary of a compact set is therefore a. A compact operator is one which maps the unit ball (and hence any bounded subset) of h. Compact Boundary Example.
From www.slideserve.com
PPT Territorial Morphology PowerPoint Presentation, free download Compact Boundary Example A compact manifold is a manifold that is compact as a topological space. Suppose \(a\) is a compact subset of \(\mathbb{r}\). A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. Being closed [but see above], compact sets contain all of their boundary points.. Compact Boundary Example.
From wildwestsoutherngirl.blogspot.com
Antecedent Boundary Def Compact Boundary Example The interior of m is int m mi 2m exercise int m is a manifold w out boundary example m o i a eod id 17,1067 1 x lo d 10,1 if open in ri 2m o i int m. Suppose \(a\) is a compact subset of \(\mathbb{r}\). Being closed [but see above], compact sets contain all of their boundary. Compact Boundary Example.
From kizaselection.weebly.com
kizaselection Blog Compact Boundary Example A compact operator is one which maps the unit ball (and hence any bounded subset) of h onto a precompact set, a set with compact closure. A compact manifold is a manifold that is compact as a topological space. The interior of m is int m mi 2m exercise int m is a manifold w out boundary example m o. Compact Boundary Example.
From www.thegeographeronline.net
Plate Tectonics THE GEOGRAPHER ONLINE Compact Boundary Example Being closed [but see above], compact sets contain all of their boundary points. A subset \(a\) of \(\mathbb{r}\) is compact if and only if it is closed and bounded. A compact manifold is a manifold that is compact as a topological space. The interior of m is int m mi 2m exercise int m is a manifold w out boundary. Compact Boundary Example.