Frequency And Tension Relationship at Leo Baca blog

Frequency And Tension Relationship. Consider a small element of the string with a mass equal to δm = μδx δ m = μ δ x. The hanging mass provides the tension in the string, and the speed of the waves on the string is proportional to the square root of the tension divided by the linear mass density. When you change the tension on the string, you are changing the. Waves of the same frequency that interfere can be generated by propagating waves along a string, as the reflected waves from the end of the string will have the same. To see how the speed of a wave on a string depends on the tension and the linear density, consider a pulse sent down a taut string (figure 16.4.1 16.4. This is obviously not an ideal string since the best straight line fit of the data of frequency vs square root of tension would not pass through zero. As we saw in the last section, when waves have the same frequency, it is possible for them to interfere completely, either destructively or constructively. In this experiment, you will explore the relationship between string length, wavelength, frequency, linear density, and string tension in a. I know my strings resonant frequency: When the taut string is at rest at the equilibrium position, the tension in the string ft f t is constant. From that, how do i calculate. When the wave relationship is applied to a stretched string, it is seen that resonant standing wave modes are produced. The exact relationship between frequency and wavelength is f = c/λ.

When you change the tension on the string, you are changing the. When the taut string is at rest at the equilibrium position, the tension in the string ft f t is constant. From that, how do i calculate. To see how the speed of a wave on a string depends on the tension and the linear density, consider a pulse sent down a taut string (figure 16.4.1 16.4. Consider a small element of the string with a mass equal to δm = μδx δ m = μ δ x. In this experiment, you will explore the relationship between string length, wavelength, frequency, linear density, and string tension in a. As we saw in the last section, when waves have the same frequency, it is possible for them to interfere completely, either destructively or constructively. The hanging mass provides the tension in the string, and the speed of the waves on the string is proportional to the square root of the tension divided by the linear mass density. Waves of the same frequency that interfere can be generated by propagating waves along a string, as the reflected waves from the end of the string will have the same. I know my strings resonant frequency:

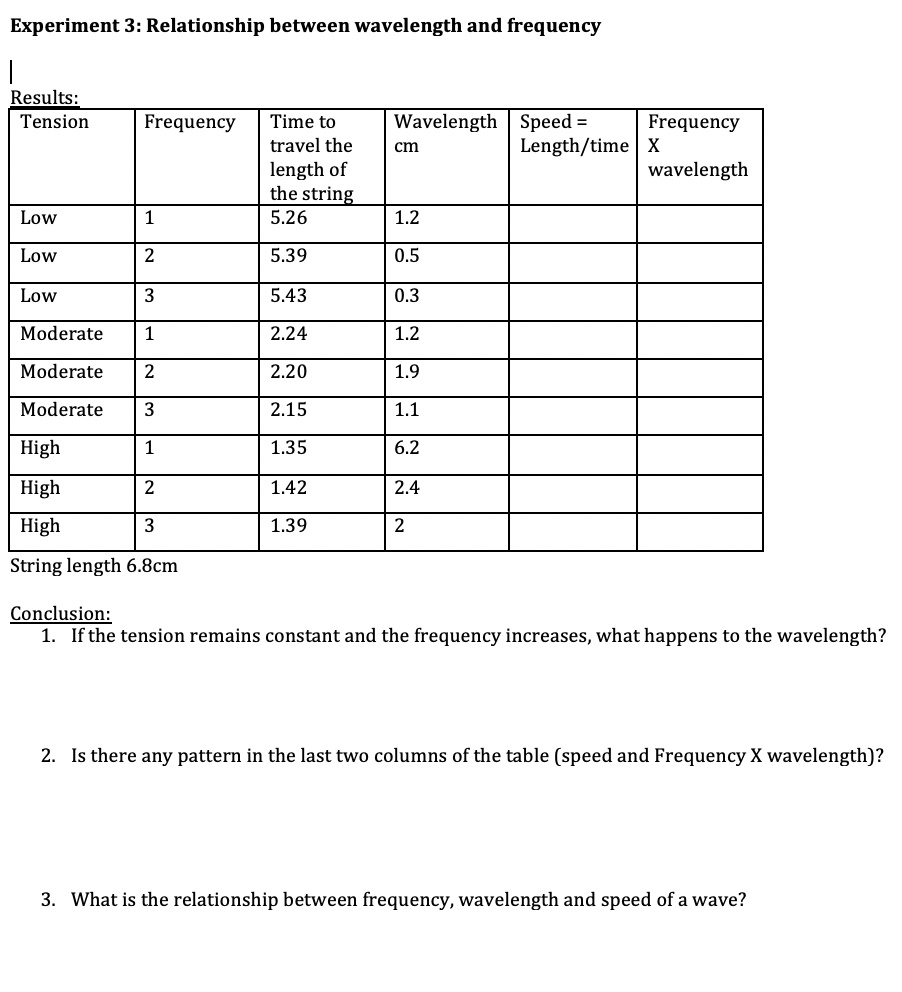
Experiment 3 Relationship between wavelength and frequency Results

Frequency And Tension Relationship Consider a small element of the string with a mass equal to δm = μδx δ m = μ δ x. When you change the tension on the string, you are changing the. When the wave relationship is applied to a stretched string, it is seen that resonant standing wave modes are produced. This is obviously not an ideal string since the best straight line fit of the data of frequency vs square root of tension would not pass through zero. The exact relationship between frequency and wavelength is f = c/λ. The hanging mass provides the tension in the string, and the speed of the waves on the string is proportional to the square root of the tension divided by the linear mass density. To see how the speed of a wave on a string depends on the tension and the linear density, consider a pulse sent down a taut string (figure 16.4.1 16.4. In this experiment, you will explore the relationship between string length, wavelength, frequency, linear density, and string tension in a. Consider a small element of the string with a mass equal to δm = μδx δ m = μ δ x. I know my strings resonant frequency: Waves of the same frequency that interfere can be generated by propagating waves along a string, as the reflected waves from the end of the string will have the same. When the taut string is at rest at the equilibrium position, the tension in the string ft f t is constant. From that, how do i calculate. As we saw in the last section, when waves have the same frequency, it is possible for them to interfere completely, either destructively or constructively.