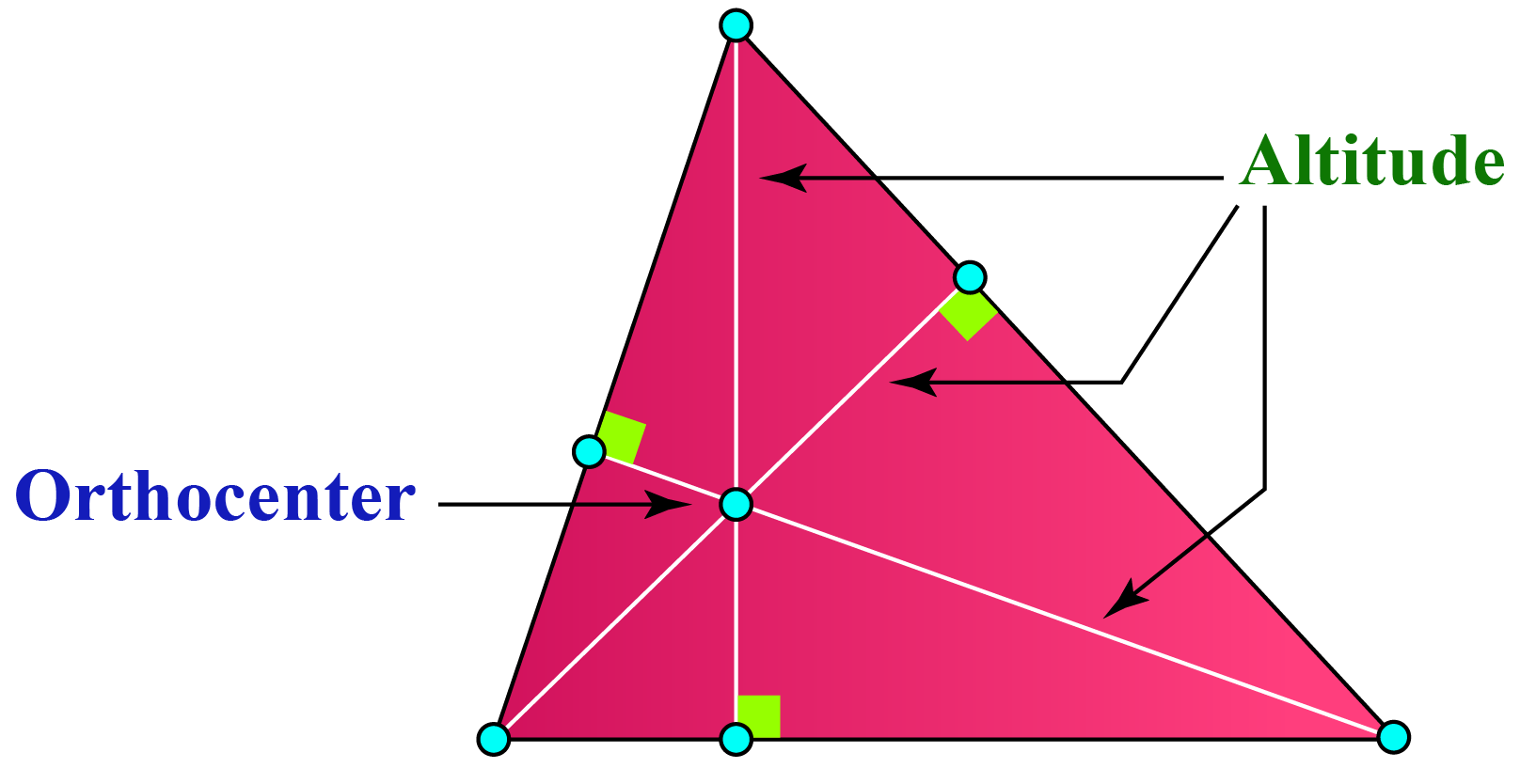
Equilateral Triangle Altitude Proof . Height of equilateral triangle formula proof. To derive the formula of altitude of an equilateral triangle, two different methods can be used. An equilateral triangle is a triangle with all three equal sides and each angle measures up to 60 degrees. Therefore, we will apply the pythagoras theorem, which. Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. Learn formulas of area, perimeter and. It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle. The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side. For any point p within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle.
from www.cuemath.com
Height of equilateral triangle formula proof. An equilateral triangle is a triangle with all three equal sides and each angle measures up to 60 degrees. It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle. Therefore, we will apply the pythagoras theorem, which. To derive the formula of altitude of an equilateral triangle, two different methods can be used. The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side. Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. Learn formulas of area, perimeter and. For any point p within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle.
Altitude of a Triangle Cuemath
Equilateral Triangle Altitude Proof Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. For any point p within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle. It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle. Height of equilateral triangle formula proof. Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. Therefore, we will apply the pythagoras theorem, which. The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side. An equilateral triangle is a triangle with all three equal sides and each angle measures up to 60 degrees. To derive the formula of altitude of an equilateral triangle, two different methods can be used. Learn formulas of area, perimeter and.
From www.teachoo.com
Altitude of a triangle Examples with Figures Teachoo Equilateral Triangle Altitude Proof Learn formulas of area, perimeter and. For any point p within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle. The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side. Therefore, we will apply the pythagoras theorem,. Equilateral Triangle Altitude Proof.
From arturo-ksherman.blogspot.com
Does the Altitude of an Equilateral Triangle Bisect the Base Equilateral Triangle Altitude Proof Learn formulas of area, perimeter and. Height of equilateral triangle formula proof. Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. Therefore, we will apply the pythagoras theorem, which. To derive the formula of altitude of an equilateral triangle, two different methods can be used. It is interesting to note that. Equilateral Triangle Altitude Proof.
From byjus.com
40. If the altitude of an equilateral triangle is x cmthen the area is Equilateral Triangle Altitude Proof To derive the formula of altitude of an equilateral triangle, two different methods can be used. For any point p within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle. Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. It. Equilateral Triangle Altitude Proof.
From www.cuemath.com
Altitude of a Triangle Cuemath Equilateral Triangle Altitude Proof The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side. For any point p within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle. Because the equilateral triangle is, in some sense, the simplest polygon, many typically. Equilateral Triangle Altitude Proof.
From ar.inspiredpencil.com
Equilateral Triangle Showing Three Altitudes Equilateral Triangle Altitude Proof To derive the formula of altitude of an equilateral triangle, two different methods can be used. Learn formulas of area, perimeter and. Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. An equilateral triangle is a triangle with all three equal sides and each angle measures up to 60 degrees. The. Equilateral Triangle Altitude Proof.
From byjus.com
If all the altitudes of a triangle are equal , prove that the triangle Equilateral Triangle Altitude Proof Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side. Therefore, we will apply the pythagoras theorem, which. To derive the formula of altitude of an equilateral triangle, two different. Equilateral Triangle Altitude Proof.
From ar.inspiredpencil.com
Equilateral Triangle Showing Three Altitudes Equilateral Triangle Altitude Proof To derive the formula of altitude of an equilateral triangle, two different methods can be used. For any point p within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle. It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle.. Equilateral Triangle Altitude Proof.
From study.com
Equilateral Triangle Definition, Properties & Measurements Lesson Equilateral Triangle Altitude Proof The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side. Therefore, we will apply the pythagoras theorem, which. Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. An equilateral triangle is a triangle with all three equal sides and. Equilateral Triangle Altitude Proof.
From ar.inspiredpencil.com
Equilateral Triangle Showing Three Altitudes Equilateral Triangle Altitude Proof The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side. Therefore, we will apply the pythagoras theorem, which. For any point p within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle. To derive the formula of. Equilateral Triangle Altitude Proof.
From arturo-ksherman.blogspot.com
Does the Altitude of an Equilateral Triangle Bisect the Base Equilateral Triangle Altitude Proof To derive the formula of altitude of an equilateral triangle, two different methods can be used. Therefore, we will apply the pythagoras theorem, which. The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side. Height of equilateral triangle formula proof. Learn formulas of area, perimeter and. Because the. Equilateral Triangle Altitude Proof.
From mathinschool.com
Derivation of Formula for Altitude of an Equilateral Triangle Equilateral Triangle Altitude Proof Height of equilateral triangle formula proof. Therefore, we will apply the pythagoras theorem, which. An equilateral triangle is a triangle with all three equal sides and each angle measures up to 60 degrees. Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. To derive the formula of altitude of an equilateral. Equilateral Triangle Altitude Proof.
From byjus.com
ABC is an equilateral triangle of side 2a. Find each of its altitudes. Equilateral Triangle Altitude Proof For any point p within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle. Learn formulas of area, perimeter and. The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side. To derive the formula of altitude of. Equilateral Triangle Altitude Proof.
From byjus.com
The length of an altitude of an equilateral triangle having side length Equilateral Triangle Altitude Proof The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side. Learn formulas of area, perimeter and. Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. For any point p within an equilateral triangle, the sum of the perpendiculars to. Equilateral Triangle Altitude Proof.
From brilliant.org
Properties of Equilateral Triangles Brilliant Math & Science Wiki Equilateral Triangle Altitude Proof Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side. It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle. Therefore,. Equilateral Triangle Altitude Proof.
From ar.inspiredpencil.com
Equilateral Triangle Showing Three Altitudes Equilateral Triangle Altitude Proof An equilateral triangle is a triangle with all three equal sides and each angle measures up to 60 degrees. Height of equilateral triangle formula proof. To derive the formula of altitude of an equilateral triangle, two different methods can be used. It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle.. Equilateral Triangle Altitude Proof.
From byjus.com
61. Construct an equilateral triangle of altitude 6m. Equilateral Triangle Altitude Proof For any point p within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle. It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle. To derive the formula of altitude of an equilateral triangle, two different methods can be used.. Equilateral Triangle Altitude Proof.
From swatishifu.blogspot.com
Altitude of an equilateral triangle Equilateral Triangle Altitude Proof The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side. Therefore, we will apply the pythagoras theorem, which. Height of equilateral triangle formula proof. An equilateral triangle is a triangle with all three equal sides and each angle measures up to 60 degrees. To derive the formula of. Equilateral Triangle Altitude Proof.
From www.youtube.com
Find the length of an altitude of an equilateral triangle of side 8cm Equilateral Triangle Altitude Proof Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. Therefore, we will apply the pythagoras theorem, which. For any point p within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle. The altitude or height of an equilateral triangle is. Equilateral Triangle Altitude Proof.
From brilliant.org
Properties of Equilateral Triangles Brilliant Math & Science Wiki Equilateral Triangle Altitude Proof An equilateral triangle is a triangle with all three equal sides and each angle measures up to 60 degrees. To derive the formula of altitude of an equilateral triangle, two different methods can be used. For any point p within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle.. Equilateral Triangle Altitude Proof.
From www.topperlearning.com
What is the length of an altitude of an equilateral triangle with side Equilateral Triangle Altitude Proof To derive the formula of altitude of an equilateral triangle, two different methods can be used. Height of equilateral triangle formula proof. Learn formulas of area, perimeter and. Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. The altitude or height of an equilateral triangle is the line segment from a. Equilateral Triangle Altitude Proof.
From www.chilimath.com
Area of Equilateral Triangle Derivation, Formula & Examples ChiliMath Equilateral Triangle Altitude Proof Learn formulas of area, perimeter and. Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. Therefore, we will apply the pythagoras theorem, which. For any point p within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle. An equilateral triangle. Equilateral Triangle Altitude Proof.
From www.youtube.com
If the altitude of an equilateral triangle is `12sqrt3 cm`, find its Equilateral Triangle Altitude Proof Therefore, we will apply the pythagoras theorem, which. Height of equilateral triangle formula proof. Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. To derive the formula of altitude of an equilateral triangle, two different methods can be used. For any point p within an equilateral triangle, the sum of the. Equilateral Triangle Altitude Proof.
From www.youtube.com
Proof Height of an Equilateral Triangle Formula YouTube Equilateral Triangle Altitude Proof Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. Therefore, we will apply the pythagoras theorem, which. An equilateral triangle is a triangle with all three equal sides and each angle measures up to 60 degrees. Learn formulas of area, perimeter and. For any point p within an equilateral triangle, the. Equilateral Triangle Altitude Proof.
From www.quora.com
In an equilateral triangle, the length of the altitude is 6 cm. What is Equilateral Triangle Altitude Proof Therefore, we will apply the pythagoras theorem, which. Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle. The altitude or height of an equilateral triangle is the line segment from a vertex. Equilateral Triangle Altitude Proof.
From mathmonks.com
Equilateral Triangle Definition, Properties, Formulas Equilateral Triangle Altitude Proof Height of equilateral triangle formula proof. To derive the formula of altitude of an equilateral triangle, two different methods can be used. It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle. An equilateral triangle is a triangle with all three equal sides and each angle measures up to 60 degrees.. Equilateral Triangle Altitude Proof.
From www.cuemath.com
Perimeter of Equilateral Triangle Formula, Definition, Examples Equilateral Triangle Altitude Proof Height of equilateral triangle formula proof. It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle. An equilateral triangle is a triangle with all three equal sides and each angle measures up to 60 degrees. To derive the formula of altitude of an equilateral triangle, two different methods can be used.. Equilateral Triangle Altitude Proof.
From owlcation.com
A Full Guide to the 306090 Triangle (With Formulas and Examples Equilateral Triangle Altitude Proof To derive the formula of altitude of an equilateral triangle, two different methods can be used. Therefore, we will apply the pythagoras theorem, which. Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. An equilateral triangle is a triangle with all three equal sides and each angle measures up to 60. Equilateral Triangle Altitude Proof.
From ar.inspiredpencil.com
Equilateral Triangle Showing Three Altitudes Equilateral Triangle Altitude Proof It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle. An equilateral triangle is a triangle with all three equal sides and each angle measures up to 60 degrees. To derive the formula of altitude of an equilateral triangle, two different methods can be used. Therefore, we will apply the pythagoras. Equilateral Triangle Altitude Proof.
From www.youtube.com
Equilateral Triangle Altitude And Area Formula Proof Equilateral Triangle Altitude Proof The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side. It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle. For any point p within an equilateral triangle, the sum of the perpendiculars to the three sides is equal. Equilateral Triangle Altitude Proof.
From www.cuemath.com
How can you Prove a Triangle is an Equilateral Triangle?[solved] Equilateral Triangle Altitude Proof It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle. Therefore, we will apply the pythagoras theorem, which. For any point p within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle. Height of equilateral triangle formula proof. Because the. Equilateral Triangle Altitude Proof.
From byjus.com
Is it possible to construct an equilateral triangle , if its altitude Equilateral Triangle Altitude Proof Learn formulas of area, perimeter and. Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. Therefore, we will apply the pythagoras theorem, which. The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side. An equilateral triangle is a triangle. Equilateral Triangle Altitude Proof.
From mathmonks.com
Equilateral Triangle Definition, Properties, Formulas Equilateral Triangle Altitude Proof It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle. Learn formulas of area, perimeter and. Because the equilateral triangle is, in some sense, the simplest polygon, many typically important properties are easily calculable. To derive the formula of altitude of an equilateral triangle, two different methods can be used. The. Equilateral Triangle Altitude Proof.
From www.youtube.com
Proof The Equilateral Triangle Theorem YouTube Equilateral Triangle Altitude Proof For any point p within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle. Learn formulas of area, perimeter and. An equilateral triangle is a triangle with all three equal sides and each angle measures up to 60 degrees. It is interesting to note that the altitude of an. Equilateral Triangle Altitude Proof.
From favpng.com
Equilateral Triangle Geometry Altitude, PNG, 1199x968px, Triangle Equilateral Triangle Altitude Proof An equilateral triangle is a triangle with all three equal sides and each angle measures up to 60 degrees. It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle. The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side.. Equilateral Triangle Altitude Proof.
From www.gauthmath.com
Solved An equilateral triangle has a side length of 10 inches. Find Equilateral Triangle Altitude Proof The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side. It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle. To derive the formula of altitude of an equilateral triangle, two different methods can be used. An equilateral triangle. Equilateral Triangle Altitude Proof.