Differential Margin Formula . Using differential analysis, find out the increase in profit if (a) units sold increase by 15%, (b) units sold increase by 10% and variable. Given the function \(z = f\left( {x,y} \right)\) the differential \(dz\) or \(df\) is given by, \[dz = {f_x}\,dx +. Through the lens of economics, we examine how the derivative can be used as a tool to understand marginal cost. The derivative of a constant is zero. We'll use a factory scenario to. The differential [latex]dy=f^{\prime}(a) \, dx[/latex] is used to approximate the actual change in [latex]y[/latex] if [latex]x[/latex] increases from [latex]a[/latex]. The total differential gives a good method of approximating f at nearby points. \[dv = 4\pi {r^2}dr\] now compute \(dv\). So, first get the formula for the differential. See the proof of various derivative formulas section of the extras chapter to see the proof of. Given that f(2, − 3) = 6, fx(2, − 3) = 1.3 and fy(2, − 3) =. \[\delta v \approx dv = 4\pi {\left( {45}.
from www.educba.com
We'll use a factory scenario to. Using differential analysis, find out the increase in profit if (a) units sold increase by 15%, (b) units sold increase by 10% and variable. Given that f(2, − 3) = 6, fx(2, − 3) = 1.3 and fy(2, − 3) =. Given the function \(z = f\left( {x,y} \right)\) the differential \(dz\) or \(df\) is given by, \[dz = {f_x}\,dx +. The total differential gives a good method of approximating f at nearby points. \[\delta v \approx dv = 4\pi {\left( {45}. See the proof of various derivative formulas section of the extras chapter to see the proof of. So, first get the formula for the differential. Through the lens of economics, we examine how the derivative can be used as a tool to understand marginal cost. The derivative of a constant is zero.
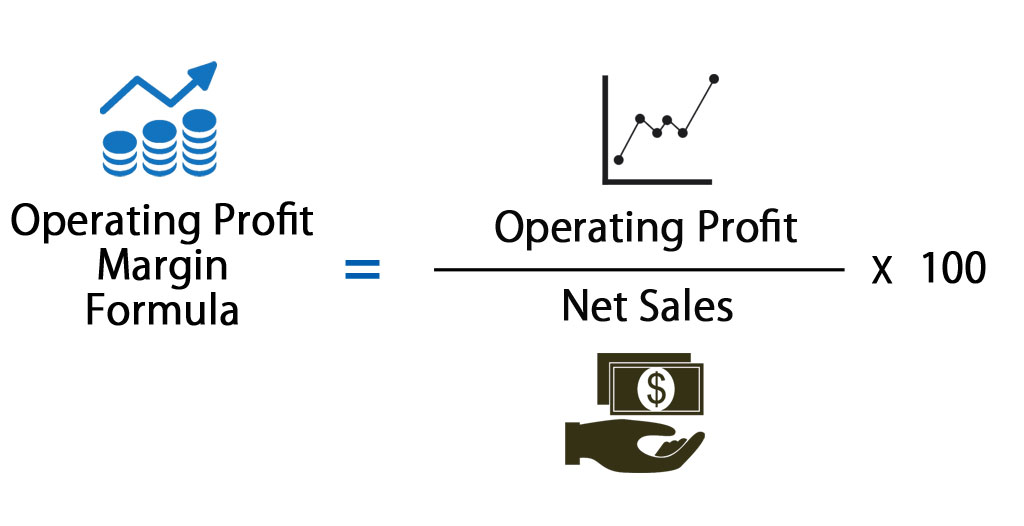
Operating Profit Margin Formula Calculator (Excel template)
Differential Margin Formula \[dv = 4\pi {r^2}dr\] now compute \(dv\). We'll use a factory scenario to. Using differential analysis, find out the increase in profit if (a) units sold increase by 15%, (b) units sold increase by 10% and variable. See the proof of various derivative formulas section of the extras chapter to see the proof of. \[dv = 4\pi {r^2}dr\] now compute \(dv\). The differential [latex]dy=f^{\prime}(a) \, dx[/latex] is used to approximate the actual change in [latex]y[/latex] if [latex]x[/latex] increases from [latex]a[/latex]. The total differential gives a good method of approximating f at nearby points. The derivative of a constant is zero. So, first get the formula for the differential. Given the function \(z = f\left( {x,y} \right)\) the differential \(dz\) or \(df\) is given by, \[dz = {f_x}\,dx +. Through the lens of economics, we examine how the derivative can be used as a tool to understand marginal cost. \[\delta v \approx dv = 4\pi {\left( {45}. Given that f(2, − 3) = 6, fx(2, − 3) = 1.3 and fy(2, − 3) =.
From wise.com
Operating Profit Margin Definition, Formula and Calculation Wise Differential Margin Formula The total differential gives a good method of approximating f at nearby points. So, first get the formula for the differential. The derivative of a constant is zero. Given the function \(z = f\left( {x,y} \right)\) the differential \(dz\) or \(df\) is given by, \[dz = {f_x}\,dx +. Using differential analysis, find out the increase in profit if (a) units. Differential Margin Formula.
From www.wikihow.com
4 Ways to Solve Differential Equations wikiHow Differential Margin Formula Given that f(2, − 3) = 6, fx(2, − 3) = 1.3 and fy(2, − 3) =. Using differential analysis, find out the increase in profit if (a) units sold increase by 15%, (b) units sold increase by 10% and variable. We'll use a factory scenario to. So, first get the formula for the differential. Given the function \(z =. Differential Margin Formula.
From www.wikihow.com
How to Calculate Operating Margin The Formula & How to Use It Differential Margin Formula Through the lens of economics, we examine how the derivative can be used as a tool to understand marginal cost. \[dv = 4\pi {r^2}dr\] now compute \(dv\). Given the function \(z = f\left( {x,y} \right)\) the differential \(dz\) or \(df\) is given by, \[dz = {f_x}\,dx +. We'll use a factory scenario to. The derivative of a constant is zero.. Differential Margin Formula.
From www.investopedia.com
Profit Margin Formula Uses & How to Calculate Differential Margin Formula The total differential gives a good method of approximating f at nearby points. The differential [latex]dy=f^{\prime}(a) \, dx[/latex] is used to approximate the actual change in [latex]y[/latex] if [latex]x[/latex] increases from [latex]a[/latex]. We'll use a factory scenario to. See the proof of various derivative formulas section of the extras chapter to see the proof of. So, first get the formula. Differential Margin Formula.
From www.zendesk.com.br
Profit margin calculator + guide Zendesk Differential Margin Formula \[dv = 4\pi {r^2}dr\] now compute \(dv\). See the proof of various derivative formulas section of the extras chapter to see the proof of. Using differential analysis, find out the increase in profit if (a) units sold increase by 15%, (b) units sold increase by 10% and variable. \[\delta v \approx dv = 4\pi {\left( {45}. We'll use a factory. Differential Margin Formula.
From www.chegg.com
Solved The following single stage differential amplifier Differential Margin Formula The derivative of a constant is zero. Given that f(2, − 3) = 6, fx(2, − 3) = 1.3 and fy(2, − 3) =. The differential [latex]dy=f^{\prime}(a) \, dx[/latex] is used to approximate the actual change in [latex]y[/latex] if [latex]x[/latex] increases from [latex]a[/latex]. We'll use a factory scenario to. So, first get the formula for the differential. \[dv = 4\pi. Differential Margin Formula.
From www.slideserve.com
PPT Maxwell’s Equations Differential and Integral Forms PowerPoint Differential Margin Formula \[dv = 4\pi {r^2}dr\] now compute \(dv\). So, first get the formula for the differential. See the proof of various derivative formulas section of the extras chapter to see the proof of. The derivative of a constant is zero. \[\delta v \approx dv = 4\pi {\left( {45}. The differential [latex]dy=f^{\prime}(a) \, dx[/latex] is used to approximate the actual change in. Differential Margin Formula.
From www.upflip.com
How to Calculate Profit Margins (and Improve Profitability) UpFlip Differential Margin Formula The total differential gives a good method of approximating f at nearby points. \[dv = 4\pi {r^2}dr\] now compute \(dv\). The derivative of a constant is zero. The differential [latex]dy=f^{\prime}(a) \, dx[/latex] is used to approximate the actual change in [latex]y[/latex] if [latex]x[/latex] increases from [latex]a[/latex]. \[\delta v \approx dv = 4\pi {\left( {45}. Given that f(2, − 3) =. Differential Margin Formula.
From www.youtube.com
Explanation of Phase Margin with MATLAB Control Engineering Tutorial Differential Margin Formula \[dv = 4\pi {r^2}dr\] now compute \(dv\). We'll use a factory scenario to. The derivative of a constant is zero. The differential [latex]dy=f^{\prime}(a) \, dx[/latex] is used to approximate the actual change in [latex]y[/latex] if [latex]x[/latex] increases from [latex]a[/latex]. Using differential analysis, find out the increase in profit if (a) units sold increase by 15%, (b) units sold increase by. Differential Margin Formula.
From www.educba.com
Profit Margin Formula Calculator (Examples with Excel Template) Differential Margin Formula Through the lens of economics, we examine how the derivative can be used as a tool to understand marginal cost. We'll use a factory scenario to. See the proof of various derivative formulas section of the extras chapter to see the proof of. \[dv = 4\pi {r^2}dr\] now compute \(dv\). So, first get the formula for the differential. The total. Differential Margin Formula.
From teafmilani.blogspot.com
Actual margin formula TeafMilani Differential Margin Formula See the proof of various derivative formulas section of the extras chapter to see the proof of. The total differential gives a good method of approximating f at nearby points. \[\delta v \approx dv = 4\pi {\left( {45}. The derivative of a constant is zero. The differential [latex]dy=f^{\prime}(a) \, dx[/latex] is used to approximate the actual change in [latex]y[/latex] if. Differential Margin Formula.
From queleparece.com
Margin vs. Markup Which Formula is Best For Your Business? (2023) Differential Margin Formula Using differential analysis, find out the increase in profit if (a) units sold increase by 15%, (b) units sold increase by 10% and variable. The total differential gives a good method of approximating f at nearby points. Through the lens of economics, we examine how the derivative can be used as a tool to understand marginal cost. Given the function. Differential Margin Formula.
From www.wallstreetmojo.com
Operating Profit Margin (Meaning, Formula) How to Calculate? Differential Margin Formula The total differential gives a good method of approximating f at nearby points. We'll use a factory scenario to. \[\delta v \approx dv = 4\pi {\left( {45}. \[dv = 4\pi {r^2}dr\] now compute \(dv\). See the proof of various derivative formulas section of the extras chapter to see the proof of. Through the lens of economics, we examine how the. Differential Margin Formula.
From www.youtube.com
Lec 02 formulation of differential equation, formation of ordinary Differential Margin Formula Given that f(2, − 3) = 6, fx(2, − 3) = 1.3 and fy(2, − 3) =. Through the lens of economics, we examine how the derivative can be used as a tool to understand marginal cost. The total differential gives a good method of approximating f at nearby points. The derivative of a constant is zero. Using differential analysis,. Differential Margin Formula.
From www.slideserve.com
PPT Feedback Amplifier Stability PowerPoint Presentation, free Differential Margin Formula The total differential gives a good method of approximating f at nearby points. We'll use a factory scenario to. So, first get the formula for the differential. The derivative of a constant is zero. See the proof of various derivative formulas section of the extras chapter to see the proof of. Given that f(2, − 3) = 6, fx(2, −. Differential Margin Formula.
From www.flexiprep.com
Mathematics Class 12 NCERT Solutions Chapter 9 Differential Equations Differential Margin Formula Through the lens of economics, we examine how the derivative can be used as a tool to understand marginal cost. See the proof of various derivative formulas section of the extras chapter to see the proof of. The total differential gives a good method of approximating f at nearby points. The differential [latex]dy=f^{\prime}(a) \, dx[/latex] is used to approximate the. Differential Margin Formula.
From www.slideserve.com
PPT Stochastic Differential Equations PowerPoint Presentation, free Differential Margin Formula Using differential analysis, find out the increase in profit if (a) units sold increase by 15%, (b) units sold increase by 10% and variable. Given that f(2, − 3) = 6, fx(2, − 3) = 1.3 and fy(2, − 3) =. Through the lens of economics, we examine how the derivative can be used as a tool to understand marginal. Differential Margin Formula.
From exyehdoxe.blob.core.windows.net
Explain Gross Profit Margin at Ollie Teeter blog Differential Margin Formula Using differential analysis, find out the increase in profit if (a) units sold increase by 15%, (b) units sold increase by 10% and variable. The differential [latex]dy=f^{\prime}(a) \, dx[/latex] is used to approximate the actual change in [latex]y[/latex] if [latex]x[/latex] increases from [latex]a[/latex]. Given that f(2, − 3) = 6, fx(2, − 3) = 1.3 and fy(2, − 3) =.. Differential Margin Formula.
From www.chegg.com
Solved The governing differential equation for the Differential Margin Formula The differential [latex]dy=f^{\prime}(a) \, dx[/latex] is used to approximate the actual change in [latex]y[/latex] if [latex]x[/latex] increases from [latex]a[/latex]. See the proof of various derivative formulas section of the extras chapter to see the proof of. So, first get the formula for the differential. \[dv = 4\pi {r^2}dr\] now compute \(dv\). Given the function \(z = f\left( {x,y} \right)\) the. Differential Margin Formula.
From www.chegg.com
Solved The partial differential equation for twodimensional Differential Margin Formula See the proof of various derivative formulas section of the extras chapter to see the proof of. The total differential gives a good method of approximating f at nearby points. Given the function \(z = f\left( {x,y} \right)\) the differential \(dz\) or \(df\) is given by, \[dz = {f_x}\,dx +. Using differential analysis, find out the increase in profit if. Differential Margin Formula.
From www.youtube.com
Laplace's Equation Partial Differential Equations with an Example YouTube Differential Margin Formula \[dv = 4\pi {r^2}dr\] now compute \(dv\). The derivative of a constant is zero. We'll use a factory scenario to. See the proof of various derivative formulas section of the extras chapter to see the proof of. Using differential analysis, find out the increase in profit if (a) units sold increase by 15%, (b) units sold increase by 10% and. Differential Margin Formula.
From www.coursehero.com
[Solved] Form the partial differential equation by eliminating the Differential Margin Formula Through the lens of economics, we examine how the derivative can be used as a tool to understand marginal cost. \[\delta v \approx dv = 4\pi {\left( {45}. Using differential analysis, find out the increase in profit if (a) units sold increase by 15%, (b) units sold increase by 10% and variable. Given that f(2, − 3) = 6, fx(2,. Differential Margin Formula.
From www.cuemath.com
Differential Equations Definition, Formula, Types, Examples Differential Margin Formula The total differential gives a good method of approximating f at nearby points. Using differential analysis, find out the increase in profit if (a) units sold increase by 15%, (b) units sold increase by 10% and variable. \[\delta v \approx dv = 4\pi {\left( {45}. See the proof of various derivative formulas section of the extras chapter to see the. Differential Margin Formula.
From roseannsaria.blogspot.com
Margin required calculator RoseannSaria Differential Margin Formula So, first get the formula for the differential. \[\delta v \approx dv = 4\pi {\left( {45}. The total differential gives a good method of approximating f at nearby points. The derivative of a constant is zero. Given that f(2, − 3) = 6, fx(2, − 3) = 1.3 and fy(2, − 3) =. The differential [latex]dy=f^{\prime}(a) \, dx[/latex] is used. Differential Margin Formula.
From www.wallstreetprep.com
What is FCF Margin? Formula + Calculator Differential Margin Formula So, first get the formula for the differential. Given that f(2, − 3) = 6, fx(2, − 3) = 1.3 and fy(2, − 3) =. Through the lens of economics, we examine how the derivative can be used as a tool to understand marginal cost. Given the function \(z = f\left( {x,y} \right)\) the differential \(dz\) or \(df\) is given. Differential Margin Formula.
From www.thestreet.com
What Is Profit Margin? Definition, Types, How to Calculate, Example Differential Margin Formula See the proof of various derivative formulas section of the extras chapter to see the proof of. The total differential gives a good method of approximating f at nearby points. We'll use a factory scenario to. Given the function \(z = f\left( {x,y} \right)\) the differential \(dz\) or \(df\) is given by, \[dz = {f_x}\,dx +. So, first get the. Differential Margin Formula.
From www.slideserve.com
PPT Chapter 2 SecondOrder Differential Equations PowerPoint Differential Margin Formula The total differential gives a good method of approximating f at nearby points. \[dv = 4\pi {r^2}dr\] now compute \(dv\). See the proof of various derivative formulas section of the extras chapter to see the proof of. Through the lens of economics, we examine how the derivative can be used as a tool to understand marginal cost. Using differential analysis,. Differential Margin Formula.
From www.upflip.com
How to Calculate Profit Margins (and Improve Profitability) UpFlip Differential Margin Formula See the proof of various derivative formulas section of the extras chapter to see the proof of. The differential [latex]dy=f^{\prime}(a) \, dx[/latex] is used to approximate the actual change in [latex]y[/latex] if [latex]x[/latex] increases from [latex]a[/latex]. Given that f(2, − 3) = 6, fx(2, − 3) = 1.3 and fy(2, − 3) =. The derivative of a constant is zero.. Differential Margin Formula.
From www.python-unleashed.com
SVM Margin Formula Derivation Differential Margin Formula So, first get the formula for the differential. Through the lens of economics, we examine how the derivative can be used as a tool to understand marginal cost. The differential [latex]dy=f^{\prime}(a) \, dx[/latex] is used to approximate the actual change in [latex]y[/latex] if [latex]x[/latex] increases from [latex]a[/latex]. See the proof of various derivative formulas section of the extras chapter to. Differential Margin Formula.
From www.nagwa.com
Question Video Solving a Separable FirstOrder Differential Equation Differential Margin Formula We'll use a factory scenario to. \[\delta v \approx dv = 4\pi {\left( {45}. See the proof of various derivative formulas section of the extras chapter to see the proof of. The total differential gives a good method of approximating f at nearby points. So, first get the formula for the differential. Given that f(2, − 3) = 6, fx(2,. Differential Margin Formula.
From thecuriouss.com
what is profit margin their types and calculation Differential Margin Formula We'll use a factory scenario to. \[dv = 4\pi {r^2}dr\] now compute \(dv\). \[\delta v \approx dv = 4\pi {\left( {45}. Using differential analysis, find out the increase in profit if (a) units sold increase by 15%, (b) units sold increase by 10% and variable. The derivative of a constant is zero. Given that f(2, − 3) = 6, fx(2,. Differential Margin Formula.
From www.toppr.com
Obtain the differential equation by eliminating the arbitrary constants Differential Margin Formula The total differential gives a good method of approximating f at nearby points. So, first get the formula for the differential. Given the function \(z = f\left( {x,y} \right)\) the differential \(dz\) or \(df\) is given by, \[dz = {f_x}\,dx +. Through the lens of economics, we examine how the derivative can be used as a tool to understand marginal. Differential Margin Formula.
From caronmaddisyn.blogspot.com
Front margin calculation CarynMadeline Differential Margin Formula \[\delta v \approx dv = 4\pi {\left( {45}. Through the lens of economics, we examine how the derivative can be used as a tool to understand marginal cost. Given that f(2, − 3) = 6, fx(2, − 3) = 1.3 and fy(2, − 3) =. So, first get the formula for the differential. Given the function \(z = f\left( {x,y}. Differential Margin Formula.
From www.slideserve.com
PPT Feedback Amplifier Stability PowerPoint Presentation, free Differential Margin Formula Through the lens of economics, we examine how the derivative can be used as a tool to understand marginal cost. The derivative of a constant is zero. \[dv = 4\pi {r^2}dr\] now compute \(dv\). The differential [latex]dy=f^{\prime}(a) \, dx[/latex] is used to approximate the actual change in [latex]y[/latex] if [latex]x[/latex] increases from [latex]a[/latex]. \[\delta v \approx dv = 4\pi {\left(. Differential Margin Formula.
From www.educba.com
Operating Profit Margin Formula Calculator (Excel template) Differential Margin Formula So, first get the formula for the differential. The differential [latex]dy=f^{\prime}(a) \, dx[/latex] is used to approximate the actual change in [latex]y[/latex] if [latex]x[/latex] increases from [latex]a[/latex]. See the proof of various derivative formulas section of the extras chapter to see the proof of. Given that f(2, − 3) = 6, fx(2, − 3) = 1.3 and fy(2, − 3). Differential Margin Formula.