Triangular Numbers Formula C++ . $nth$ triangular number is the sum of $n$ consecutive natural numbers from starting which is simply $n(n+1)/2$. a triangular number or triangle number counts objects arranged in an equilateral triangle, as in the diagram on. we were asked to make a triangular number pattern in c++ with minimum loops: solving for m using the quadratic formula: So n is triangular if and only if 8n+1 is a. in this problem, we are given a number n which is given the n of elements of the series 1, 3, 6, 10. a triangular number is a number that can be expressed as the sum of the first n consecutive positive integers. a triangular number or triangle number is the sum of the natural numbers up to a certain value. triangular numbers are a sequence of numbers that represent the number of dots that can form an equilateral triangle.
from findthefactors.com
So n is triangular if and only if 8n+1 is a. a triangular number or triangle number counts objects arranged in an equilateral triangle, as in the diagram on. solving for m using the quadratic formula: we were asked to make a triangular number pattern in c++ with minimum loops: a triangular number or triangle number is the sum of the natural numbers up to a certain value. triangular numbers are a sequence of numbers that represent the number of dots that can form an equilateral triangle. a triangular number is a number that can be expressed as the sum of the first n consecutive positive integers. in this problem, we are given a number n which is given the n of elements of the series 1, 3, 6, 10. $nth$ triangular number is the sum of $n$ consecutive natural numbers from starting which is simply $n(n+1)/2$.
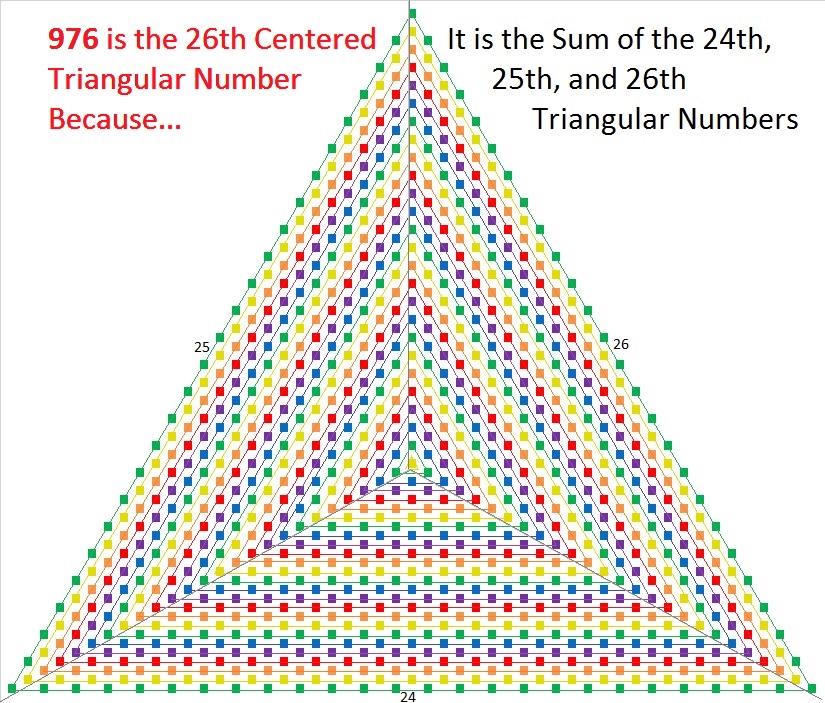
What Kind of Shape is 976 in? Find the Factors
Triangular Numbers Formula C++ a triangular number or triangle number counts objects arranged in an equilateral triangle, as in the diagram on. $nth$ triangular number is the sum of $n$ consecutive natural numbers from starting which is simply $n(n+1)/2$. solving for m using the quadratic formula: a triangular number or triangle number is the sum of the natural numbers up to a certain value. So n is triangular if and only if 8n+1 is a. in this problem, we are given a number n which is given the n of elements of the series 1, 3, 6, 10. triangular numbers are a sequence of numbers that represent the number of dots that can form an equilateral triangle. a triangular number is a number that can be expressed as the sum of the first n consecutive positive integers. a triangular number or triangle number counts objects arranged in an equilateral triangle, as in the diagram on. we were asked to make a triangular number pattern in c++ with minimum loops:
From www.pinterest.com
Pascal's triangle triangular numbers and binomial coefficients Triangular Numbers Formula C++ So n is triangular if and only if 8n+1 is a. a triangular number or triangle number counts objects arranged in an equilateral triangle, as in the diagram on. a triangular number or triangle number is the sum of the natural numbers up to a certain value. $nth$ triangular number is the sum of $n$ consecutive natural. Triangular Numbers Formula C++.
From www.youtube.com
Sum of Triangular Numbers I (visual proof) YouTube Triangular Numbers Formula C++ $nth$ triangular number is the sum of $n$ consecutive natural numbers from starting which is simply $n(n+1)/2$. triangular numbers are a sequence of numbers that represent the number of dots that can form an equilateral triangle. a triangular number or triangle number is the sum of the natural numbers up to a certain value. in this. Triangular Numbers Formula C++.
From thirdspacelearning.com
Triangular Numbers GCSE Maths Steps, Examples & Worksheet Triangular Numbers Formula C++ a triangular number or triangle number is the sum of the natural numbers up to a certain value. in this problem, we are given a number n which is given the n of elements of the series 1, 3, 6, 10. we were asked to make a triangular number pattern in c++ with minimum loops: $nth$. Triangular Numbers Formula C++.
From www.media4math.com
DefinitionSequences and Series ConceptsTriangular Numbers Media4Math Triangular Numbers Formula C++ in this problem, we are given a number n which is given the n of elements of the series 1, 3, 6, 10. $nth$ triangular number is the sum of $n$ consecutive natural numbers from starting which is simply $n(n+1)/2$. solving for m using the quadratic formula: triangular numbers are a sequence of numbers that represent. Triangular Numbers Formula C++.
From www.youtube.com
[ANT08b] Square triangular numbers YouTube Triangular Numbers Formula C++ solving for m using the quadratic formula: a triangular number or triangle number counts objects arranged in an equilateral triangle, as in the diagram on. a triangular number is a number that can be expressed as the sum of the first n consecutive positive integers. $nth$ triangular number is the sum of $n$ consecutive natural numbers. Triangular Numbers Formula C++.
From creationpie.com
Triangular numbers Triangular Numbers Formula C++ a triangular number or triangle number is the sum of the natural numbers up to a certain value. in this problem, we are given a number n which is given the n of elements of the series 1, 3, 6, 10. a triangular number or triangle number counts objects arranged in an equilateral triangle, as in the. Triangular Numbers Formula C++.
From www.shutterstock.com
fórmula de números triangulares en matemática vector de stock (libre Triangular Numbers Formula C++ we were asked to make a triangular number pattern in c++ with minimum loops: a triangular number or triangle number counts objects arranged in an equilateral triangle, as in the diagram on. a triangular number is a number that can be expressed as the sum of the first n consecutive positive integers. in this problem, we. Triangular Numbers Formula C++.
From barcelonageeks.com
Programa C/C++ para número triangular de cerillas Barcelona Geeks Triangular Numbers Formula C++ a triangular number is a number that can be expressed as the sum of the first n consecutive positive integers. $nth$ triangular number is the sum of $n$ consecutive natural numbers from starting which is simply $n(n+1)/2$. So n is triangular if and only if 8n+1 is a. we were asked to make a triangular number pattern. Triangular Numbers Formula C++.
From giosyymnk.blob.core.windows.net
Triangular Number Formula Explanation at Amber Giroux blog Triangular Numbers Formula C++ So n is triangular if and only if 8n+1 is a. $nth$ triangular number is the sum of $n$ consecutive natural numbers from starting which is simply $n(n+1)/2$. we were asked to make a triangular number pattern in c++ with minimum loops: triangular numbers are a sequence of numbers that represent the number of dots that can. Triangular Numbers Formula C++.
From www.numerade.com
SOLVEDGeometry The triangular numbers form a sequence. The diagram Triangular Numbers Formula C++ $nth$ triangular number is the sum of $n$ consecutive natural numbers from starting which is simply $n(n+1)/2$. we were asked to make a triangular number pattern in c++ with minimum loops: triangular numbers are a sequence of numbers that represent the number of dots that can form an equilateral triangle. a triangular number is a number. Triangular Numbers Formula C++.
From www.pdffiller.com
Fillable Online Triangular Numbers Sequence List and Formula Fax Triangular Numbers Formula C++ in this problem, we are given a number n which is given the n of elements of the series 1, 3, 6, 10. we were asked to make a triangular number pattern in c++ with minimum loops: $nth$ triangular number is the sum of $n$ consecutive natural numbers from starting which is simply $n(n+1)/2$. a triangular. Triangular Numbers Formula C++.
From findthefactors.com
What Kind of Shape is 976 in? Find the Factors Triangular Numbers Formula C++ So n is triangular if and only if 8n+1 is a. a triangular number or triangle number is the sum of the natural numbers up to a certain value. triangular numbers are a sequence of numbers that represent the number of dots that can form an equilateral triangle. a triangular number or triangle number counts objects arranged. Triangular Numbers Formula C++.
From owlcation.com
What Are Triangular Numbers? Owlcation Triangular Numbers Formula C++ So n is triangular if and only if 8n+1 is a. $nth$ triangular number is the sum of $n$ consecutive natural numbers from starting which is simply $n(n+1)/2$. solving for m using the quadratic formula: triangular numbers are a sequence of numbers that represent the number of dots that can form an equilateral triangle. a triangular. Triangular Numbers Formula C++.
From giorvzxrs.blob.core.windows.net
Square And Triangular Numbers Worksheets at Venita Hicks blog Triangular Numbers Formula C++ we were asked to make a triangular number pattern in c++ with minimum loops: So n is triangular if and only if 8n+1 is a. a triangular number or triangle number counts objects arranged in an equilateral triangle, as in the diagram on. a triangular number is a number that can be expressed as the sum of. Triangular Numbers Formula C++.
From www.youtube.com
Tetrahedral Numbers Sum of 'n' Consecutive Triangular Numbers Proof Triangular Numbers Formula C++ a triangular number is a number that can be expressed as the sum of the first n consecutive positive integers. a triangular number or triangle number is the sum of the natural numbers up to a certain value. triangular numbers are a sequence of numbers that represent the number of dots that can form an equilateral triangle.. Triangular Numbers Formula C++.
From shyamsundergupta.net
Fascinating Triangular Numbers By Shyam Sunder Gupta Triangular Numbers Formula C++ $nth$ triangular number is the sum of $n$ consecutive natural numbers from starting which is simply $n(n+1)/2$. a triangular number or triangle number counts objects arranged in an equilateral triangle, as in the diagram on. we were asked to make a triangular number pattern in c++ with minimum loops: in this problem, we are given a. Triangular Numbers Formula C++.
From www.chegg.com
Solved Triangular number Series A triangle number counts Triangular Numbers Formula C++ in this problem, we are given a number n which is given the n of elements of the series 1, 3, 6, 10. solving for m using the quadratic formula: a triangular number or triangle number counts objects arranged in an equilateral triangle, as in the diagram on. we were asked to make a triangular number. Triangular Numbers Formula C++.
From www.shutterstock.com
Triangular Numbers Formula Mathematic Stock Vector (Royalty Free Triangular Numbers Formula C++ triangular numbers are a sequence of numbers that represent the number of dots that can form an equilateral triangle. a triangular number is a number that can be expressed as the sum of the first n consecutive positive integers. a triangular number or triangle number counts objects arranged in an equilateral triangle, as in the diagram on.. Triangular Numbers Formula C++.
From www.youtube.com
Triangle Counting Trick by Formula│Triangle Reasoning Shortcut Trick Triangular Numbers Formula C++ So n is triangular if and only if 8n+1 is a. a triangular number is a number that can be expressed as the sum of the first n consecutive positive integers. a triangular number or triangle number is the sum of the natural numbers up to a certain value. a triangular number or triangle number counts objects. Triangular Numbers Formula C++.
From ontargetresources.co.uk
Transfer Test Tips Triangular Numbers On Target Resources Triangular Numbers Formula C++ a triangular number or triangle number counts objects arranged in an equilateral triangle, as in the diagram on. triangular numbers are a sequence of numbers that represent the number of dots that can form an equilateral triangle. So n is triangular if and only if 8n+1 is a. $nth$ triangular number is the sum of $n$ consecutive. Triangular Numbers Formula C++.
From www.youtube.com
Triangular Numbers YouTube Triangular Numbers Formula C++ we were asked to make a triangular number pattern in c++ with minimum loops: in this problem, we are given a number n which is given the n of elements of the series 1, 3, 6, 10. So n is triangular if and only if 8n+1 is a. a triangular number is a number that can be. Triangular Numbers Formula C++.
From www.youtube.com
What Are the Triangular Numbers? Popular Mathematical Sequences YouTube Triangular Numbers Formula C++ we were asked to make a triangular number pattern in c++ with minimum loops: a triangular number or triangle number counts objects arranged in an equilateral triangle, as in the diagram on. a triangular number is a number that can be expressed as the sum of the first n consecutive positive integers. So n is triangular if. Triangular Numbers Formula C++.
From thirdspacelearning.com
Triangular Numbers GCSE Maths Steps, Examples & Worksheet Triangular Numbers Formula C++ $nth$ triangular number is the sum of $n$ consecutive natural numbers from starting which is simply $n(n+1)/2$. in this problem, we are given a number n which is given the n of elements of the series 1, 3, 6, 10. we were asked to make a triangular number pattern in c++ with minimum loops: a triangular. Triangular Numbers Formula C++.
From aperiodical.com
Sequences in the triangle and the fourth dimension The Aperiodical Triangular Numbers Formula C++ triangular numbers are a sequence of numbers that represent the number of dots that can form an equilateral triangle. in this problem, we are given a number n which is given the n of elements of the series 1, 3, 6, 10. a triangular number is a number that can be expressed as the sum of the. Triangular Numbers Formula C++.
From byjus.com
Triangular Numbers Sequence List Of Triangular Numbers Formula to Triangular Numbers Formula C++ we were asked to make a triangular number pattern in c++ with minimum loops: $nth$ triangular number is the sum of $n$ consecutive natural numbers from starting which is simply $n(n+1)/2$. triangular numbers are a sequence of numbers that represent the number of dots that can form an equilateral triangle. in this problem, we are given. Triangular Numbers Formula C++.
From giosyymnk.blob.core.windows.net
Triangular Number Formula Explanation at Amber Giroux blog Triangular Numbers Formula C++ $nth$ triangular number is the sum of $n$ consecutive natural numbers from starting which is simply $n(n+1)/2$. So n is triangular if and only if 8n+1 is a. in this problem, we are given a number n which is given the n of elements of the series 1, 3, 6, 10. solving for m using the quadratic. Triangular Numbers Formula C++.
From www.aakash.ac.in
Triangular Numbers in Maths Definition, Types and Importance of Triangular Numbers Formula C++ a triangular number is a number that can be expressed as the sum of the first n consecutive positive integers. we were asked to make a triangular number pattern in c++ with minimum loops: a triangular number or triangle number is the sum of the natural numbers up to a certain value. $nth$ triangular number is. Triangular Numbers Formula C++.
From www.studypool.com
SOLUTION The sequence of triangular numbers formula Studypool Triangular Numbers Formula C++ So n is triangular if and only if 8n+1 is a. we were asked to make a triangular number pattern in c++ with minimum loops: a triangular number or triangle number counts objects arranged in an equilateral triangle, as in the diagram on. a triangular number or triangle number is the sum of the natural numbers up. Triangular Numbers Formula C++.
From robinsnyder.org
Triangular numbers Triangular Numbers Formula C++ a triangular number is a number that can be expressed as the sum of the first n consecutive positive integers. in this problem, we are given a number n which is given the n of elements of the series 1, 3, 6, 10. solving for m using the quadratic formula: So n is triangular if and only. Triangular Numbers Formula C++.
From thirdspacelearning.com
Triangular Numbers GCSE Maths Steps, Examples & Worksheet Triangular Numbers Formula C++ triangular numbers are a sequence of numbers that represent the number of dots that can form an equilateral triangle. in this problem, we are given a number n which is given the n of elements of the series 1, 3, 6, 10. we were asked to make a triangular number pattern in c++ with minimum loops: . Triangular Numbers Formula C++.
From ftp.intelligencetest.com
Number sequences tips Triangular Numbers Formula C++ we were asked to make a triangular number pattern in c++ with minimum loops: solving for m using the quadratic formula: a triangular number is a number that can be expressed as the sum of the first n consecutive positive integers. a triangular number or triangle number is the sum of the natural numbers up to. Triangular Numbers Formula C++.
From nghs12acc.blogspot.com
core pure 3 notes triangular numbers Triangular Numbers Formula C++ we were asked to make a triangular number pattern in c++ with minimum loops: triangular numbers are a sequence of numbers that represent the number of dots that can form an equilateral triangle. $nth$ triangular number is the sum of $n$ consecutive natural numbers from starting which is simply $n(n+1)/2$. solving for m using the quadratic. Triangular Numbers Formula C++.
From www.chegg.com
Solved The nth triangular number T_n is the sum of the first Triangular Numbers Formula C++ triangular numbers are a sequence of numbers that represent the number of dots that can form an equilateral triangle. solving for m using the quadratic formula: a triangular number or triangle number counts objects arranged in an equilateral triangle, as in the diagram on. $nth$ triangular number is the sum of $n$ consecutive natural numbers from. Triangular Numbers Formula C++.
From gbu-taganskij.ru
SOLVED The First Four Triangular Numbers Are Shown Below,, 49 OFF Triangular Numbers Formula C++ we were asked to make a triangular number pattern in c++ with minimum loops: So n is triangular if and only if 8n+1 is a. a triangular number or triangle number is the sum of the natural numbers up to a certain value. a triangular number is a number that can be expressed as the sum of. Triangular Numbers Formula C++.
From www.artofit.org
Triangular numbers Artofit Triangular Numbers Formula C++ a triangular number is a number that can be expressed as the sum of the first n consecutive positive integers. a triangular number or triangle number counts objects arranged in an equilateral triangle, as in the diagram on. a triangular number or triangle number is the sum of the natural numbers up to a certain value. . Triangular Numbers Formula C++.