Inner Product Between Matrices . it's worth noting that, with this definition (see answer by @dietrich burde), the standard inner product of two rectangular real. the inner product of matrices is defined for two matrices a and b of the same size. It takes two inputs from the vector space) which. Given matrices a = [a i j] and b = [b i j], both of size m x. for all \mathbf {x}, so \langle\mathbf {x}, \mathbf {x}\rangle=0 implies \mathbf {x}=\mathbf {0}. Here, rm nis the space. In a vector space, it is a way to multiply vectors. the standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. an inner product is a binary function on a vector space (i.e. A, b = t r (a b ⊺). an inner product is a generalization of the dot product. Hence \langle, \rangle is indeed an inner product, so a is. the standard inner product between matrices is often chosen to be.
from www.youtube.com
the standard inner product between matrices is often chosen to be. the standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. the inner product of matrices is defined for two matrices a and b of the same size. for all \mathbf {x}, so \langle\mathbf {x}, \mathbf {x}\rangle=0 implies \mathbf {x}=\mathbf {0}. Here, rm nis the space. In a vector space, it is a way to multiply vectors. A, b = t r (a b ⊺). Hence \langle, \rangle is indeed an inner product, so a is. an inner product is a generalization of the dot product. an inner product is a binary function on a vector space (i.e.
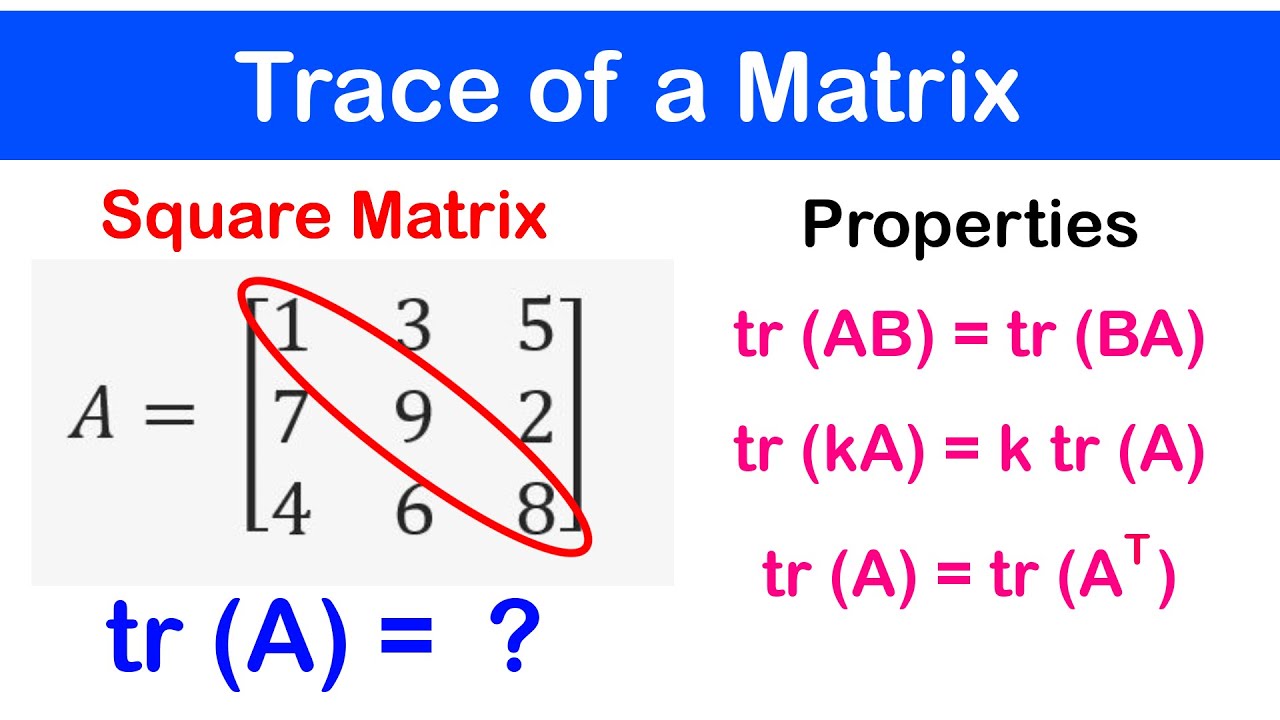
🔷05 Trace of a Matrix Properties of the Trace of a given Matrix
Inner Product Between Matrices A, b = t r (a b ⊺). Here, rm nis the space. an inner product is a binary function on a vector space (i.e. for all \mathbf {x}, so \langle\mathbf {x}, \mathbf {x}\rangle=0 implies \mathbf {x}=\mathbf {0}. an inner product is a generalization of the dot product. the inner product of matrices is defined for two matrices a and b of the same size. In a vector space, it is a way to multiply vectors. It takes two inputs from the vector space) which. it's worth noting that, with this definition (see answer by @dietrich burde), the standard inner product of two rectangular real. A, b = t r (a b ⊺). the standard inner product between matrices is often chosen to be. Given matrices a = [a i j] and b = [b i j], both of size m x. the standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. Hence \langle, \rangle is indeed an inner product, so a is.
From www.slideserve.com
PPT Linear Transformations and Matrices PowerPoint Presentation, free Inner Product Between Matrices the inner product of matrices is defined for two matrices a and b of the same size. It takes two inputs from the vector space) which. the standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. Hence \langle, \rangle is indeed an inner product, so a is.. Inner Product Between Matrices.
From www.slideserve.com
PPT Inverse Kinematics Jacobian Matrix Trajectory Planning PowerPoint Inner Product Between Matrices the inner product of matrices is defined for two matrices a and b of the same size. for all \mathbf {x}, so \langle\mathbf {x}, \mathbf {x}\rangle=0 implies \mathbf {x}=\mathbf {0}. Here, rm nis the space. an inner product is a binary function on a vector space (i.e. it's worth noting that, with this definition (see answer. Inner Product Between Matrices.
From www.youtube.com
Inner Product Spaces YouTube Inner Product Between Matrices for all \mathbf {x}, so \langle\mathbf {x}, \mathbf {x}\rangle=0 implies \mathbf {x}=\mathbf {0}. the standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. Given matrices a = [a i j] and b = [b i j], both of size m x. Here, rm nis the space. . Inner Product Between Matrices.
From crossproductcalculator.org
Dot Product vs Cross Product What's the Difference? Inner Product Between Matrices an inner product is a binary function on a vector space (i.e. for all \mathbf {x}, so \langle\mathbf {x}, \mathbf {x}\rangle=0 implies \mathbf {x}=\mathbf {0}. Hence \langle, \rangle is indeed an inner product, so a is. it's worth noting that, with this definition (see answer by @dietrich burde), the standard inner product of two rectangular real. Given. Inner Product Between Matrices.
From mavink.com
Writing A Matrix In Matlab Inner Product Between Matrices A, b = t r (a b ⊺). the standard inner product between matrices is often chosen to be. the standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. for all \mathbf {x}, so \langle\mathbf {x}, \mathbf {x}\rangle=0 implies \mathbf {x}=\mathbf {0}. Here, rm nis the. Inner Product Between Matrices.
From www.youtube.com
Inner product vs dot product YouTube Inner Product Between Matrices an inner product is a binary function on a vector space (i.e. for all \mathbf {x}, so \langle\mathbf {x}, \mathbf {x}\rangle=0 implies \mathbf {x}=\mathbf {0}. In a vector space, it is a way to multiply vectors. Hence \langle, \rangle is indeed an inner product, so a is. the standard inner product between matrices is hx;yi= tr(xty) =. Inner Product Between Matrices.
From www.slideserve.com
PPT Review of Linear Algebra PowerPoint Presentation, free download Inner Product Between Matrices In a vector space, it is a way to multiply vectors. Hence \langle, \rangle is indeed an inner product, so a is. an inner product is a binary function on a vector space (i.e. the standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. It takes two. Inner Product Between Matrices.
From www.math3ma.com
The Tensor Product, Demystified Inner Product Between Matrices Here, rm nis the space. A, b = t r (a b ⊺). In a vector space, it is a way to multiply vectors. an inner product is a binary function on a vector space (i.e. It takes two inputs from the vector space) which. it's worth noting that, with this definition (see answer by @dietrich burde), the. Inner Product Between Matrices.
From pistexy.blogspot.com
Determinant Of 2X2 Matrix Determinant of 3x3 matrix YouTube The Inner Product Between Matrices the inner product of matrices is defined for two matrices a and b of the same size. It takes two inputs from the vector space) which. the standard inner product between matrices is often chosen to be. A, b = t r (a b ⊺). an inner product is a binary function on a vector space (i.e.. Inner Product Between Matrices.
From www.reddit.com
[Linear algebra] matrix multiplication vs dot product learnmath Inner Product Between Matrices it's worth noting that, with this definition (see answer by @dietrich burde), the standard inner product of two rectangular real. the standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. the inner product of matrices is defined for two matrices a and b of the same. Inner Product Between Matrices.
From ar.inspiredpencil.com
Product Multiplication Inner Product Between Matrices Hence \langle, \rangle is indeed an inner product, so a is. It takes two inputs from the vector space) which. it's worth noting that, with this definition (see answer by @dietrich burde), the standard inner product of two rectangular real. Here, rm nis the space. the standard inner product between matrices is often chosen to be. A, b. Inner Product Between Matrices.
From www.youtube.com
How To Multiply Matrices Quick & Easy! YouTube Inner Product Between Matrices an inner product is a binary function on a vector space (i.e. the standard inner product between matrices is often chosen to be. In a vector space, it is a way to multiply vectors. the inner product of matrices is defined for two matrices a and b of the same size. Hence \langle, \rangle is indeed an. Inner Product Between Matrices.
From debmoran.blogspot.com
Differentiate Between Row Matrix And Column Matrix Deb Moran's Inner Product Between Matrices an inner product is a generalization of the dot product. the standard inner product between matrices is often chosen to be. It takes two inputs from the vector space) which. the inner product of matrices is defined for two matrices a and b of the same size. Here, rm nis the space. Hence \langle, \rangle is indeed. Inner Product Between Matrices.
From www.youtube.com
Matrixvector and Matrixmatrix Multiplication YouTube Inner Product Between Matrices the standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. it's worth noting that, with this definition (see answer by @dietrich burde), the standard inner product of two rectangular real. A, b = t r (a b ⊺). Here, rm nis the space. an inner product. Inner Product Between Matrices.
From math.stackexchange.com
linear algebra Outer product form of the SVD Mathematics Stack Exchange Inner Product Between Matrices Given matrices a = [a i j] and b = [b i j], both of size m x. A, b = t r (a b ⊺). It takes two inputs from the vector space) which. an inner product is a generalization of the dot product. the standard inner product between matrices is hx;yi= tr(xty) = x i x. Inner Product Between Matrices.
From www.slideserve.com
PPT Lecture 9 Symmetric Matrices Subspaces and Nullspaces PowerPoint Inner Product Between Matrices it's worth noting that, with this definition (see answer by @dietrich burde), the standard inner product of two rectangular real. an inner product is a generalization of the dot product. Here, rm nis the space. In a vector space, it is a way to multiply vectors. the inner product of matrices is defined for two matrices a. Inner Product Between Matrices.
From www.math3ma.com
The Tensor Product, Demystified Inner Product Between Matrices A, b = t r (a b ⊺). it's worth noting that, with this definition (see answer by @dietrich burde), the standard inner product of two rectangular real. In a vector space, it is a way to multiply vectors. an inner product is a binary function on a vector space (i.e. an inner product is a generalization. Inner Product Between Matrices.
From www.youtube.com
🔷05 Trace of a Matrix Properties of the Trace of a given Matrix Inner Product Between Matrices an inner product is a binary function on a vector space (i.e. it's worth noting that, with this definition (see answer by @dietrich burde), the standard inner product of two rectangular real. It takes two inputs from the vector space) which. the standard inner product between matrices is often chosen to be. Given matrices a = [a. Inner Product Between Matrices.
From www.youtube.com
General Inner Products in ℝⁿ. Matrix Representation YouTube Inner Product Between Matrices for all \mathbf {x}, so \langle\mathbf {x}, \mathbf {x}\rangle=0 implies \mathbf {x}=\mathbf {0}. the inner product of matrices is defined for two matrices a and b of the same size. Hence \langle, \rangle is indeed an inner product, so a is. In a vector space, it is a way to multiply vectors. A, b = t r (a. Inner Product Between Matrices.
From chem.libretexts.org
15.3 Matrix Multiplication Chemistry LibreTexts Inner Product Between Matrices In a vector space, it is a way to multiply vectors. for all \mathbf {x}, so \langle\mathbf {x}, \mathbf {x}\rangle=0 implies \mathbf {x}=\mathbf {0}. the standard inner product between matrices is often chosen to be. the standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. . Inner Product Between Matrices.
From www.slideserve.com
PPT Elementary Linear Algebra Anton & Rorres, 9 th Edition PowerPoint Inner Product Between Matrices In a vector space, it is a way to multiply vectors. It takes two inputs from the vector space) which. A, b = t r (a b ⊺). Here, rm nis the space. the inner product of matrices is defined for two matrices a and b of the same size. for all \mathbf {x}, so \langle\mathbf {x}, \mathbf. Inner Product Between Matrices.
From vsbattles.com
Animator vs. Animation Tier 1 upgrade VS Battles Wiki Forum Inner Product Between Matrices an inner product is a binary function on a vector space (i.e. for all \mathbf {x}, so \langle\mathbf {x}, \mathbf {x}\rangle=0 implies \mathbf {x}=\mathbf {0}. it's worth noting that, with this definition (see answer by @dietrich burde), the standard inner product of two rectangular real. Given matrices a = [a i j] and b = [b i. Inner Product Between Matrices.
From www.youtube.com
Outer Products YouTube Inner Product Between Matrices Here, rm nis the space. the standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. an inner product is a binary function on a vector space (i.e. an inner product is a generalization of the dot product. for all \mathbf {x}, so \langle\mathbf {x}, \mathbf. Inner Product Between Matrices.
From www.youtube.com
Outer product vs inner product, and matrix representation of operator Inner Product Between Matrices the standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. Given matrices a = [a i j] and b = [b i j], both of size m x. the standard inner product between matrices is often chosen to be. It takes two inputs from the vector space). Inner Product Between Matrices.
From www.youtube.com
44 The Kronecker Product of two matrices an introduction YouTube Inner Product Between Matrices the inner product of matrices is defined for two matrices a and b of the same size. It takes two inputs from the vector space) which. an inner product is a binary function on a vector space (i.e. the standard inner product between matrices is often chosen to be. it's worth noting that, with this definition. Inner Product Between Matrices.
From datahacker.rs
Inner (Dot) product of two Vectors. Applications in Machine Learning Inner Product Between Matrices A, b = t r (a b ⊺). Here, rm nis the space. the standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. the inner product of matrices is defined for two matrices a and b of the same size. Hence \langle, \rangle is indeed an inner. Inner Product Between Matrices.
From blog.allenai.org
The lure of the outer product. Bilinear pooling and its approximations Inner Product Between Matrices the standard inner product between matrices is often chosen to be. In a vector space, it is a way to multiply vectors. the inner product of matrices is defined for two matrices a and b of the same size. Hence \langle, \rangle is indeed an inner product, so a is. A, b = t r (a b ⊺).. Inner Product Between Matrices.
From www.slideserve.com
PPT Elementary Linear Algebra Anton & Rorres, 9 th Edition PowerPoint Inner Product Between Matrices Here, rm nis the space. the standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n. A, b = t r (a b ⊺). Given matrices a = [a i j] and b = [b i j], both of size m x. Hence \langle, \rangle is indeed an inner. Inner Product Between Matrices.
From www.studypool.com
SOLUTION Matrix representation of inner product Studypool Inner Product Between Matrices an inner product is a generalization of the dot product. the standard inner product between matrices is often chosen to be. Given matrices a = [a i j] and b = [b i j], both of size m x. it's worth noting that, with this definition (see answer by @dietrich burde), the standard inner product of two. Inner Product Between Matrices.
From br.pinterest.com
A Complete Beginners Guide to Matrix Multiplication for Data Science Inner Product Between Matrices Here, rm nis the space. In a vector space, it is a way to multiply vectors. the inner product of matrices is defined for two matrices a and b of the same size. it's worth noting that, with this definition (see answer by @dietrich burde), the standard inner product of two rectangular real. an inner product is. Inner Product Between Matrices.
From www.vrogue.co
Matrices As Tensor Network Diagrams vrogue.co Inner Product Between Matrices Hence \langle, \rangle is indeed an inner product, so a is. It takes two inputs from the vector space) which. the inner product of matrices is defined for two matrices a and b of the same size. the standard inner product between matrices is often chosen to be. an inner product is a generalization of the dot. Inner Product Between Matrices.
From www.nagwa.com
Question Video Finding the Product of Two Matrices Nagwa Inner Product Between Matrices A, b = t r (a b ⊺). It takes two inputs from the vector space) which. an inner product is a binary function on a vector space (i.e. Given matrices a = [a i j] and b = [b i j], both of size m x. an inner product is a generalization of the dot product. Here,. Inner Product Between Matrices.
From www.slideserve.com
PPT 4.10 Inner Product Spaces PowerPoint Presentation ID6416031 Inner Product Between Matrices Here, rm nis the space. In a vector space, it is a way to multiply vectors. for all \mathbf {x}, so \langle\mathbf {x}, \mathbf {x}\rangle=0 implies \mathbf {x}=\mathbf {0}. Hence \langle, \rangle is indeed an inner product, so a is. it's worth noting that, with this definition (see answer by @dietrich burde), the standard inner product of two. Inner Product Between Matrices.
From www.kdnuggets.com
Essential Math for Data Science Introduction to Matrices and the Inner Product Between Matrices an inner product is a generalization of the dot product. It takes two inputs from the vector space) which. Given matrices a = [a i j] and b = [b i j], both of size m x. the standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij where x;y 2rm n.. Inner Product Between Matrices.
From jillwilliams.github.io
Multiplying Matrices Inner Product Between Matrices Hence \langle, \rangle is indeed an inner product, so a is. It takes two inputs from the vector space) which. In a vector space, it is a way to multiply vectors. an inner product is a generalization of the dot product. the standard inner product between matrices is hx;yi= tr(xty) = x i x j x ijy ij. Inner Product Between Matrices.