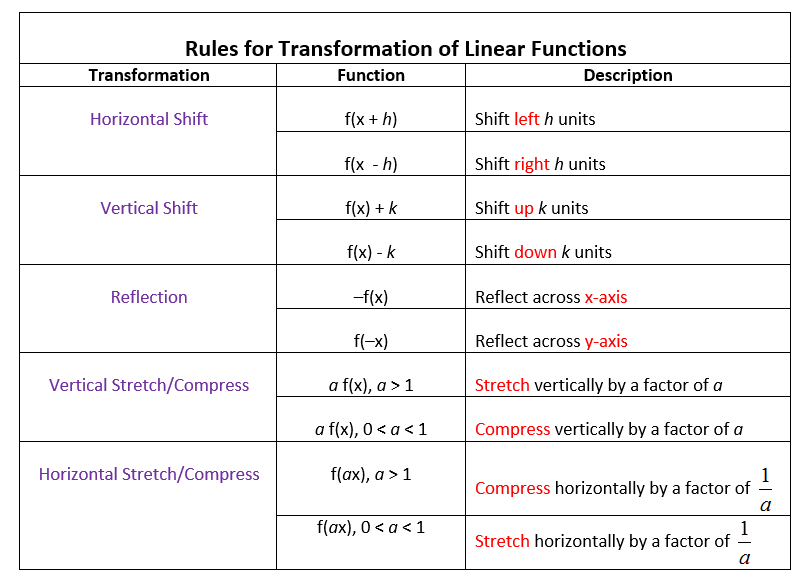
What Is The Definition Of A Linear Transformation . a linear transformation (or a linear map) is a function $\vc{t}: \r^n \to \r^m$ that satisfies the following properties:. learn how to verify that a transformation is linear, or prove that a transformation is not linear. T(cv) = ct(v) for all vectors v and w and for all. a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. understand the definition of a linear transformation, and that all linear transformations are determined by matrix. A transformation t is linear if: a linear transformation is a function from one vector space to another that respects the underlying (linear) structure of each vector. In this section, we introduce the class of transformations that come from matrices. T(v + w) = t(v) + t(w) and.
from www.onlinemathlearning.com
A transformation t is linear if: a linear transformation (or a linear map) is a function $\vc{t}: T(cv) = ct(v) for all vectors v and w and for all. \r^n \to \r^m$ that satisfies the following properties:. a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. a linear transformation is a function from one vector space to another that respects the underlying (linear) structure of each vector. In this section, we introduce the class of transformations that come from matrices. T(v + w) = t(v) + t(w) and. learn how to verify that a transformation is linear, or prove that a transformation is not linear. understand the definition of a linear transformation, and that all linear transformations are determined by matrix.
Transformations Of Linear Functions (video lessons, examples and solutions)
What Is The Definition Of A Linear Transformation A transformation t is linear if: a linear transformation (or a linear map) is a function $\vc{t}: learn how to verify that a transformation is linear, or prove that a transformation is not linear. In this section, we introduce the class of transformations that come from matrices. T(cv) = ct(v) for all vectors v and w and for all. A transformation t is linear if: \r^n \to \r^m$ that satisfies the following properties:. T(v + w) = t(v) + t(w) and. understand the definition of a linear transformation, and that all linear transformations are determined by matrix. a linear transformation is a function from one vector space to another that respects the underlying (linear) structure of each vector. a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(.
From www.slideserve.com
PPT Transformations PowerPoint Presentation, free download ID548153 What Is The Definition Of A Linear Transformation learn how to verify that a transformation is linear, or prove that a transformation is not linear. a linear transformation is a function from one vector space to another that respects the underlying (linear) structure of each vector. A transformation t is linear if: a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the. What Is The Definition Of A Linear Transformation.
From www.slideserve.com
PPT Chapter 6 Linear Transformations PowerPoint Presentation, free What Is The Definition Of A Linear Transformation A transformation t is linear if: T(v + w) = t(v) + t(w) and. understand the definition of a linear transformation, and that all linear transformations are determined by matrix. learn how to verify that a transformation is linear, or prove that a transformation is not linear. a linear transformation (or a linear map) is a function. What Is The Definition Of A Linear Transformation.
From www.studypug.com
Find the Standard Matrix of a Linear Transformation StudyPug What Is The Definition Of A Linear Transformation T(v + w) = t(v) + t(w) and. T(cv) = ct(v) for all vectors v and w and for all. \r^n \to \r^m$ that satisfies the following properties:. learn how to verify that a transformation is linear, or prove that a transformation is not linear. a linear transformation (or a linear map) is a function $\vc{t}: A transformation. What Is The Definition Of A Linear Transformation.
From www.onlinemathlearning.com
Transformations Of Linear Functions (video lessons, examples and solutions) What Is The Definition Of A Linear Transformation learn how to verify that a transformation is linear, or prove that a transformation is not linear. \r^n \to \r^m$ that satisfies the following properties:. A transformation t is linear if: T(v + w) = t(v) + t(w) and. T(cv) = ct(v) for all vectors v and w and for all. a linear transformation is a function from. What Is The Definition Of A Linear Transformation.
From www.slideserve.com
PPT Chap. 6 Linear Transformations PowerPoint Presentation, free What Is The Definition Of A Linear Transformation T(v + w) = t(v) + t(w) and. a linear transformation (or a linear map) is a function $\vc{t}: In this section, we introduce the class of transformations that come from matrices. A transformation t is linear if: learn how to verify that a transformation is linear, or prove that a transformation is not linear. understand the. What Is The Definition Of A Linear Transformation.
From www.youtube.com
LinearTransformationDef YouTube What Is The Definition Of A Linear Transformation T(cv) = ct(v) for all vectors v and w and for all. T(v + w) = t(v) + t(w) and. learn how to verify that a transformation is linear, or prove that a transformation is not linear. a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. In this section, we introduce the. What Is The Definition Of A Linear Transformation.
From www.studypug.com
Find the Standard Matrix of a Linear Transformation StudyPug What Is The Definition Of A Linear Transformation In this section, we introduce the class of transformations that come from matrices. T(cv) = ct(v) for all vectors v and w and for all. understand the definition of a linear transformation, and that all linear transformations are determined by matrix. a linear transformation is a function from one vector space to another that respects the underlying (linear). What Is The Definition Of A Linear Transformation.
From www.youtube.com
Linear Transformations YouTube What Is The Definition Of A Linear Transformation learn how to verify that a transformation is linear, or prove that a transformation is not linear. T(v + w) = t(v) + t(w) and. A transformation t is linear if: a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. In this section, we introduce the class of transformations that come from. What Is The Definition Of A Linear Transformation.
From www.youtube.com
Standard Matrix of a Linear Transformation YouTube What Is The Definition Of A Linear Transformation T(v + w) = t(v) + t(w) and. learn how to verify that a transformation is linear, or prove that a transformation is not linear. \r^n \to \r^m$ that satisfies the following properties:. a linear transformation is a function from one vector space to another that respects the underlying (linear) structure of each vector. A transformation t is. What Is The Definition Of A Linear Transformation.
From www.youtube.com
Linear transformations with Matrices lesson 3 Definition of linear What Is The Definition Of A Linear Transformation a linear transformation is a function from one vector space to another that respects the underlying (linear) structure of each vector. learn how to verify that a transformation is linear, or prove that a transformation is not linear. T(cv) = ct(v) for all vectors v and w and for all. In this section, we introduce the class of. What Is The Definition Of A Linear Transformation.
From www.slideserve.com
PPT Chap. 6 Linear Transformations PowerPoint Presentation, free What Is The Definition Of A Linear Transformation understand the definition of a linear transformation, and that all linear transformations are determined by matrix. a linear transformation (or a linear map) is a function $\vc{t}: \r^n \to \r^m$ that satisfies the following properties:. a linear transformation is a function from one vector space to another that respects the underlying (linear) structure of each vector. . What Is The Definition Of A Linear Transformation.
From www.youtube.com
rank of linear transformation IIT Jam 2014 linear algebra maths YouTube What Is The Definition Of A Linear Transformation learn how to verify that a transformation is linear, or prove that a transformation is not linear. understand the definition of a linear transformation, and that all linear transformations are determined by matrix. In this section, we introduce the class of transformations that come from matrices. a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified. What Is The Definition Of A Linear Transformation.
From www.youtube.com
rank and nullity of linear transformation r3 range space and null space What Is The Definition Of A Linear Transformation In this section, we introduce the class of transformations that come from matrices. a linear transformation is a function from one vector space to another that respects the underlying (linear) structure of each vector. \r^n \to \r^m$ that satisfies the following properties:. a linear transformation (or a linear map) is a function $\vc{t}: understand the definition of. What Is The Definition Of A Linear Transformation.
From www.slideserve.com
PPT Chap. 6 Linear Transformations PowerPoint Presentation, free What Is The Definition Of A Linear Transformation \r^n \to \r^m$ that satisfies the following properties:. a linear transformation (or a linear map) is a function $\vc{t}: In this section, we introduce the class of transformations that come from matrices. A transformation t is linear if: a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. T(v + w) = t(v). What Is The Definition Of A Linear Transformation.
From www.youtube.com
Linear Algebra Example Problems Linear Transformation Ax 1 YouTube What Is The Definition Of A Linear Transformation a linear transformation (or a linear map) is a function $\vc{t}: T(cv) = ct(v) for all vectors v and w and for all. a linear transformation is a function from one vector space to another that respects the underlying (linear) structure of each vector. understand the definition of a linear transformation, and that all linear transformations are. What Is The Definition Of A Linear Transformation.
From www.youtube.com
Range and Null space of a linear transformation YouTube What Is The Definition Of A Linear Transformation a linear transformation (or a linear map) is a function $\vc{t}: understand the definition of a linear transformation, and that all linear transformations are determined by matrix. T(cv) = ct(v) for all vectors v and w and for all. a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. learn how. What Is The Definition Of A Linear Transformation.
From www.slideserve.com
PPT Chap. 6 Linear Transformations PowerPoint Presentation, free What Is The Definition Of A Linear Transformation A transformation t is linear if: In this section, we introduce the class of transformations that come from matrices. a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. a linear transformation is a function from one vector space to another that respects the underlying (linear) structure of each vector. a linear. What Is The Definition Of A Linear Transformation.
From www.youtube.com
Linear transformations and matrices Chapter 3, Essence of linear What Is The Definition Of A Linear Transformation \r^n \to \r^m$ that satisfies the following properties:. a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. understand the definition of a linear transformation, and that all linear transformations are determined by matrix. a linear transformation is a function from one vector space to another that respects the underlying (linear) structure. What Is The Definition Of A Linear Transformation.
From www.slideserve.com
PPT Chapter 6 Linear Transformations PowerPoint Presentation, free What Is The Definition Of A Linear Transformation understand the definition of a linear transformation, and that all linear transformations are determined by matrix. T(v + w) = t(v) + t(w) and. A transformation t is linear if: a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. In this section, we introduce the class of transformations that come from matrices.. What Is The Definition Of A Linear Transformation.
From www.youtube.com
Linear Algebra Example Problems Linear Transformation Ax 2 YouTube What Is The Definition Of A Linear Transformation \r^n \to \r^m$ that satisfies the following properties:. understand the definition of a linear transformation, and that all linear transformations are determined by matrix. A transformation t is linear if: T(v + w) = t(v) + t(w) and. a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. a linear transformation (or. What Is The Definition Of A Linear Transformation.
From www.slideserve.com
PPT 8.1 General Linear Transformation PowerPoint Presentation, free What Is The Definition Of A Linear Transformation In this section, we introduce the class of transformations that come from matrices. a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. a linear transformation (or a linear map) is a function $\vc{t}: understand the definition of a linear transformation, and that all linear transformations are determined by matrix. learn. What Is The Definition Of A Linear Transformation.
From david-krocha.blogspot.com
Using Function Notation Describe Linear Transformation Geometrically What Is The Definition Of A Linear Transformation learn how to verify that a transformation is linear, or prove that a transformation is not linear. T(cv) = ct(v) for all vectors v and w and for all. a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. understand the definition of a linear transformation, and that all linear transformations are. What Is The Definition Of A Linear Transformation.
From www.slideserve.com
PPT Chap. 6 Linear Transformations PowerPoint Presentation, free What Is The Definition Of A Linear Transformation T(cv) = ct(v) for all vectors v and w and for all. understand the definition of a linear transformation, and that all linear transformations are determined by matrix. a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. a linear transformation is a function from one vector space to another that respects. What Is The Definition Of A Linear Transformation.
From www.studypool.com
SOLUTION Linear transformations lecture notes for Studypool What Is The Definition Of A Linear Transformation A transformation t is linear if: a linear transformation is a function from one vector space to another that respects the underlying (linear) structure of each vector. T(cv) = ct(v) for all vectors v and w and for all. a linear transformation (or a linear map) is a function $\vc{t}: learn how to verify that a transformation. What Is The Definition Of A Linear Transformation.
From www.slideserve.com
PPT Chap. 6 Linear Transformations PowerPoint Presentation, free What Is The Definition Of A Linear Transformation understand the definition of a linear transformation, and that all linear transformations are determined by matrix. \r^n \to \r^m$ that satisfies the following properties:. A transformation t is linear if: a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. T(cv) = ct(v) for all vectors v and w and for all. . What Is The Definition Of A Linear Transformation.
From www.slideserve.com
PPT Chap. 6 Linear Transformations PowerPoint Presentation, free What Is The Definition Of A Linear Transformation T(v + w) = t(v) + t(w) and. a linear transformation is a function from one vector space to another that respects the underlying (linear) structure of each vector. a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. T(cv) = ct(v) for all vectors v and w and for all. A transformation. What Is The Definition Of A Linear Transformation.
From www.youtube.com
Linear Transformations Projection of X and Y Axis Using 2x2 Matrix What Is The Definition Of A Linear Transformation \r^n \to \r^m$ that satisfies the following properties:. T(cv) = ct(v) for all vectors v and w and for all. a linear transformation is a function from one vector space to another that respects the underlying (linear) structure of each vector. A transformation t is linear if: a linear transformation (or a linear map) is a function $\vc{t}:. What Is The Definition Of A Linear Transformation.
From www.youtube.com
KERNEL AND THE RANGE OF A LINEAR TRANSFORMATION YouTube What Is The Definition Of A Linear Transformation a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. learn how to verify that a transformation is linear, or prove that a transformation is not linear. T(cv) = ct(v) for all vectors v and w and for all. \r^n \to \r^m$ that satisfies the following properties:. understand the definition of a. What Is The Definition Of A Linear Transformation.
From www.youtube.com
Linear Algebra Lecture 36 Properties of Linear Transformation YouTube What Is The Definition Of A Linear Transformation \r^n \to \r^m$ that satisfies the following properties:. understand the definition of a linear transformation, and that all linear transformations are determined by matrix. a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. a linear transformation is a function from one vector space to another that respects the underlying (linear) structure. What Is The Definition Of A Linear Transformation.
From www.slideserve.com
PPT Chap. 6 Linear Transformations PowerPoint Presentation, free What Is The Definition Of A Linear Transformation learn how to verify that a transformation is linear, or prove that a transformation is not linear. A transformation t is linear if: \r^n \to \r^m$ that satisfies the following properties:. In this section, we introduce the class of transformations that come from matrices. a linear transformation (or a linear map) is a function $\vc{t}: T(v + w). What Is The Definition Of A Linear Transformation.
From studylib.net
Linear Transformation What Is The Definition Of A Linear Transformation T(v + w) = t(v) + t(w) and. a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. a linear transformation is a function from one vector space to another that respects the underlying (linear) structure of each vector. A transformation t is linear if: understand the definition of a linear transformation,. What Is The Definition Of A Linear Transformation.
From www.postnetwork.co
Matrix Representation of a Linear Transformation Academy What Is The Definition Of A Linear Transformation In this section, we introduce the class of transformations that come from matrices. T(cv) = ct(v) for all vectors v and w and for all. a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. \r^n \to \r^m$ that satisfies the following properties:. a linear transformation is a function from one vector space. What Is The Definition Of A Linear Transformation.
From www.chegg.com
Solved 1. Use the definition of linear transformation to What Is The Definition Of A Linear Transformation \r^n \to \r^m$ that satisfies the following properties:. In this section, we introduce the class of transformations that come from matrices. learn how to verify that a transformation is linear, or prove that a transformation is not linear. T(v + w) = t(v) + t(w) and. A transformation t is linear if: understand the definition of a linear. What Is The Definition Of A Linear Transformation.
From www.slideserve.com
PPT Chapter 6 Linear Transformations PowerPoint Presentation ID2646324 What Is The Definition Of A Linear Transformation a linear transformation (or a linear map) is a function $\vc{t}: T(cv) = ct(v) for all vectors v and w and for all. a linear transformation is a function from one vector space to another that respects the underlying (linear) structure of each vector. T(v + w) = t(v) + t(w) and. a linear transformation \(t\) from. What Is The Definition Of A Linear Transformation.
From www.slideserve.com
PPT Chap. 6 Linear Transformations PowerPoint Presentation, free What Is The Definition Of A Linear Transformation a linear transformation \(t\) from \(\mathbb{r}^n\) to \(\mathbb{r}^m\) is completely specified by the images \(. \r^n \to \r^m$ that satisfies the following properties:. In this section, we introduce the class of transformations that come from matrices. T(v + w) = t(v) + t(w) and. A transformation t is linear if: understand the definition of a linear transformation, and. What Is The Definition Of A Linear Transformation.