What Is The Chromatic Number Of A Tree With N Vertices . Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree). What is it & why? Every finite tree with n vertices, with n > 1, has at least two terminal vertices (leaves). The smallest number of colors needed to color a graph g is called its chromatic number, and is often denoted χ(g). All trees with more than one vertex have the same chromatic number. Lecture 5 september 15, 2020 4 Sometimes γ( g ) is used,. The chromatic number of a graph g, denoted as χ (g), is the minimum number of colors required to color the vertices of a graph g in such a way that no. The chromatic number of a graph is the smallest number of colors needed to color the vertices of so that no two adjacent vertices share the same color (skiena 1990, p. What is the chromatic number of a tree on n 2 vertices? This minimal number of leaves is characteristic of path. (is this chromatic number by any chance. The degree of \(p_g\) is equal to the number of vertices of \(g\).
from www.chegg.com
This minimal number of leaves is characteristic of path. Every finite tree with n vertices, with n > 1, has at least two terminal vertices (leaves). Sometimes γ( g ) is used,. The chromatic number of a graph g, denoted as χ (g), is the minimum number of colors required to color the vertices of a graph g in such a way that no. What is it & why? The chromatic number of a graph is the smallest number of colors needed to color the vertices of so that no two adjacent vertices share the same color (skiena 1990, p. The smallest number of colors needed to color a graph g is called its chromatic number, and is often denoted χ(g). All trees with more than one vertex have the same chromatic number. (is this chromatic number by any chance. What is the chromatic number of a tree on n 2 vertices?
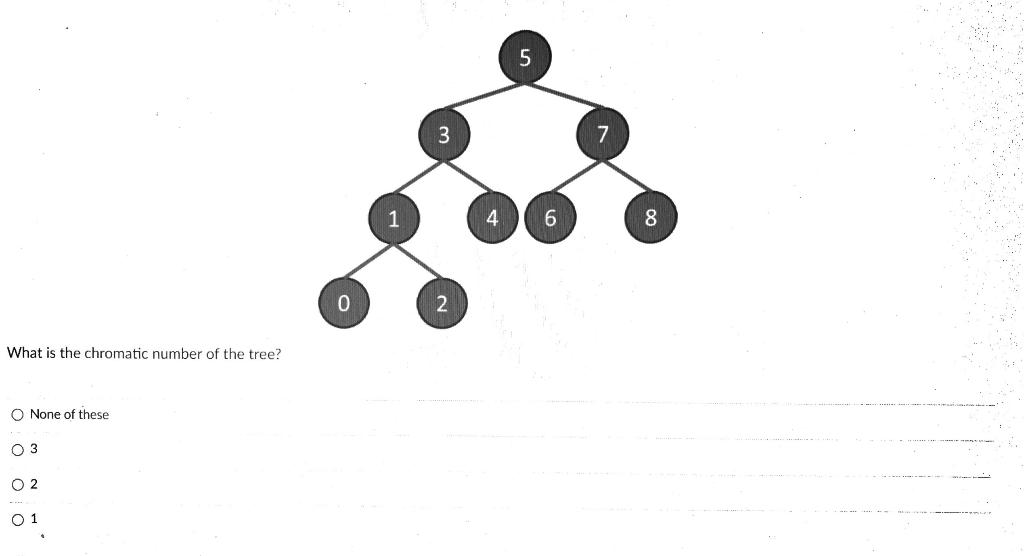
Solved 3 6 8 0 2 What is the chromatic number of the tree? O
What Is The Chromatic Number Of A Tree With N Vertices All trees with more than one vertex have the same chromatic number. All trees with more than one vertex have the same chromatic number. Sometimes γ( g ) is used,. (is this chromatic number by any chance. This minimal number of leaves is characteristic of path. The chromatic number of a graph is the smallest number of colors needed to color the vertices of so that no two adjacent vertices share the same color (skiena 1990, p. What is it & why? Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree). The smallest number of colors needed to color a graph g is called its chromatic number, and is often denoted χ(g). The degree of \(p_g\) is equal to the number of vertices of \(g\). What is the chromatic number of a tree on n 2 vertices? The chromatic number of a graph g, denoted as χ (g), is the minimum number of colors required to color the vertices of a graph g in such a way that no. Every finite tree with n vertices, with n > 1, has at least two terminal vertices (leaves). Lecture 5 september 15, 2020 4
From www.youtube.com
Proof Graph with n Vertices and n1 Edges is a Tree Graph Theory What Is The Chromatic Number Of A Tree With N Vertices What is it & why? Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree). Lecture 5 september 15, 2020 4 The smallest number of colors needed to color a graph g is called its chromatic number, and is often denoted χ(g). The degree of \(p_g\) is equal to the number of vertices of \(g\). Every finite. What Is The Chromatic Number Of A Tree With N Vertices.
From slideplayer.com
Discrete Mathematics Chapter8 Graphs. ppt download What Is The Chromatic Number Of A Tree With N Vertices Sometimes γ( g ) is used,. The chromatic number of a graph is the smallest number of colors needed to color the vertices of so that no two adjacent vertices share the same color (skiena 1990, p. The smallest number of colors needed to color a graph g is called its chromatic number, and is often denoted χ(g). Every finite. What Is The Chromatic Number Of A Tree With N Vertices.
From studylib.net
Chromatic Numbers_WS.. What Is The Chromatic Number Of A Tree With N Vertices Lecture 5 september 15, 2020 4 The degree of \(p_g\) is equal to the number of vertices of \(g\). The chromatic number of a graph g, denoted as χ (g), is the minimum number of colors required to color the vertices of a graph g in such a way that no. Sometimes γ( g ) is used,. (is this chromatic. What Is The Chromatic Number Of A Tree With N Vertices.
From www.researchgate.net
All trees with locatingchromatic number 3. Download Scientific Diagram What Is The Chromatic Number Of A Tree With N Vertices The degree of \(p_g\) is equal to the number of vertices of \(g\). Every finite tree with n vertices, with n > 1, has at least two terminal vertices (leaves). Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree). The chromatic number of a graph is the smallest number of colors needed to color the vertices. What Is The Chromatic Number Of A Tree With N Vertices.
From www.numerade.com
Prove that an nvertex graph is a tree if and only if its chromatic What Is The Chromatic Number Of A Tree With N Vertices The chromatic number of a graph is the smallest number of colors needed to color the vertices of so that no two adjacent vertices share the same color (skiena 1990, p. Lecture 5 september 15, 2020 4 Sometimes γ( g ) is used,. The degree of \(p_g\) is equal to the number of vertices of \(g\). The chromatic number of. What Is The Chromatic Number Of A Tree With N Vertices.
From www.researchgate.net
This figure shows how p(t) − q 2 evolves over time t with/without What Is The Chromatic Number Of A Tree With N Vertices This minimal number of leaves is characteristic of path. Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree). What is it & why? The smallest number of colors needed to color a graph g is called its chromatic number, and is often denoted χ(g). What is the chromatic number of a tree on n 2 vertices?. What Is The Chromatic Number Of A Tree With N Vertices.
From www.youtube.com
CHROMATIC NUMBERS GRAPH THEORY & TREES DISCRETE MATHEMATICS OU What Is The Chromatic Number Of A Tree With N Vertices Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree). Every finite tree with n vertices, with n > 1, has at least two terminal vertices (leaves). This minimal number of leaves is characteristic of path. The chromatic number of a graph g, denoted as χ (g), is the minimum number of colors required to color the. What Is The Chromatic Number Of A Tree With N Vertices.
From study.com
Chromatic Number of a Graph Definition & Example Lesson What Is The Chromatic Number Of A Tree With N Vertices All trees with more than one vertex have the same chromatic number. What is it & why? The smallest number of colors needed to color a graph g is called its chromatic number, and is often denoted χ(g). (is this chromatic number by any chance. Every finite tree with n vertices, with n > 1, has at least two terminal. What Is The Chromatic Number Of A Tree With N Vertices.
From www.researchgate.net
All trees of order í µí² > í µí¿ with locating chromatic number í What Is The Chromatic Number Of A Tree With N Vertices Every finite tree with n vertices, with n > 1, has at least two terminal vertices (leaves). Lecture 5 september 15, 2020 4 What is the chromatic number of a tree on n 2 vertices? Sometimes γ( g ) is used,. The degree of \(p_g\) is equal to the number of vertices of \(g\). (is this chromatic number by any. What Is The Chromatic Number Of A Tree With N Vertices.
From www.youtube.com
Chromatic polynomial of cycle on 4 vertices Part 2 YouTube What Is The Chromatic Number Of A Tree With N Vertices The smallest number of colors needed to color a graph g is called its chromatic number, and is often denoted χ(g). The degree of \(p_g\) is equal to the number of vertices of \(g\). Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree). The chromatic number of a graph g, denoted as χ (g), is the. What Is The Chromatic Number Of A Tree With N Vertices.
From jdh.hamkins.org
Math for sevenyearolds graph coloring, chromatic numbers, and What Is The Chromatic Number Of A Tree With N Vertices The chromatic number of a graph g, denoted as χ (g), is the minimum number of colors required to color the vertices of a graph g in such a way that no. This minimal number of leaves is characteristic of path. Sometimes γ( g ) is used,. Every finite tree with n vertices, with n > 1, has at least. What Is The Chromatic Number Of A Tree With N Vertices.
From www.gatevidyalay.com
Graph Coloring in Graph Theory Chromatic Number of Graphs Gate Vidyalay What Is The Chromatic Number Of A Tree With N Vertices All trees with more than one vertex have the same chromatic number. The degree of \(p_g\) is equal to the number of vertices of \(g\). What is the chromatic number of a tree on n 2 vertices? Lecture 5 september 15, 2020 4 What is it & why? (is this chromatic number by any chance. This minimal number of leaves. What Is The Chromatic Number Of A Tree With N Vertices.
From www.youtube.com
Chromatic Polynomial YouTube What Is The Chromatic Number Of A Tree With N Vertices All trees with more than one vertex have the same chromatic number. The chromatic number of a graph g, denoted as χ (g), is the minimum number of colors required to color the vertices of a graph g in such a way that no. The chromatic number of a graph is the smallest number of colors needed to color the. What Is The Chromatic Number Of A Tree With N Vertices.
From www.youtube.com
Chromatic number of a complete graph for "n" vertices is "n What Is The Chromatic Number Of A Tree With N Vertices (is this chromatic number by any chance. The chromatic number of a graph is the smallest number of colors needed to color the vertices of so that no two adjacent vertices share the same color (skiena 1990, p. This minimal number of leaves is characteristic of path. Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree).. What Is The Chromatic Number Of A Tree With N Vertices.
From www.chegg.com
Solved What is the chromatic number of the following graph? What Is The Chromatic Number Of A Tree With N Vertices (is this chromatic number by any chance. What is it & why? The degree of \(p_g\) is equal to the number of vertices of \(g\). This minimal number of leaves is characteristic of path. Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree). What is the chromatic number of a tree on n 2 vertices? Lecture. What Is The Chromatic Number Of A Tree With N Vertices.
From www.youtube.com
chromatic number of a treeGraph ColoringDiscrete Mathematics YouTube What Is The Chromatic Number Of A Tree With N Vertices Sometimes γ( g ) is used,. All trees with more than one vertex have the same chromatic number. Lecture 5 september 15, 2020 4 The chromatic number of a graph g, denoted as χ (g), is the minimum number of colors required to color the vertices of a graph g in such a way that no. This minimal number of. What Is The Chromatic Number Of A Tree With N Vertices.
From www.youtube.com
27. If G is a tree with n vertices then it has (n1) edges. GRAPH What Is The Chromatic Number Of A Tree With N Vertices The smallest number of colors needed to color a graph g is called its chromatic number, and is often denoted χ(g). The chromatic number of a graph g, denoted as χ (g), is the minimum number of colors required to color the vertices of a graph g in such a way that no. Lecture 5 september 15, 2020 4 Consider. What Is The Chromatic Number Of A Tree With N Vertices.
From www.gauthmath.com
Solved Question 2 (25 points) Tree Graphs What is the chromatic number What Is The Chromatic Number Of A Tree With N Vertices What is it & why? The chromatic number of a graph g, denoted as χ (g), is the minimum number of colors required to color the vertices of a graph g in such a way that no. This minimal number of leaves is characteristic of path. The degree of \(p_g\) is equal to the number of vertices of \(g\). The. What Is The Chromatic Number Of A Tree With N Vertices.
From www.youtube.com
15 Graph TheoryTheorems on TreesA tree with n vertices has n1 edges What Is The Chromatic Number Of A Tree With N Vertices Sometimes γ( g ) is used,. What is it & why? This minimal number of leaves is characteristic of path. The smallest number of colors needed to color a graph g is called its chromatic number, and is often denoted χ(g). Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree). The chromatic number of a graph. What Is The Chromatic Number Of A Tree With N Vertices.
From www.coursehero.com
[Solved] List 3 applications of graph coloring. Find the chromatic What Is The Chromatic Number Of A Tree With N Vertices Sometimes γ( g ) is used,. Lecture 5 september 15, 2020 4 This minimal number of leaves is characteristic of path. (is this chromatic number by any chance. Every finite tree with n vertices, with n > 1, has at least two terminal vertices (leaves). The chromatic number of a graph is the smallest number of colors needed to color. What Is The Chromatic Number Of A Tree With N Vertices.
From www.numerade.com
SOLVED5. Write the chromatic number of the following graphs [3 Marks What Is The Chromatic Number Of A Tree With N Vertices The chromatic number of a graph g, denoted as χ (g), is the minimum number of colors required to color the vertices of a graph g in such a way that no. This minimal number of leaves is characteristic of path. Lecture 5 september 15, 2020 4 Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree).. What Is The Chromatic Number Of A Tree With N Vertices.
From www.youtube.com
Prove that a tree with n vertices has n1 edges YouTube What Is The Chromatic Number Of A Tree With N Vertices Lecture 5 september 15, 2020 4 The smallest number of colors needed to color a graph g is called its chromatic number, and is often denoted χ(g). Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree). Every finite tree with n vertices, with n > 1, has at least two terminal vertices (leaves). The chromatic number. What Is The Chromatic Number Of A Tree With N Vertices.
From www.physicsforums.com
Number of edges in a tree digraph What Is The Chromatic Number Of A Tree With N Vertices Every finite tree with n vertices, with n > 1, has at least two terminal vertices (leaves). The smallest number of colors needed to color a graph g is called its chromatic number, and is often denoted χ(g). What is it & why? All trees with more than one vertex have the same chromatic number. This minimal number of leaves. What Is The Chromatic Number Of A Tree With N Vertices.
From www.chegg.com
Solved what is the chromatic number of the What Is The Chromatic Number Of A Tree With N Vertices The smallest number of colors needed to color a graph g is called its chromatic number, and is often denoted χ(g). Lecture 5 september 15, 2020 4 Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree). What is the chromatic number of a tree on n 2 vertices? This minimal number of leaves is characteristic of. What Is The Chromatic Number Of A Tree With N Vertices.
From www.slideserve.com
PPT Rooted Trees PowerPoint Presentation, free download ID549234 What Is The Chromatic Number Of A Tree With N Vertices What is the chromatic number of a tree on n 2 vertices? All trees with more than one vertex have the same chromatic number. The smallest number of colors needed to color a graph g is called its chromatic number, and is often denoted χ(g). (is this chromatic number by any chance. What is it & why? Every finite tree. What Is The Chromatic Number Of A Tree With N Vertices.
From www.slideshare.net
Graph theory What Is The Chromatic Number Of A Tree With N Vertices Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree). The degree of \(p_g\) is equal to the number of vertices of \(g\). This minimal number of leaves is characteristic of path. The smallest number of colors needed to color a graph g is called its chromatic number, and is often denoted χ(g). Lecture 5 september 15,. What Is The Chromatic Number Of A Tree With N Vertices.
From slidetodoc.com
Graph Colouring Tress in Graph Theory Chromatic numbers What Is The Chromatic Number Of A Tree With N Vertices Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree). The chromatic number of a graph g, denoted as χ (g), is the minimum number of colors required to color the vertices of a graph g in such a way that no. The chromatic number of a graph is the smallest number of colors needed to color. What Is The Chromatic Number Of A Tree With N Vertices.
From www.bartleby.com
Answered What is the chromatic number of (i)… bartleby What Is The Chromatic Number Of A Tree With N Vertices This minimal number of leaves is characteristic of path. Every finite tree with n vertices, with n > 1, has at least two terminal vertices (leaves). Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree). Lecture 5 september 15, 2020 4 (is this chromatic number by any chance. All trees with more than one vertex have. What Is The Chromatic Number Of A Tree With N Vertices.
From www.numerade.com
SOLVED1_ A labeled tree on n vertices is collection of line segments What Is The Chromatic Number Of A Tree With N Vertices Every finite tree with n vertices, with n > 1, has at least two terminal vertices (leaves). What is the chromatic number of a tree on n 2 vertices? The degree of \(p_g\) is equal to the number of vertices of \(g\). (is this chromatic number by any chance. Sometimes γ( g ) is used,. Consider an acyclic graph \(t_n\). What Is The Chromatic Number Of A Tree With N Vertices.
From www.chegg.com
Solved 3 6 8 0 2 What is the chromatic number of the tree? O What Is The Chromatic Number Of A Tree With N Vertices What is the chromatic number of a tree on n 2 vertices? All trees with more than one vertex have the same chromatic number. The smallest number of colors needed to color a graph g is called its chromatic number, and is often denoted χ(g). The chromatic number of a graph g, denoted as χ (g), is the minimum number. What Is The Chromatic Number Of A Tree With N Vertices.
From www.numerade.com
SOLVED What is the chromatic number of the above graph? List the What Is The Chromatic Number Of A Tree With N Vertices The degree of \(p_g\) is equal to the number of vertices of \(g\). (is this chromatic number by any chance. This minimal number of leaves is characteristic of path. Every finite tree with n vertices, with n > 1, has at least two terminal vertices (leaves). Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree). The. What Is The Chromatic Number Of A Tree With N Vertices.
From www.chegg.com
Solved 6. Prove the chromatic number of any tree is two. What Is The Chromatic Number Of A Tree With N Vertices The smallest number of colors needed to color a graph g is called its chromatic number, and is often denoted χ(g). Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree). Every finite tree with n vertices, with n > 1, has at least two terminal vertices (leaves). The degree of \(p_g\) is equal to the number. What Is The Chromatic Number Of A Tree With N Vertices.
From www.chegg.com
Solved (1 pt) What is the chromatic number of the above What Is The Chromatic Number Of A Tree With N Vertices What is it & why? Sometimes γ( g ) is used,. The degree of \(p_g\) is equal to the number of vertices of \(g\). The smallest number of colors needed to color a graph g is called its chromatic number, and is often denoted χ(g). This minimal number of leaves is characteristic of path. The chromatic number of a graph. What Is The Chromatic Number Of A Tree With N Vertices.
From kunduz.com
[ANSWERED] The chromatic number of the graph below is 3 The vertex on What Is The Chromatic Number Of A Tree With N Vertices Consider an acyclic graph \(t_n\) on \(n\) vertices (also known as a tree). The chromatic number of a graph g, denoted as χ (g), is the minimum number of colors required to color the vertices of a graph g in such a way that no. This minimal number of leaves is characteristic of path. What is the chromatic number of. What Is The Chromatic Number Of A Tree With N Vertices.
From www.researchgate.net
A proper vertex coloring of the Petersen graph with 3 colors, the What Is The Chromatic Number Of A Tree With N Vertices Lecture 5 september 15, 2020 4 (is this chromatic number by any chance. Sometimes γ( g ) is used,. The chromatic number of a graph g, denoted as χ (g), is the minimum number of colors required to color the vertices of a graph g in such a way that no. The smallest number of colors needed to color a. What Is The Chromatic Number Of A Tree With N Vertices.