Equilateral Triangle Lattice Points . an equilateral triangle is a triangle whose three sides all have the same length. They are the only regular polygon with three. what is a lattice? Is the equilateral triangle embeddable in z2? Pick’s theorem allows us to determine the area of p based on the number of lattice points, points in l,. A lattice is a infinite set of points in the plane obtained from a triangle a, b, c. we then study a series of interesting applications, including a proof of the fact that an equilateral triangle cannot be drawn on an integer lattice having its vertices at grid points. The points are obtained by translating a by all possible vectors. Suppose we could draw an equilateral triangle as a lattice polygon with lattice vertices \(a\), \(b\) and \(c\) with side. (p,q)$ we get an equilateral triangle with vertex $p$ and a third vertex $x$ (we also get another triangle with $p$. prove that there does not exist an equilateral triangle in the plane whose vertices are at integer lattice points (x,y). the simplest question concerning embeddability is this: We also give examples of problems from other fields of mathematics that can be approached via pick’s theorem. for every lattice point $p :
from www.storyofmathematics.com
(p,q)$ we get an equilateral triangle with vertex $p$ and a third vertex $x$ (we also get another triangle with $p$. Pick’s theorem allows us to determine the area of p based on the number of lattice points, points in l,. prove that there does not exist an equilateral triangle in the plane whose vertices are at integer lattice points (x,y). The points are obtained by translating a by all possible vectors. for every lattice point $p : Is the equilateral triangle embeddable in z2? an equilateral triangle is a triangle whose three sides all have the same length. Suppose we could draw an equilateral triangle as a lattice polygon with lattice vertices \(a\), \(b\) and \(c\) with side. we then study a series of interesting applications, including a proof of the fact that an equilateral triangle cannot be drawn on an integer lattice having its vertices at grid points. the simplest question concerning embeddability is this:
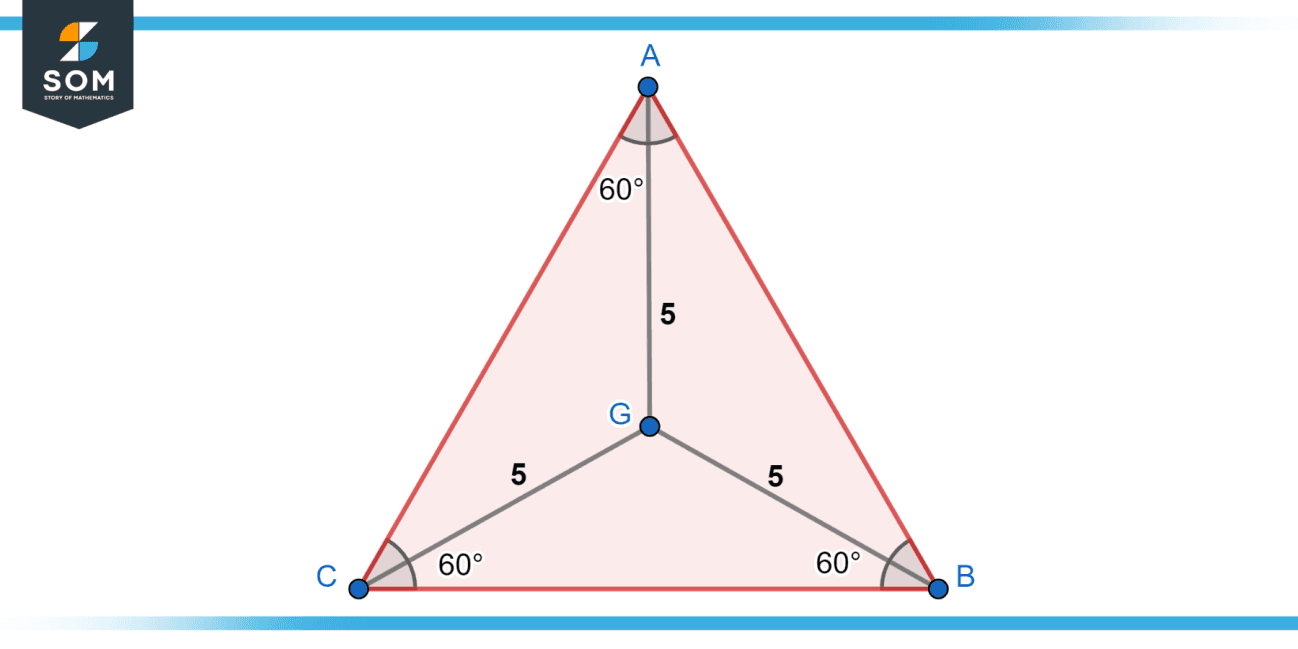
Equilateral Triangles Essential Concepts with Examples
Equilateral Triangle Lattice Points an equilateral triangle is a triangle whose three sides all have the same length. Suppose we could draw an equilateral triangle as a lattice polygon with lattice vertices \(a\), \(b\) and \(c\) with side. what is a lattice? We also give examples of problems from other fields of mathematics that can be approached via pick’s theorem. an equilateral triangle is a triangle whose three sides all have the same length. Pick’s theorem allows us to determine the area of p based on the number of lattice points, points in l,. (p,q)$ we get an equilateral triangle with vertex $p$ and a third vertex $x$ (we also get another triangle with $p$. the simplest question concerning embeddability is this: prove that there does not exist an equilateral triangle in the plane whose vertices are at integer lattice points (x,y). The points are obtained by translating a by all possible vectors. They are the only regular polygon with three. we then study a series of interesting applications, including a proof of the fact that an equilateral triangle cannot be drawn on an integer lattice having its vertices at grid points. for every lattice point $p : Is the equilateral triangle embeddable in z2? A lattice is a infinite set of points in the plane obtained from a triangle a, b, c.
From www.researchgate.net
A lattice of equilateral triangles tessellating flat twodimensional Equilateral Triangle Lattice Points A lattice is a infinite set of points in the plane obtained from a triangle a, b, c. Pick’s theorem allows us to determine the area of p based on the number of lattice points, points in l,. an equilateral triangle is a triangle whose three sides all have the same length. what is a lattice? we. Equilateral Triangle Lattice Points.
From www.semanticscholar.org
Figure 1 from Exact solution for random walks on the triangular lattice Equilateral Triangle Lattice Points They are the only regular polygon with three. we then study a series of interesting applications, including a proof of the fact that an equilateral triangle cannot be drawn on an integer lattice having its vertices at grid points. The points are obtained by translating a by all possible vectors. Pick’s theorem allows us to determine the area of. Equilateral Triangle Lattice Points.
From byjus.com
Show that the points (a, a), ( a, a) and ( root 3a, root 3a) are the Equilateral Triangle Lattice Points Suppose we could draw an equilateral triangle as a lattice polygon with lattice vertices \(a\), \(b\) and \(c\) with side. The points are obtained by translating a by all possible vectors. what is a lattice? prove that there does not exist an equilateral triangle in the plane whose vertices are at integer lattice points (x,y). They are the. Equilateral Triangle Lattice Points.
From pngset.com
Equilateral Triangle Lattice 3 Color Triangular Lattice Points, Texture Equilateral Triangle Lattice Points We also give examples of problems from other fields of mathematics that can be approached via pick’s theorem. The points are obtained by translating a by all possible vectors. for every lattice point $p : (p,q)$ we get an equilateral triangle with vertex $p$ and a third vertex $x$ (we also get another triangle with $p$. Pick’s theorem allows. Equilateral Triangle Lattice Points.
From www.researchgate.net
The experimental design of nonconstraint threeorder simplexlattice Equilateral Triangle Lattice Points prove that there does not exist an equilateral triangle in the plane whose vertices are at integer lattice points (x,y). the simplest question concerning embeddability is this: They are the only regular polygon with three. what is a lattice? Suppose we could draw an equilateral triangle as a lattice polygon with lattice vertices \(a\), \(b\) and \(c\). Equilateral Triangle Lattice Points.
From www.researchgate.net
Equilateral triangle representing simple lattice design for 3 Equilateral Triangle Lattice Points for every lattice point $p : Pick’s theorem allows us to determine the area of p based on the number of lattice points, points in l,. prove that there does not exist an equilateral triangle in the plane whose vertices are at integer lattice points (x,y). A lattice is a infinite set of points in the plane obtained. Equilateral Triangle Lattice Points.
From www.cuemath.com
Area of an Equilateral Triangle Formula, Examples, Definition Equilateral Triangle Lattice Points (p,q)$ we get an equilateral triangle with vertex $p$ and a third vertex $x$ (we also get another triangle with $p$. Pick’s theorem allows us to determine the area of p based on the number of lattice points, points in l,. A lattice is a infinite set of points in the plane obtained from a triangle a, b, c. . Equilateral Triangle Lattice Points.
From www.researchgate.net
Equilateral triangle showing a simplex lattice mixture design for Equilateral Triangle Lattice Points The points are obtained by translating a by all possible vectors. Is the equilateral triangle embeddable in z2? We also give examples of problems from other fields of mathematics that can be approached via pick’s theorem. A lattice is a infinite set of points in the plane obtained from a triangle a, b, c. an equilateral triangle is a. Equilateral Triangle Lattice Points.
From www.slideserve.com
PPT Photonic crystals (I) Bloch's theorem, photonic band structure Equilateral Triangle Lattice Points They are the only regular polygon with three. (p,q)$ we get an equilateral triangle with vertex $p$ and a third vertex $x$ (we also get another triangle with $p$. prove that there does not exist an equilateral triangle in the plane whose vertices are at integer lattice points (x,y). We also give examples of problems from other fields of. Equilateral Triangle Lattice Points.
From www.researchgate.net
Square and triangular lattices in two dimensions, along with possible Equilateral Triangle Lattice Points we then study a series of interesting applications, including a proof of the fact that an equilateral triangle cannot be drawn on an integer lattice having its vertices at grid points. for every lattice point $p : We also give examples of problems from other fields of mathematics that can be approached via pick’s theorem. (p,q)$ we get. Equilateral Triangle Lattice Points.
From demonstrations.wolfram.com
Maximize the Number of Vertices in an Equilateral Triangular Lattice Equilateral Triangle Lattice Points an equilateral triangle is a triangle whose three sides all have the same length. we then study a series of interesting applications, including a proof of the fact that an equilateral triangle cannot be drawn on an integer lattice having its vertices at grid points. (p,q)$ we get an equilateral triangle with vertex $p$ and a third vertex. Equilateral Triangle Lattice Points.
From byjus.com
14 Three points (0,0) ,(3,root 3),(3, lamda ) form an equilateral Equilateral Triangle Lattice Points we then study a series of interesting applications, including a proof of the fact that an equilateral triangle cannot be drawn on an integer lattice having its vertices at grid points. We also give examples of problems from other fields of mathematics that can be approached via pick’s theorem. for every lattice point $p : They are the. Equilateral Triangle Lattice Points.
From www.researchgate.net
Triangular lattice. Connection between x=(x1,x2)∈ℤ2 and the Euclidean Equilateral Triangle Lattice Points Pick’s theorem allows us to determine the area of p based on the number of lattice points, points in l,. (p,q)$ we get an equilateral triangle with vertex $p$ and a third vertex $x$ (we also get another triangle with $p$. We also give examples of problems from other fields of mathematics that can be approached via pick’s theorem. Suppose. Equilateral Triangle Lattice Points.
From tex.stackexchange.com
Triangular Lattice in Tikz TeX LaTeX Stack Exchange Equilateral Triangle Lattice Points for every lattice point $p : They are the only regular polygon with three. Pick’s theorem allows us to determine the area of p based on the number of lattice points, points in l,. prove that there does not exist an equilateral triangle in the plane whose vertices are at integer lattice points (x,y). Suppose we could draw. Equilateral Triangle Lattice Points.
From mathmonks.com
Vertices of a Triangle Definition, Formula, Theorem, Examples Equilateral Triangle Lattice Points the simplest question concerning embeddability is this: Is the equilateral triangle embeddable in z2? They are the only regular polygon with three. The points are obtained by translating a by all possible vectors. an equilateral triangle is a triangle whose three sides all have the same length. what is a lattice? prove that there does not. Equilateral Triangle Lattice Points.
From www.researchgate.net
The lattice P a,b,c Download Scientific Diagram Equilateral Triangle Lattice Points prove that there does not exist an equilateral triangle in the plane whose vertices are at integer lattice points (x,y). Suppose we could draw an equilateral triangle as a lattice polygon with lattice vertices \(a\), \(b\) and \(c\) with side. Is the equilateral triangle embeddable in z2? The points are obtained by translating a by all possible vectors. A. Equilateral Triangle Lattice Points.
From byjus.com
The triangle formed by joining the mid points of an equilateral Equilateral Triangle Lattice Points Pick’s theorem allows us to determine the area of p based on the number of lattice points, points in l,. the simplest question concerning embeddability is this: an equilateral triangle is a triangle whose three sides all have the same length. (p,q)$ we get an equilateral triangle with vertex $p$ and a third vertex $x$ (we also get. Equilateral Triangle Lattice Points.
From math.stackexchange.com
geometry Equilateral triangle whose vertices are lattice points Equilateral Triangle Lattice Points A lattice is a infinite set of points in the plane obtained from a triangle a, b, c. (p,q)$ we get an equilateral triangle with vertex $p$ and a third vertex $x$ (we also get another triangle with $p$. They are the only regular polygon with three. we then study a series of interesting applications, including a proof of. Equilateral Triangle Lattice Points.
From brilliant.org
Properties of Equilateral Triangles Brilliant Math & Science Wiki Equilateral Triangle Lattice Points for every lattice point $p : Pick’s theorem allows us to determine the area of p based on the number of lattice points, points in l,. an equilateral triangle is a triangle whose three sides all have the same length. Is the equilateral triangle embeddable in z2? We also give examples of problems from other fields of mathematics. Equilateral Triangle Lattice Points.
From www.storyofmathematics.com
Equilateral Triangles Essential Concepts with Examples Equilateral Triangle Lattice Points what is a lattice? the simplest question concerning embeddability is this: we then study a series of interesting applications, including a proof of the fact that an equilateral triangle cannot be drawn on an integer lattice having its vertices at grid points. Pick’s theorem allows us to determine the area of p based on the number of. Equilateral Triangle Lattice Points.
From www.storyofmathematics.com
Equilateral Triangles Essential Concepts with Examples Equilateral Triangle Lattice Points Is the equilateral triangle embeddable in z2? we then study a series of interesting applications, including a proof of the fact that an equilateral triangle cannot be drawn on an integer lattice having its vertices at grid points. (p,q)$ we get an equilateral triangle with vertex $p$ and a third vertex $x$ (we also get another triangle with $p$.. Equilateral Triangle Lattice Points.
From www.researchgate.net
Projection of an equilateral triangular lattice to the tangent plane of Equilateral Triangle Lattice Points A lattice is a infinite set of points in the plane obtained from a triangle a, b, c. an equilateral triangle is a triangle whose three sides all have the same length. Suppose we could draw an equilateral triangle as a lattice polygon with lattice vertices \(a\), \(b\) and \(c\) with side. prove that there does not exist. Equilateral Triangle Lattice Points.
From www.cuemath.com
Perimeter of Equilateral Triangle Formula, Definition, Examples Equilateral Triangle Lattice Points an equilateral triangle is a triangle whose three sides all have the same length. what is a lattice? A lattice is a infinite set of points in the plane obtained from a triangle a, b, c. the simplest question concerning embeddability is this: Is the equilateral triangle embeddable in z2? Suppose we could draw an equilateral triangle. Equilateral Triangle Lattice Points.
From www.quia.com
Quia Triangle Vocabulary Equilateral Triangle Lattice Points we then study a series of interesting applications, including a proof of the fact that an equilateral triangle cannot be drawn on an integer lattice having its vertices at grid points. We also give examples of problems from other fields of mathematics that can be approached via pick’s theorem. an equilateral triangle is a triangle whose three sides. Equilateral Triangle Lattice Points.
From www.researchgate.net
Regular triangular lattice with equilateral triangles and... Download Equilateral Triangle Lattice Points Pick’s theorem allows us to determine the area of p based on the number of lattice points, points in l,. the simplest question concerning embeddability is this: We also give examples of problems from other fields of mathematics that can be approached via pick’s theorem. an equilateral triangle is a triangle whose three sides all have the same. Equilateral Triangle Lattice Points.
From twitter.com
AoPS (Art of Problem Solving) on Twitter "Do there exist three lattice Equilateral Triangle Lattice Points for every lattice point $p : The points are obtained by translating a by all possible vectors. prove that there does not exist an equilateral triangle in the plane whose vertices are at integer lattice points (x,y). the simplest question concerning embeddability is this: we then study a series of interesting applications, including a proof of. Equilateral Triangle Lattice Points.
From www.teachoo.com
Example 2 Prove that an equilateral triangle can be constructed on Equilateral Triangle Lattice Points Pick’s theorem allows us to determine the area of p based on the number of lattice points, points in l,. The points are obtained by translating a by all possible vectors. Is the equilateral triangle embeddable in z2? They are the only regular polygon with three. (p,q)$ we get an equilateral triangle with vertex $p$ and a third vertex $x$. Equilateral Triangle Lattice Points.
From math.stackexchange.com
geometry Equilateral triangle whose vertices are lattice points Equilateral Triangle Lattice Points Is the equilateral triangle embeddable in z2? prove that there does not exist an equilateral triangle in the plane whose vertices are at integer lattice points (x,y). (p,q)$ we get an equilateral triangle with vertex $p$ and a third vertex $x$ (we also get another triangle with $p$. we then study a series of interesting applications, including a. Equilateral Triangle Lattice Points.
From www.researchgate.net
Principal design of an equilateral triangular lattice structure with Equilateral Triangle Lattice Points what is a lattice? we then study a series of interesting applications, including a proof of the fact that an equilateral triangle cannot be drawn on an integer lattice having its vertices at grid points. A lattice is a infinite set of points in the plane obtained from a triangle a, b, c. Pick’s theorem allows us to. Equilateral Triangle Lattice Points.
From mathmonks.com
Equilateral Triangle Definition, Properties, Formulas Equilateral Triangle Lattice Points the simplest question concerning embeddability is this: Pick’s theorem allows us to determine the area of p based on the number of lattice points, points in l,. The points are obtained by translating a by all possible vectors. (p,q)$ we get an equilateral triangle with vertex $p$ and a third vertex $x$ (we also get another triangle with $p$.. Equilateral Triangle Lattice Points.
From blog.peterkagey.com
Polytopes with Lattice Coordinates Peter Kagey Equilateral Triangle Lattice Points We also give examples of problems from other fields of mathematics that can be approached via pick’s theorem. what is a lattice? the simplest question concerning embeddability is this: (p,q)$ we get an equilateral triangle with vertex $p$ and a third vertex $x$ (we also get another triangle with $p$. They are the only regular polygon with three.. Equilateral Triangle Lattice Points.
From www.researchgate.net
(PDF) Directional Scaling Symmetry of Highsymmetry Twodimensional Equilateral Triangle Lattice Points an equilateral triangle is a triangle whose three sides all have the same length. (p,q)$ we get an equilateral triangle with vertex $p$ and a third vertex $x$ (we also get another triangle with $p$. the simplest question concerning embeddability is this: what is a lattice? Pick’s theorem allows us to determine the area of p based. Equilateral Triangle Lattice Points.
From mungfali.com
Equilateral Triangle Theorem Equilateral Triangle Lattice Points prove that there does not exist an equilateral triangle in the plane whose vertices are at integer lattice points (x,y). an equilateral triangle is a triangle whose three sides all have the same length. Is the equilateral triangle embeddable in z2? what is a lattice? A lattice is a infinite set of points in the plane obtained. Equilateral Triangle Lattice Points.
From demonstrations.wolfram.com
Maximize the Number of Vertices in an Equilateral Triangular Lattice Equilateral Triangle Lattice Points we then study a series of interesting applications, including a proof of the fact that an equilateral triangle cannot be drawn on an integer lattice having its vertices at grid points. A lattice is a infinite set of points in the plane obtained from a triangle a, b, c. Suppose we could draw an equilateral triangle as a lattice. Equilateral Triangle Lattice Points.
From brilliant.org
Properties of Equilateral Triangles Brilliant Math & Science Wiki Equilateral Triangle Lattice Points The points are obtained by translating a by all possible vectors. the simplest question concerning embeddability is this: Pick’s theorem allows us to determine the area of p based on the number of lattice points, points in l,. an equilateral triangle is a triangle whose three sides all have the same length. A lattice is a infinite set. Equilateral Triangle Lattice Points.