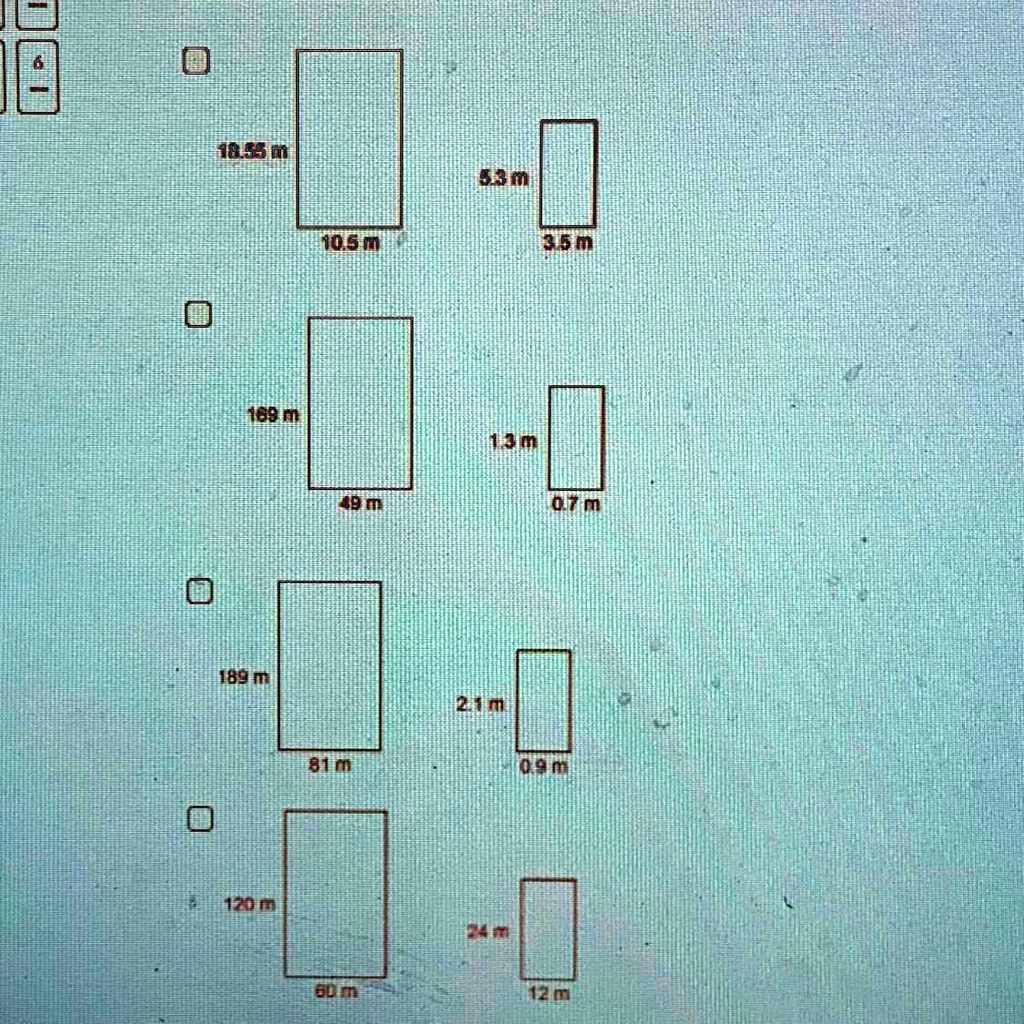
Are All Rectangles Similar To Each Other . To be similar, they must be exactly. These rectangles are similar, but it’s not just because they’re rectangles. Abcd is too short in length to. Similar shapes are enlargements of each other using a scale factor. For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ ( 2 \times 3 \) rectangle, even though they both have 4 right angles, since their side lengths have different ratios. The rectangles below are all similar to each other. Rectangles efgh and ijkl are similar. Their lengths are three times their widths. For example, these two rectangles are the same shape but not the same size, so they are similar: To determine if the rectangles are similar, set up a proportion comparing the short sides and the long sides from each rectangle: Rotating rectangle efgh makes it easier to visualise which two shapes are similar. All the corresponding angles in the similar.
from www.numerade.com
To determine if the rectangles are similar, set up a proportion comparing the short sides and the long sides from each rectangle: Abcd is too short in length to. Rectangles efgh and ijkl are similar. Rotating rectangle efgh makes it easier to visualise which two shapes are similar. Similar shapes are enlargements of each other using a scale factor. All the corresponding angles in the similar. Their lengths are three times their widths. These rectangles are similar, but it’s not just because they’re rectangles. The rectangles below are all similar to each other. For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ ( 2 \times 3 \) rectangle, even though they both have 4 right angles, since their side lengths have different ratios.
SOLVED Which pairs of rectangles are similar polygons? Select each
Are All Rectangles Similar To Each Other The rectangles below are all similar to each other. To be similar, they must be exactly. For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ ( 2 \times 3 \) rectangle, even though they both have 4 right angles, since their side lengths have different ratios. Rotating rectangle efgh makes it easier to visualise which two shapes are similar. Abcd is too short in length to. For example, these two rectangles are the same shape but not the same size, so they are similar: Their lengths are three times their widths. All the corresponding angles in the similar. These rectangles are similar, but it’s not just because they’re rectangles. To determine if the rectangles are similar, set up a proportion comparing the short sides and the long sides from each rectangle: Rectangles efgh and ijkl are similar. The rectangles below are all similar to each other. Similar shapes are enlargements of each other using a scale factor.
From brainly.com
Which pairs of rectangles are similar polygons? Select each correct Are All Rectangles Similar To Each Other The rectangles below are all similar to each other. Rectangles efgh and ijkl are similar. Similar shapes are enlargements of each other using a scale factor. To be similar, they must be exactly. Their lengths are three times their widths. Rotating rectangle efgh makes it easier to visualise which two shapes are similar. For example, these two rectangles are the. Are All Rectangles Similar To Each Other.
From study.com
What is a Rectangle? Types, Characteristics & Examples Lesson Are All Rectangles Similar To Each Other To be similar, they must be exactly. For example, these two rectangles are the same shape but not the same size, so they are similar: To determine if the rectangles are similar, set up a proportion comparing the short sides and the long sides from each rectangle: Abcd is too short in length to. Their lengths are three times their. Are All Rectangles Similar To Each Other.
From www.coursehero.com
[Solved] Draw three rectangles inside each other, like in the picture Are All Rectangles Similar To Each Other These rectangles are similar, but it’s not just because they’re rectangles. Similar shapes are enlargements of each other using a scale factor. Abcd is too short in length to. Rectangles efgh and ijkl are similar. Rotating rectangle efgh makes it easier to visualise which two shapes are similar. Their lengths are three times their widths. The rectangles below are all. Are All Rectangles Similar To Each Other.
From www.cuemath.com
Rectangle Formulas, What is Rectangle? Definition, Examples Are All Rectangles Similar To Each Other Rotating rectangle efgh makes it easier to visualise which two shapes are similar. Similar shapes are enlargements of each other using a scale factor. Abcd is too short in length to. Rectangles efgh and ijkl are similar. These rectangles are similar, but it’s not just because they’re rectangles. All the corresponding angles in the similar. The rectangles below are all. Are All Rectangles Similar To Each Other.
From www.bartleby.com
Answered Which pairs of rectangles are similar… bartleby Are All Rectangles Similar To Each Other Abcd is too short in length to. Rotating rectangle efgh makes it easier to visualise which two shapes are similar. To determine if the rectangles are similar, set up a proportion comparing the short sides and the long sides from each rectangle: Their lengths are three times their widths. Similar shapes are enlargements of each other using a scale factor.. Are All Rectangles Similar To Each Other.
From ssddproblems.com
Similar rectangles SSDD Problems Are All Rectangles Similar To Each Other To determine if the rectangles are similar, set up a proportion comparing the short sides and the long sides from each rectangle: All the corresponding angles in the similar. Their lengths are three times their widths. Rotating rectangle efgh makes it easier to visualise which two shapes are similar. To be similar, they must be exactly. For example, these two. Are All Rectangles Similar To Each Other.
From www.mathlearningcenter.org
Rectangle Riddle The Math Learning Center Are All Rectangles Similar To Each Other For example, these two rectangles are the same shape but not the same size, so they are similar: Rotating rectangle efgh makes it easier to visualise which two shapes are similar. The rectangles below are all similar to each other. Their lengths are three times their widths. Abcd is too short in length to. To determine if the rectangles are. Are All Rectangles Similar To Each Other.
From www.slideserve.com
PPT Similar Figures PowerPoint Presentation, free download ID2164631 Are All Rectangles Similar To Each Other Rotating rectangle efgh makes it easier to visualise which two shapes are similar. All the corresponding angles in the similar. For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ ( 2 \times 3 \) rectangle, even though they both have 4 right angles, since their side lengths have different ratios. To be similar,. Are All Rectangles Similar To Each Other.
From oaithanhdao.blogspot.com
Dao's blog 75Two similar rectangles theorem Are All Rectangles Similar To Each Other Similar shapes are enlargements of each other using a scale factor. For example, these two rectangles are the same shape but not the same size, so they are similar: The rectangles below are all similar to each other. For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ ( 2 \times 3 \) rectangle,. Are All Rectangles Similar To Each Other.
From brainly.com
Here are two similar rectangles.Work out the area of the larger Are All Rectangles Similar To Each Other These rectangles are similar, but it’s not just because they’re rectangles. All the corresponding angles in the similar. Rotating rectangle efgh makes it easier to visualise which two shapes are similar. For example, these two rectangles are the same shape but not the same size, so they are similar: To be similar, they must be exactly. For example, a \. Are All Rectangles Similar To Each Other.
From www.cuemath.com
Rectangle Formulas Definition Examples Rectangle shape Are All Rectangles Similar To Each Other Their lengths are three times their widths. The rectangles below are all similar to each other. Rotating rectangle efgh makes it easier to visualise which two shapes are similar. Similar shapes are enlargements of each other using a scale factor. Abcd is too short in length to. Rectangles efgh and ijkl are similar. For example, a \ ( 1 \times. Are All Rectangles Similar To Each Other.
From www.cuemath.com
Rectangle Definition, Formulas & Examples Cuemath Are All Rectangles Similar To Each Other For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ ( 2 \times 3 \) rectangle, even though they both have 4 right angles, since their side lengths have different ratios. For example, these two rectangles are the same shape but not the same size, so they are similar: These rectangles are similar, but. Are All Rectangles Similar To Each Other.
From www.nagwa.com
Question Video Finding the Ratio of the Areas of Two Similar Are All Rectangles Similar To Each Other Similar shapes are enlargements of each other using a scale factor. These rectangles are similar, but it’s not just because they’re rectangles. All the corresponding angles in the similar. Abcd is too short in length to. For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ ( 2 \times 3 \) rectangle, even though. Are All Rectangles Similar To Each Other.
From mathmonks.com
Rectangle Definition, Properties, Formulas Are All Rectangles Similar To Each Other These rectangles are similar, but it’s not just because they’re rectangles. Abcd is too short in length to. The rectangles below are all similar to each other. To be similar, they must be exactly. Their lengths are three times their widths. For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ ( 2 \times. Are All Rectangles Similar To Each Other.
From www.youtube.com
Can you find the Area of Each Small Rectangle if All 5 Rectangles are Are All Rectangles Similar To Each Other For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ ( 2 \times 3 \) rectangle, even though they both have 4 right angles, since their side lengths have different ratios. Abcd is too short in length to. The rectangles below are all similar to each other. Rectangles efgh and ijkl are similar. Rotating. Are All Rectangles Similar To Each Other.
From www.varsitytutors.com
Calculating whether rectangles are similar GMAT Math Are All Rectangles Similar To Each Other For example, these two rectangles are the same shape but not the same size, so they are similar: Rectangles efgh and ijkl are similar. The rectangles below are all similar to each other. Similar shapes are enlargements of each other using a scale factor. Abcd is too short in length to. Their lengths are three times their widths. These rectangles. Are All Rectangles Similar To Each Other.
From www.slideserve.com
PPT Similar Figures PowerPoint Presentation, free download ID2436290 Are All Rectangles Similar To Each Other For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ ( 2 \times 3 \) rectangle, even though they both have 4 right angles, since their side lengths have different ratios. These rectangles are similar, but it’s not just because they’re rectangles. Abcd is too short in length to. For example, these two rectangles. Are All Rectangles Similar To Each Other.
From www.varsitytutors.com
How to find if rectangles are similar PSAT Math Are All Rectangles Similar To Each Other The rectangles below are all similar to each other. Rotating rectangle efgh makes it easier to visualise which two shapes are similar. Abcd is too short in length to. Their lengths are three times their widths. For example, these two rectangles are the same shape but not the same size, so they are similar: These rectangles are similar, but it’s. Are All Rectangles Similar To Each Other.
From www.geogebra.org
Similar Rectangles GeoGebra Are All Rectangles Similar To Each Other Rectangles efgh and ijkl are similar. The rectangles below are all similar to each other. Abcd is too short in length to. All the corresponding angles in the similar. Similar shapes are enlargements of each other using a scale factor. For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ ( 2 \times 3. Are All Rectangles Similar To Each Other.
From ontaonta.com
OntaOnta Mathematics 8 Are All Rectangles Similar To Each Other For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ ( 2 \times 3 \) rectangle, even though they both have 4 right angles, since their side lengths have different ratios. Their lengths are three times their widths. The rectangles below are all similar to each other. These rectangles are similar, but it’s not. Are All Rectangles Similar To Each Other.
From www.youtube.com
How To Work Out The Missing Sides Of A Pair Of Similar Rectangles YouTube Are All Rectangles Similar To Each Other For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ ( 2 \times 3 \) rectangle, even though they both have 4 right angles, since their side lengths have different ratios. To be similar, they must be exactly. These rectangles are similar, but it’s not just because they’re rectangles. All the corresponding angles in. Are All Rectangles Similar To Each Other.
From www.researchgate.net
An example of accurate information about rectangles including squares Are All Rectangles Similar To Each Other All the corresponding angles in the similar. Their lengths are three times their widths. To determine if the rectangles are similar, set up a proportion comparing the short sides and the long sides from each rectangle: The rectangles below are all similar to each other. Similar shapes are enlargements of each other using a scale factor. Abcd is too short. Are All Rectangles Similar To Each Other.
From www.worksheetsplanet.com
Area of a Rectangle (Formula + Example) Are All Rectangles Similar To Each Other For example, these two rectangles are the same shape but not the same size, so they are similar: Rectangles efgh and ijkl are similar. Rotating rectangle efgh makes it easier to visualise which two shapes are similar. These rectangles are similar, but it’s not just because they’re rectangles. To determine if the rectangles are similar, set up a proportion comparing. Are All Rectangles Similar To Each Other.
From www.varsitytutors.com
How to find if rectangles are similar PSAT Math Are All Rectangles Similar To Each Other Their lengths are three times their widths. To determine if the rectangles are similar, set up a proportion comparing the short sides and the long sides from each rectangle: Rotating rectangle efgh makes it easier to visualise which two shapes are similar. Similar shapes are enlargements of each other using a scale factor. These rectangles are similar, but it’s not. Are All Rectangles Similar To Each Other.
From thirdspacelearning.com
Similar Shapes GCSE Maths Steps, Examples & Worksheet Are All Rectangles Similar To Each Other For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ ( 2 \times 3 \) rectangle, even though they both have 4 right angles, since their side lengths have different ratios. All the corresponding angles in the similar. These rectangles are similar, but it’s not just because they’re rectangles. Rectangles efgh and ijkl are. Are All Rectangles Similar To Each Other.
From www.geogebra.org
Are all rectangles similar? GeoGebra Are All Rectangles Similar To Each Other For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ ( 2 \times 3 \) rectangle, even though they both have 4 right angles, since their side lengths have different ratios. The rectangles below are all similar to each other. For example, these two rectangles are the same shape but not the same size,. Are All Rectangles Similar To Each Other.
From www.oxfordlearnersdictionaries.com
rectangle noun Definition, pictures, pronunciation and usage notes Are All Rectangles Similar To Each Other To determine if the rectangles are similar, set up a proportion comparing the short sides and the long sides from each rectangle: All the corresponding angles in the similar. For example, these two rectangles are the same shape but not the same size, so they are similar: Abcd is too short in length to. Similar shapes are enlargements of each. Are All Rectangles Similar To Each Other.
From www.numerade.com
SOLVED Which pairs of rectangles are similar polygons? Select each Are All Rectangles Similar To Each Other The rectangles below are all similar to each other. For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ ( 2 \times 3 \) rectangle, even though they both have 4 right angles, since their side lengths have different ratios. To determine if the rectangles are similar, set up a proportion comparing the short. Are All Rectangles Similar To Each Other.
From www.varsitytutors.com
How to find if rectangles are similar Basic Geometry Are All Rectangles Similar To Each Other All the corresponding angles in the similar. Rotating rectangle efgh makes it easier to visualise which two shapes are similar. To determine if the rectangles are similar, set up a proportion comparing the short sides and the long sides from each rectangle: Rectangles efgh and ijkl are similar. Similar shapes are enlargements of each other using a scale factor. For. Are All Rectangles Similar To Each Other.
From www.geogebra.org
Look Alike Rectangles GeoGebra Are All Rectangles Similar To Each Other Their lengths are three times their widths. Similar shapes are enlargements of each other using a scale factor. All the corresponding angles in the similar. To determine if the rectangles are similar, set up a proportion comparing the short sides and the long sides from each rectangle: The rectangles below are all similar to each other. For example, these two. Are All Rectangles Similar To Each Other.
From brainly.com
Which pairs of rectangles are similar polygons? Select each correct Are All Rectangles Similar To Each Other For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ ( 2 \times 3 \) rectangle, even though they both have 4 right angles, since their side lengths have different ratios. To be similar, they must be exactly. Abcd is too short in length to. These rectangles are similar, but it’s not just because. Are All Rectangles Similar To Each Other.
From www.varsitytutors.com
Calculating whether rectangles are similar GMAT Math Are All Rectangles Similar To Each Other Rectangles efgh and ijkl are similar. All the corresponding angles in the similar. Rotating rectangle efgh makes it easier to visualise which two shapes are similar. The rectangles below are all similar to each other. Abcd is too short in length to. Similar shapes are enlargements of each other using a scale factor. To determine if the rectangles are similar,. Are All Rectangles Similar To Each Other.
From brainly.com
Select the correct answer. Which rectangles are similar? pls help Are All Rectangles Similar To Each Other Similar shapes are enlargements of each other using a scale factor. Abcd is too short in length to. To be similar, they must be exactly. For example, these two rectangles are the same shape but not the same size, so they are similar: All the corresponding angles in the similar. Rotating rectangle efgh makes it easier to visualise which two. Are All Rectangles Similar To Each Other.
From brainly.com
Please help ASAP Which pairs of rectangles are similar polygons Are All Rectangles Similar To Each Other Their lengths are three times their widths. For example, these two rectangles are the same shape but not the same size, so they are similar: Similar shapes are enlargements of each other using a scale factor. Abcd is too short in length to. For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ (. Are All Rectangles Similar To Each Other.
From classfullrequotes.z21.web.core.windows.net
Area Of Rectangles And Squares Are All Rectangles Similar To Each Other All the corresponding angles in the similar. For example, a \ ( 1 \times 2 \) rectangle is not similar to a \ ( 2 \times 3 \) rectangle, even though they both have 4 right angles, since their side lengths have different ratios. Rectangles efgh and ijkl are similar. To determine if the rectangles are similar, set up a. Are All Rectangles Similar To Each Other.