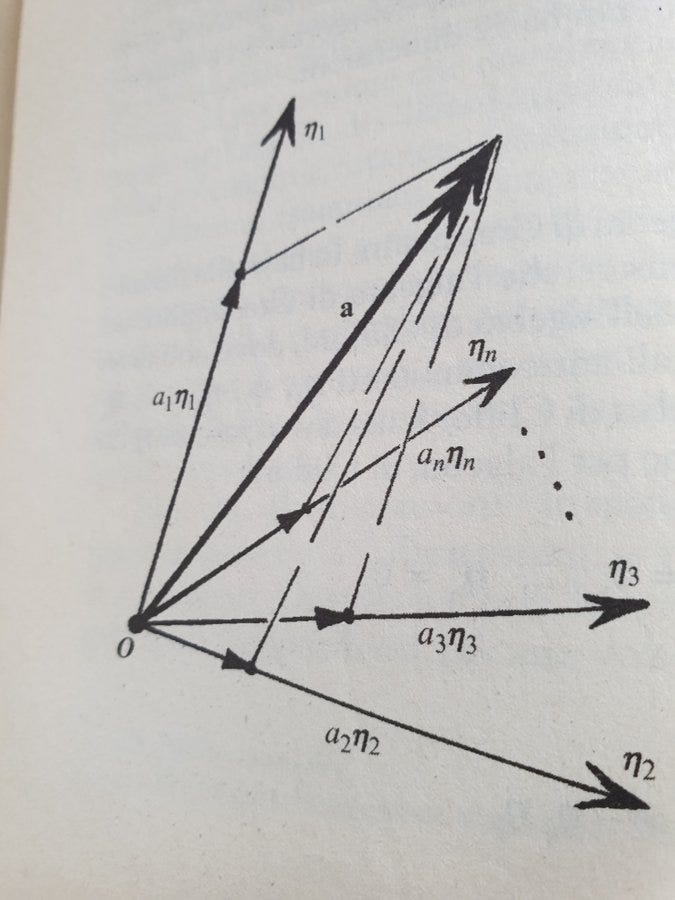
Second Dual Space Definition . It consists of all linear. Set := set of linear functionals on v 0 := zero function [v 7→0 for all v ∈ v ] (f1 + f2)(v) := f1(v) + f2(v) [pointwise. Dual spaces are useful in that they allow us to phrase many important. If you have a vector space, any vector space, you can define linear functions on that space. Given a vector space $v$ over a field $\f$, its dual space, written $v^*$, is the set of all linear maps from $v$ to $\f$. The second dual space of a vector space x, denoted as x**, is the dual space of the dual space x*. The dual space v 0 of v is defined as follows: A set of all linear functions ℒ (v, 𝔽) deserves a special label. The dual space of v, denoted by v *, is the vector space of all linear. Of course, we are now. In these notes we introduce the notion of a dual space.
from medium.com
Dual spaces are useful in that they allow us to phrase many important. Of course, we are now. The second dual space of a vector space x, denoted as x**, is the dual space of the dual space x*. If you have a vector space, any vector space, you can define linear functions on that space. A set of all linear functions ℒ (v, 𝔽) deserves a special label. The dual space v 0 of v is defined as follows: Set := set of linear functionals on v 0 := zero function [v 7→0 for all v ∈ v ] (f1 + f2)(v) := f1(v) + f2(v) [pointwise. The dual space of v, denoted by v *, is the vector space of all linear. In these notes we introduce the notion of a dual space. Given a vector space $v$ over a field $\f$, its dual space, written $v^*$, is the set of all linear maps from $v$ to $\f$.
Understanding dual spaces. Time for a short preparatory post about
Second Dual Space Definition The dual space of v, denoted by v *, is the vector space of all linear. Dual spaces are useful in that they allow us to phrase many important. The dual space v 0 of v is defined as follows: Set := set of linear functionals on v 0 := zero function [v 7→0 for all v ∈ v ] (f1 + f2)(v) := f1(v) + f2(v) [pointwise. If you have a vector space, any vector space, you can define linear functions on that space. Given a vector space $v$ over a field $\f$, its dual space, written $v^*$, is the set of all linear maps from $v$ to $\f$. In these notes we introduce the notion of a dual space. A set of all linear functions ℒ (v, 𝔽) deserves a special label. Of course, we are now. It consists of all linear. The dual space of v, denoted by v *, is the vector space of all linear. The second dual space of a vector space x, denoted as x**, is the dual space of the dual space x*.
From www.researchgate.net
(PDF) Algebraic dual space Second Dual Space Definition Set := set of linear functionals on v 0 := zero function [v 7→0 for all v ∈ v ] (f1 + f2)(v) := f1(v) + f2(v) [pointwise. If you have a vector space, any vector space, you can define linear functions on that space. In these notes we introduce the notion of a dual space. The second dual space. Second Dual Space Definition.
From danielrk.com
RankNullity, Dual Spaces, Strang's Fundamental Subspaces (Linear Maps Second Dual Space Definition Of course, we are now. If you have a vector space, any vector space, you can define linear functions on that space. A set of all linear functions ℒ (v, 𝔽) deserves a special label. It consists of all linear. The dual space v 0 of v is defined as follows: Set := set of linear functionals on v 0. Second Dual Space Definition.
From www.youtube.com
The Double Dual Space Tensors 9 YouTube Second Dual Space Definition The dual space v 0 of v is defined as follows: If you have a vector space, any vector space, you can define linear functions on that space. A set of all linear functions ℒ (v, 𝔽) deserves a special label. Of course, we are now. The dual space of v, denoted by v *, is the vector space of. Second Dual Space Definition.
From www.youtube.com
How To Double Space Lines In Microsoft Word (EASY Tutorial) YouTube Second Dual Space Definition It consists of all linear. If you have a vector space, any vector space, you can define linear functions on that space. The second dual space of a vector space x, denoted as x**, is the dual space of the dual space x*. A set of all linear functions ℒ (v, 𝔽) deserves a special label. Set := set of. Second Dual Space Definition.
From www.youtube.com
Prove that Dual space R^n is R^n. Lecture 28 Functional analysis Second Dual Space Definition Dual spaces are useful in that they allow us to phrase many important. Set := set of linear functionals on v 0 := zero function [v 7→0 for all v ∈ v ] (f1 + f2)(v) := f1(v) + f2(v) [pointwise. The second dual space of a vector space x, denoted as x**, is the dual space of the dual. Second Dual Space Definition.
From www.researchgate.net
Download PDF Dual spaces to Orlicz Lorentz spaces Second Dual Space Definition The dual space of v, denoted by v *, is the vector space of all linear. The dual space v 0 of v is defined as follows: If you have a vector space, any vector space, you can define linear functions on that space. Given a vector space $v$ over a field $\f$, its dual space, written $v^*$, is the. Second Dual Space Definition.
From valuesventure54thcoy.blogspot.com
Double Spaced Example Steps on how to double space or change line Second Dual Space Definition Dual spaces are useful in that they allow us to phrase many important. The second dual space of a vector space x, denoted as x**, is the dual space of the dual space x*. In these notes we introduce the notion of a dual space. If you have a vector space, any vector space, you can define linear functions on. Second Dual Space Definition.
From www.researchgate.net
(PDF) Representations of dual spaces Second Dual Space Definition A set of all linear functions ℒ (v, 𝔽) deserves a special label. If you have a vector space, any vector space, you can define linear functions on that space. Dual spaces are useful in that they allow us to phrase many important. In these notes we introduce the notion of a dual space. The dual space v 0 of. Second Dual Space Definition.
From www.mdpi.com
Sci Free FullText A Concise Tutorial on Functional Analysis for Second Dual Space Definition If you have a vector space, any vector space, you can define linear functions on that space. The second dual space of a vector space x, denoted as x**, is the dual space of the dual space x*. It consists of all linear. The dual space of v, denoted by v *, is the vector space of all linear. A. Second Dual Space Definition.
From medium.com
Understanding dual spaces. Time for a short preparatory post about Second Dual Space Definition The dual space v 0 of v is defined as follows: Of course, we are now. Given a vector space $v$ over a field $\f$, its dual space, written $v^*$, is the set of all linear maps from $v$ to $\f$. A set of all linear functions ℒ (v, 𝔽) deserves a special label. It consists of all linear. Set. Second Dual Space Definition.
From www.youtube.com
Dual Spaces in Linear Algebra and Geometry YouTube Second Dual Space Definition It consists of all linear. Given a vector space $v$ over a field $\f$, its dual space, written $v^*$, is the set of all linear maps from $v$ to $\f$. The second dual space of a vector space x, denoted as x**, is the dual space of the dual space x*. Of course, we are now. A set of all. Second Dual Space Definition.
From www.chegg.com
Solved Problem 15. Let V be a vector space. The double dual Second Dual Space Definition Set := set of linear functionals on v 0 := zero function [v 7→0 for all v ∈ v ] (f1 + f2)(v) := f1(v) + f2(v) [pointwise. The second dual space of a vector space x, denoted as x**, is the dual space of the dual space x*. The dual space v 0 of v is defined as follows:. Second Dual Space Definition.
From www.youtube.com
Hilbert space, its dual and second dual spaces YouTube Second Dual Space Definition Of course, we are now. A set of all linear functions ℒ (v, 𝔽) deserves a special label. If you have a vector space, any vector space, you can define linear functions on that space. The dual space of v, denoted by v *, is the vector space of all linear. Set := set of linear functionals on v 0. Second Dual Space Definition.
From dokumen.tips
(PDF) Dual Spaces DOKUMEN.TIPS Second Dual Space Definition The second dual space of a vector space x, denoted as x**, is the dual space of the dual space x*. It consists of all linear. A set of all linear functions ℒ (v, 𝔽) deserves a special label. If you have a vector space, any vector space, you can define linear functions on that space. The dual space of. Second Dual Space Definition.
From www.researchgate.net
(PDF) Embeddings of finitedimensional operator spaces into the second dual Second Dual Space Definition A set of all linear functions ℒ (v, 𝔽) deserves a special label. The dual space v 0 of v is defined as follows: Given a vector space $v$ over a field $\f$, its dual space, written $v^*$, is the set of all linear maps from $v$ to $\f$. The dual space of v, denoted by v *, is the. Second Dual Space Definition.
From www.youtube.com
Dual Space YouTube Second Dual Space Definition A set of all linear functions ℒ (v, 𝔽) deserves a special label. Set := set of linear functionals on v 0 := zero function [v 7→0 for all v ∈ v ] (f1 + f2)(v) := f1(v) + f2(v) [pointwise. It consists of all linear. Dual spaces are useful in that they allow us to phrase many important. If. Second Dual Space Definition.
From www.youtube.com
DUAL SPACE IN LINEAR ALGEBRA 🔥 YouTube Second Dual Space Definition Of course, we are now. The dual space v 0 of v is defined as follows: Given a vector space $v$ over a field $\f$, its dual space, written $v^*$, is the set of all linear maps from $v$ to $\f$. A set of all linear functions ℒ (v, 𝔽) deserves a special label. The second dual space of a. Second Dual Space Definition.
From www.youtube.com
Dual Basis dual_space Dual Space Vector space Linear Second Dual Space Definition The second dual space of a vector space x, denoted as x**, is the dual space of the dual space x*. In these notes we introduce the notion of a dual space. Dual spaces are useful in that they allow us to phrase many important. Of course, we are now. It consists of all linear. The dual space of v,. Second Dual Space Definition.
From pdodds.w3.uvm.edu
Matrixology (Linear Algebra), Season 8 Second Dual Space Definition A set of all linear functions ℒ (v, 𝔽) deserves a special label. In these notes we introduce the notion of a dual space. Set := set of linear functionals on v 0 := zero function [v 7→0 for all v ∈ v ] (f1 + f2)(v) := f1(v) + f2(v) [pointwise. The second dual space of a vector space. Second Dual Space Definition.
From www.youtube.com
Functional Analysis 22 Dual Spaces YouTube Second Dual Space Definition Set := set of linear functionals on v 0 := zero function [v 7→0 for all v ∈ v ] (f1 + f2)(v) := f1(v) + f2(v) [pointwise. In these notes we introduce the notion of a dual space. The dual space of v, denoted by v *, is the vector space of all linear. It consists of all linear.. Second Dual Space Definition.
From www.youtube.com
Linear functional and Dual Space (Easiest explained Linear Algebra Second Dual Space Definition It consists of all linear. The dual space of v, denoted by v *, is the vector space of all linear. Set := set of linear functionals on v 0 := zero function [v 7→0 for all v ∈ v ] (f1 + f2)(v) := f1(v) + f2(v) [pointwise. Of course, we are now. A set of all linear functions. Second Dual Space Definition.
From www.youtube.com
Dual space Meaning YouTube Second Dual Space Definition Given a vector space $v$ over a field $\f$, its dual space, written $v^*$, is the set of all linear maps from $v$ to $\f$. Set := set of linear functionals on v 0 := zero function [v 7→0 for all v ∈ v ] (f1 + f2)(v) := f1(v) + f2(v) [pointwise. Dual spaces are useful in that they. Second Dual Space Definition.
From www.youtube.com
Conjugate space or Dual space in functional analysis YouTube Second Dual Space Definition Set := set of linear functionals on v 0 := zero function [v 7→0 for all v ∈ v ] (f1 + f2)(v) := f1(v) + f2(v) [pointwise. It consists of all linear. In these notes we introduce the notion of a dual space. A set of all linear functions ℒ (v, 𝔽) deserves a special label. Given a vector. Second Dual Space Definition.
From www.youtube.com
Prove that dual space of l^p is l^q Dual space Functional Second Dual Space Definition The dual space of v, denoted by v *, is the vector space of all linear. Dual spaces are useful in that they allow us to phrase many important. Given a vector space $v$ over a field $\f$, its dual space, written $v^*$, is the set of all linear maps from $v$ to $\f$. The dual space v 0 of. Second Dual Space Definition.
From www.youtube.com
Dual Space of Linear Functionals.wmv YouTube Second Dual Space Definition A set of all linear functions ℒ (v, 𝔽) deserves a special label. If you have a vector space, any vector space, you can define linear functions on that space. Set := set of linear functionals on v 0 := zero function [v 7→0 for all v ∈ v ] (f1 + f2)(v) := f1(v) + f2(v) [pointwise. The dual. Second Dual Space Definition.
From www.researchgate.net
(PDF) An abstract algebraictopological approach to the notions of a Second Dual Space Definition The dual space v 0 of v is defined as follows: Dual spaces are useful in that they allow us to phrase many important. It consists of all linear. In these notes we introduce the notion of a dual space. Of course, we are now. Given a vector space $v$ over a field $\f$, its dual space, written $v^*$, is. Second Dual Space Definition.
From grammar.yourdictionary.com
Do You Need Two Spaces After a Period? There’s Only One Answer Second Dual Space Definition Set := set of linear functionals on v 0 := zero function [v 7→0 for all v ∈ v ] (f1 + f2)(v) := f1(v) + f2(v) [pointwise. Dual spaces are useful in that they allow us to phrase many important. A set of all linear functions ℒ (v, 𝔽) deserves a special label. It consists of all linear. The. Second Dual Space Definition.
From www.youtube.com
Dual Bases and Dual Maps YouTube Second Dual Space Definition If you have a vector space, any vector space, you can define linear functions on that space. Of course, we are now. The second dual space of a vector space x, denoted as x**, is the dual space of the dual space x*. Dual spaces are useful in that they allow us to phrase many important. Set := set of. Second Dual Space Definition.
From www.researchgate.net
(PDF) Complemented Subspaces of PAdic Second Dual Banach Spaces Second Dual Space Definition Dual spaces are useful in that they allow us to phrase many important. Set := set of linear functionals on v 0 := zero function [v 7→0 for all v ∈ v ] (f1 + f2)(v) := f1(v) + f2(v) [pointwise. In these notes we introduce the notion of a dual space. Of course, we are now. The dual space. Second Dual Space Definition.
From www.cfm.brown.edu
Linear Algebra, Part 3 Dual Spaces (Mathematica) Second Dual Space Definition Dual spaces are useful in that they allow us to phrase many important. The dual space v 0 of v is defined as follows: Of course, we are now. If you have a vector space, any vector space, you can define linear functions on that space. The second dual space of a vector space x, denoted as x**, is the. Second Dual Space Definition.
From www.youtube.com
What is a dual vector space? Introduction YouTube Second Dual Space Definition It consists of all linear. The dual space of v, denoted by v *, is the vector space of all linear. Given a vector space $v$ over a field $\f$, its dual space, written $v^*$, is the set of all linear maps from $v$ to $\f$. In these notes we introduce the notion of a dual space. Dual spaces are. Second Dual Space Definition.
From www.youtube.com
Dual space Dual basis Important Theorems YouTube Second Dual Space Definition In these notes we introduce the notion of a dual space. The dual space v 0 of v is defined as follows: Dual spaces are useful in that they allow us to phrase many important. Set := set of linear functionals on v 0 := zero function [v 7→0 for all v ∈ v ] (f1 + f2)(v) := f1(v). Second Dual Space Definition.
From www.studypool.com
SOLUTION Linear algebra 3 dual spaces Studypool Second Dual Space Definition In these notes we introduce the notion of a dual space. The dual space v 0 of v is defined as follows: Given a vector space $v$ over a field $\f$, its dual space, written $v^*$, is the set of all linear maps from $v$ to $\f$. It consists of all linear. If you have a vector space, any vector. Second Dual Space Definition.
From studylib.net
Dual Spaces Second Dual Space Definition The second dual space of a vector space x, denoted as x**, is the dual space of the dual space x*. Dual spaces are useful in that they allow us to phrase many important. It consists of all linear. Set := set of linear functionals on v 0 := zero function [v 7→0 for all v ∈ v ] (f1. Second Dual Space Definition.
From math.stackexchange.com
linear algebra Dual Spaces Isomorphism Mathematics Stack Exchange Second Dual Space Definition A set of all linear functions ℒ (v, 𝔽) deserves a special label. Set := set of linear functionals on v 0 := zero function [v 7→0 for all v ∈ v ] (f1 + f2)(v) := f1(v) + f2(v) [pointwise. It consists of all linear. The dual space of v, denoted by v *, is the vector space of. Second Dual Space Definition.