Triangle Formula Area Sin . Formulas, notes, examples, and practice test (with solutions) topics include. You are familiar with the formula r = 1 2 b h to find the area of a triangle where b is the length of a base of the triangle and h is the height, or the. C is the included angle. Using trigonometry, we can derive an effective formula for finding the area of a triangle, especially when the height is unknown, but you have information about its angles and sides. The most common formula for the area of a triangle would be: You may see this referred to as the. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. Areaδ = ½ ab sin c. Area = ½ × base (b) × height (h) another formula that can be used to obtain the area of a triangle uses the sine function. The area of any triangle can be calculated using the formula: Law of sines, law of cosines, and area of triangles. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate. Finding the area of a triangle using sine.
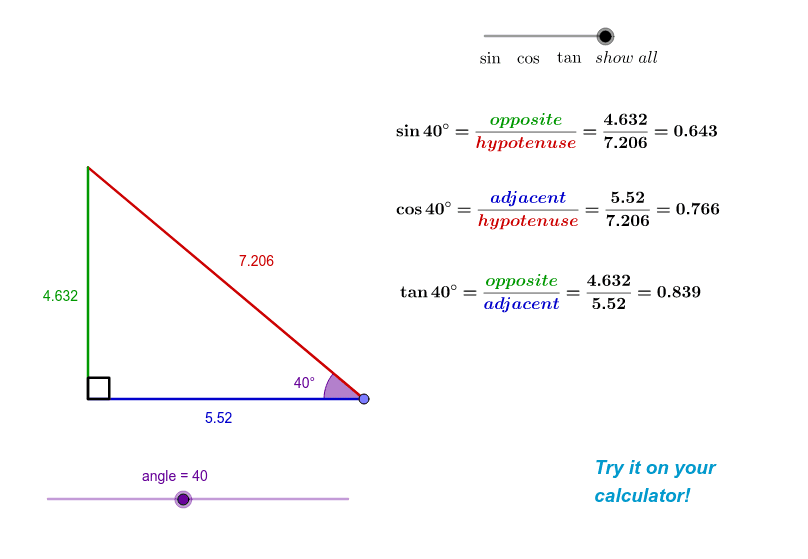
from www.geogebra.org
The most common formula for the area of a triangle would be: C is the included angle. You are familiar with the formula r = 1 2 b h to find the area of a triangle where b is the length of a base of the triangle and h is the height, or the. Areaδ = ½ ab sin c. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate. The area of any triangle can be calculated using the formula: Finding the area of a triangle using sine. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. You may see this referred to as the. Formulas, notes, examples, and practice test (with solutions) topics include.
sin, cos and tan in a right angled triangle GeoGebra
Triangle Formula Area Sin Areaδ = ½ ab sin c. The most common formula for the area of a triangle would be: Areaδ = ½ ab sin c. The area of any triangle can be calculated using the formula: \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate. Area = ½ × base (b) × height (h) another formula that can be used to obtain the area of a triangle uses the sine function. C is the included angle. You may see this referred to as the. Finding the area of a triangle using sine. Formulas, notes, examples, and practice test (with solutions) topics include. Using trigonometry, we can derive an effective formula for finding the area of a triangle, especially when the height is unknown, but you have information about its angles and sides. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. You are familiar with the formula r = 1 2 b h to find the area of a triangle where b is the length of a base of the triangle and h is the height, or the. Law of sines, law of cosines, and area of triangles.
From www.sexiezpix.com
Trigonometry Theorems Formula Rules And Worksheets sexiezpix Porn Triangle Formula Area Sin \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate. The area of any triangle can be calculated using the formula: Areaδ = ½ ab sin c. Using trigonometry, we can derive an effective formula for finding the area of a triangle, especially when the height is unknown, but you have information about its angles. Triangle Formula Area Sin.
From mathsathome.com
How to Find the Area of a Triangle Using the Sine Rule Triangle Formula Area Sin You are familiar with the formula r = 1 2 b h to find the area of a triangle where b is the length of a base of the triangle and h is the height, or the. The area of any triangle can be calculated using the formula: Finding the area of a triangle using sine. Area = ½ ×. Triangle Formula Area Sin.
From mathsathome.com
How to Find the Area of a Triangle Using the Sine Rule Triangle Formula Area Sin Formulas, notes, examples, and practice test (with solutions) topics include. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. Finding the area of a triangle using sine. C is the included angle. The most common formula for the area of a triangle would be: \ (\text {area of. Triangle Formula Area Sin.
From quizizz.com
Section 14 4 Area and The Law of Sines Quizizz Triangle Formula Area Sin You are familiar with the formula r = 1 2 b h to find the area of a triangle where b is the length of a base of the triangle and h is the height, or the. C is the included angle. Using trigonometry, we can derive an effective formula for finding the area of a triangle, especially when the. Triangle Formula Area Sin.
From www.cazoommaths.com
The Sine Rule Worksheet Cazoom Maths Worksheets Triangle Formula Area Sin C is the included angle. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. Law of sines, law of cosines, and area of triangles. Finding the area of a triangle using sine. Area = ½ × base (b) × height (h) another formula that can be used to. Triangle Formula Area Sin.
From jamesleary.blogspot.com
How To Find The Value Of X In A Triangle Sides Calculator James Leary Triangle Formula Area Sin You may see this referred to as the. You are familiar with the formula r = 1 2 b h to find the area of a triangle where b is the length of a base of the triangle and h is the height, or the. Areaδ = ½ ab sin c. C is the included angle. Finding the area of. Triangle Formula Area Sin.
From www.pinterest.com
Trigonometry Sine and Cosine rule. Most schools use SOHCAHTOA and Triangle Formula Area Sin \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate. You may see this referred to as the. You are familiar with the formula r = 1 2 b h to find the area of a triangle where b is the length of a base of the triangle and h is the height, or the.. Triangle Formula Area Sin.
From www.youtube.com
Area of Parallelograms Sine Formula YouTube Triangle Formula Area Sin The most common formula for the area of a triangle would be: Area = ½ × base (b) × height (h) another formula that can be used to obtain the area of a triangle uses the sine function. You may see this referred to as the. You are familiar with the formula r = 1 2 b h to find. Triangle Formula Area Sin.
From www.nagwa.com
Question Video Using The Sine Rule to Calculate Unknown Lengths in a Triangle Formula Area Sin Areaδ = ½ ab sin c. Formulas, notes, examples, and practice test (with solutions) topics include. The area of any triangle can be calculated using the formula: You may see this referred to as the. Area = ½ × base (b) × height (h) another formula that can be used to obtain the area of a triangle uses the sine. Triangle Formula Area Sin.
From mathsathome.com
How to Find the Area of a Triangle Using the Sine Rule Triangle Formula Area Sin C is the included angle. Formulas, notes, examples, and practice test (with solutions) topics include. Using trigonometry, we can derive an effective formula for finding the area of a triangle, especially when the height is unknown, but you have information about its angles and sides. Finding the area of a triangle using sine. You may see this referred to as. Triangle Formula Area Sin.
From www.bat400.com
Section 4 Sine And Cosine Rule Triangle Formula Area Sin Law of sines, law of cosines, and area of triangles. The area of any triangle can be calculated using the formula: Finding the area of a triangle using sine. Areaδ = ½ ab sin c. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate. Formulas, notes, examples, and practice test (with solutions) topics include.. Triangle Formula Area Sin.
From ar.inspiredpencil.com
Sine Formula Triangle Triangle Formula Area Sin The most common formula for the area of a triangle would be: The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. You are familiar with the formula r = 1 2 b h to find the area of a triangle where b is the length of a base. Triangle Formula Area Sin.
From ar.inspiredpencil.com
Sine Formula Triangle Triangle Formula Area Sin The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. The area of any triangle can be calculated using the formula: Finding the area of a triangle using sine. Using trigonometry, we can derive an effective formula for finding the area of a triangle, especially when the height is. Triangle Formula Area Sin.
From www.slideshare.net
11 X1 T04 05 sine rule (2010) Triangle Formula Area Sin The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. C is the included angle. Area = ½ × base (b) × height (h) another formula that can be used to obtain the area of a triangle uses the sine function. Areaδ = ½ ab sin c. Using trigonometry,. Triangle Formula Area Sin.
From www.youtube.com
Area of a triangle using sine YouTube Triangle Formula Area Sin Finding the area of a triangle using sine. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate. Areaδ = ½ ab sin c. The area of any triangle can be calculated using the. Triangle Formula Area Sin.
From www.slideshare.net
Sine rule Triangle Formula Area Sin Areaδ = ½ ab sin c. Area = ½ × base (b) × height (h) another formula that can be used to obtain the area of a triangle uses the sine function. The area of any triangle can be calculated using the formula: You may see this referred to as the. The area of a triangle can be expressed using. Triangle Formula Area Sin.
From owlcation.com
How to Calculate the Sides and Angles of Triangles Using Pythagoras Triangle Formula Area Sin C is the included angle. The most common formula for the area of a triangle would be: You may see this referred to as the. Law of sines, law of cosines, and area of triangles. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. Using trigonometry, we can. Triangle Formula Area Sin.
From www.vrogue.co
Trigonometry Calculate The Area Of Triangle Abc Mathe vrogue.co Triangle Formula Area Sin The area of any triangle can be calculated using the formula: C is the included angle. Formulas, notes, examples, and practice test (with solutions) topics include. Areaδ = ½ ab sin c. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. Area = ½ × base (b) ×. Triangle Formula Area Sin.
From www.nagwa.com
Question Video Using the Sine Rule to Calculate an Unknown Length in a Triangle Formula Area Sin Formulas, notes, examples, and practice test (with solutions) topics include. Finding the area of a triangle using sine. Area = ½ × base (b) × height (h) another formula that can be used to obtain the area of a triangle uses the sine function. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate. C. Triangle Formula Area Sin.
From gantt-chart-excel.com
Download Sine Of An Angle Calculator Gantt Chart Excel Template Triangle Formula Area Sin Using trigonometry, we can derive an effective formula for finding the area of a triangle, especially when the height is unknown, but you have information about its angles and sides. The area of any triangle can be calculated using the formula: Areaδ = ½ ab sin c. Law of sines, law of cosines, and area of triangles. You may see. Triangle Formula Area Sin.
From mathsathome.com
How to Find the Area of a Triangle Using the Sine Rule Triangle Formula Area Sin Law of sines, law of cosines, and area of triangles. The area of any triangle can be calculated using the formula: Areaδ = ½ ab sin c. You are familiar with the formula r = 1 2 b h to find the area of a triangle where b is the length of a base of the triangle and h is. Triangle Formula Area Sin.
From www.slideserve.com
PPT The Sine & Cosine Rule PowerPoint Presentation, free download Triangle Formula Area Sin You may see this referred to as the. The area of any triangle can be calculated using the formula: C is the included angle. Using trigonometry, we can derive an effective formula for finding the area of a triangle, especially when the height is unknown, but you have information about its angles and sides. \ (\text {area of a triangle}. Triangle Formula Area Sin.
From www.youtube.com
Sine Rule for the Area of a Triangle YouTube Triangle Formula Area Sin The area of any triangle can be calculated using the formula: Area = ½ × base (b) × height (h) another formula that can be used to obtain the area of a triangle uses the sine function. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate. You are familiar with the formula r =. Triangle Formula Area Sin.
From owlcation.com
How to Calculate the Sides and Angles of Triangles Owlcation Triangle Formula Area Sin Area = ½ × base (b) × height (h) another formula that can be used to obtain the area of a triangle uses the sine function. \ (\text {area of a triangle} = \frac {1} {2} ab \sin {c}\) to calculate. Using trigonometry, we can derive an effective formula for finding the area of a triangle, especially when the height. Triangle Formula Area Sin.
From www.geogebra.org
sin, cos and tan in a right angled triangle GeoGebra Triangle Formula Area Sin The area of any triangle can be calculated using the formula: Formulas, notes, examples, and practice test (with solutions) topics include. Areaδ = ½ ab sin c. Using trigonometry, we can derive an effective formula for finding the area of a triangle, especially when the height is unknown, but you have information about its angles and sides. Finding the area. Triangle Formula Area Sin.
From ar.inspiredpencil.com
Isosceles Triangle Formula Sides Triangle Formula Area Sin Finding the area of a triangle using sine. Areaδ = ½ ab sin c. The area of any triangle can be calculated using the formula: Using trigonometry, we can derive an effective formula for finding the area of a triangle, especially when the height is unknown, but you have information about its angles and sides. You are familiar with the. Triangle Formula Area Sin.
From www.youtube.com
Finding the Area of a Triangle (Using Sine) YouTube Triangle Formula Area Sin You are familiar with the formula r = 1 2 b h to find the area of a triangle where b is the length of a base of the triangle and h is the height, or the. You may see this referred to as the. The area of a triangle can be expressed using the lengths of two sides and. Triangle Formula Area Sin.
From www.youtube.com
Area of Triangles Using Trig YouTube Triangle Formula Area Sin The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. The most common formula for the area of a triangle would be: Area = ½ × base (b) × height (h) another formula that can be used to obtain the area of a triangle uses the sine function. You. Triangle Formula Area Sin.
From www.youtube.com
Example Determine the Area of a Triangle Using the Sine Function YouTube Triangle Formula Area Sin Formulas, notes, examples, and practice test (with solutions) topics include. Areaδ = ½ ab sin c. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. The area of any triangle can be calculated using the formula: Area = ½ × base (b) × height (h) another formula that. Triangle Formula Area Sin.
From www.vecteezy.com
The area of triangle using sine. Editable vector EPS10 10854289 Vector Triangle Formula Area Sin The most common formula for the area of a triangle would be: Area = ½ × base (b) × height (h) another formula that can be used to obtain the area of a triangle uses the sine function. Using trigonometry, we can derive an effective formula for finding the area of a triangle, especially when the height is unknown, but. Triangle Formula Area Sin.
From thirdspacelearning.com
Area of a Triangle Trig GCSE Maths Steps, Examples & Worksheet Triangle Formula Area Sin Using trigonometry, we can derive an effective formula for finding the area of a triangle, especially when the height is unknown, but you have information about its angles and sides. Finding the area of a triangle using sine. Law of sines, law of cosines, and area of triangles. Area = ½ × base (b) × height (h) another formula that. Triangle Formula Area Sin.
From passyworldofmathematics.com
Lessons Passy's World of Mathematics Mathematics Help Online Page 6 Triangle Formula Area Sin The area of any triangle can be calculated using the formula: Finding the area of a triangle using sine. Areaδ = ½ ab sin c. Law of sines, law of cosines, and area of triangles. Formulas, notes, examples, and practice test (with solutions) topics include. You may see this referred to as the. Using trigonometry, we can derive an effective. Triangle Formula Area Sin.
From www.teachoo.com
Law of Cosine (Cosine Law) with Examples and Proof Teachoo Triangle Formula Area Sin Finding the area of a triangle using sine. Areaδ = ½ ab sin c. You are familiar with the formula r = 1 2 b h to find the area of a triangle where b is the length of a base of the triangle and h is the height, or the. Area = ½ × base (b) × height (h). Triangle Formula Area Sin.
From nickolasknoeroy.blogspot.com
Area of Triangle Sine Rule NickolasknoeRoy Triangle Formula Area Sin Law of sines, law of cosines, and area of triangles. Formulas, notes, examples, and practice test (with solutions) topics include. The area of a triangle can be expressed using the lengths of two sides and the sine of the included angle. The most common formula for the area of a triangle would be: C is the included angle. Using trigonometry,. Triangle Formula Area Sin.
From www.pinterest.com
Proofs of sine rule, cosine rule, area of a triangle Rules, Sines, Gcse Triangle Formula Area Sin The area of any triangle can be calculated using the formula: You may see this referred to as the. Areaδ = ½ ab sin c. Formulas, notes, examples, and practice test (with solutions) topics include. Area = ½ × base (b) × height (h) another formula that can be used to obtain the area of a triangle uses the sine. Triangle Formula Area Sin.