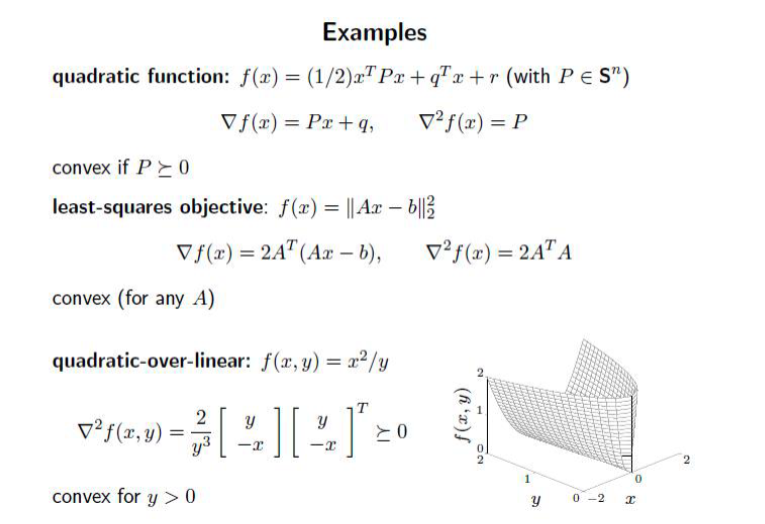
Hessian Quadratic Form . A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. Deriving the gradient and hessian of linear and quadratic functions in matrix notation. Prove that the hessian matrix of a quadratic form $f(x)=x^tax$ is $f^{\prime\prime}(x) = a + a^t$. Nondegenerate critical points are isolated. Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. This tutorial will help you to understand the link between the definiteness of the hessian and the nature of a stationary point. A critical point x 0 2u is non. Hessian of a quadratic function.
from www.chegg.com
Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. This tutorial will help you to understand the link between the definiteness of the hessian and the nature of a stationary point. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. Hessian of a quadratic function. Deriving the gradient and hessian of linear and quadratic functions in matrix notation. Nondegenerate critical points are isolated. A critical point x 0 2u is non. Prove that the hessian matrix of a quadratic form $f(x)=x^tax$ is $f^{\prime\prime}(x) = a + a^t$.
Show the Hessian matrix if the quadratic function
Hessian Quadratic Form Prove that the hessian matrix of a quadratic form $f(x)=x^tax$ is $f^{\prime\prime}(x) = a + a^t$. Prove that the hessian matrix of a quadratic form $f(x)=x^tax$ is $f^{\prime\prime}(x) = a + a^t$. A critical point x 0 2u is non. Deriving the gradient and hessian of linear and quadratic functions in matrix notation. Nondegenerate critical points are isolated. Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. Hessian of a quadratic function. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. This tutorial will help you to understand the link between the definiteness of the hessian and the nature of a stationary point. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point.
From www.researchgate.net
Correction to Harmonic cubic homogeneous polynomials such that the Hessian Quadratic Form Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. A critical point x 0 2u is non. Prove that the hessian matrix of a quadratic form $f(x)=x^tax$ is $f^{\prime\prime}(x) = a + a^t$. Nondegenerate critical points are isolated. Hessian of a quadratic function. The hessian and convexity let f2c2(u);uˆrn. Hessian Quadratic Form.
From jhyun0919.github.io
Geometric Meaning of Hessian Matrix Park's Archive Hessian Quadratic Form The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. Hessian of a quadratic function. Nondegenerate critical points are isolated. A critical point x 0 2u is non. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its. Hessian Quadratic Form.
From www.numerade.com
SOLVED 3.25. Let A be an n x n matrix. Show that the gradient and Hessian Quadratic Form Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. Prove that the hessian matrix of a quadratic form $f(x)=x^tax$ is $f^{\prime\prime}(x) = a + a^t$. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. This tutorial will help you to understand the. Hessian Quadratic Form.
From www.youtube.com
Test 5 For Positive and Negative Definite or SemiDefinite Matrix with Hessian Quadratic Form Deriving the gradient and hessian of linear and quadratic functions in matrix notation. Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. This tutorial will help you to understand the link between the. Hessian Quadratic Form.
From www.youtube.com
Multivariable Calculus Lecture 3 Hessian Matrix Optimization for a Hessian Quadratic Form This tutorial will help you to understand the link between the definiteness of the hessian and the nature of a stationary point. Hessian of a quadratic function. Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. Prove. Hessian Quadratic Form.
From www.algebrapracticeproblems.com
How to calculate the Hessian Matrix (formula and examples) Hessian Quadratic Form This tutorial will help you to understand the link between the definiteness of the hessian and the nature of a stationary point. Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. Prove that the hessian matrix of. Hessian Quadratic Form.
From www.youtube.com
Lecture19.04. Interpreting quadratic terms as a Hessian and gradient Hessian Quadratic Form Nondegenerate critical points are isolated. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. Prove that the hessian matrix of a quadratic form $f(x)=x^tax$ is $f^{\prime\prime}(x) = a + a^t$. Deriving the gradient and hessian of linear and quadratic functions in matrix notation. Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance. Hessian Quadratic Form.
From www.youtube.com
CS540 Lecture 2 Computing Hessian of Quadratic Form Example YouTube Hessian Quadratic Form Hessian of a quadratic function. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. Nondegenerate critical points are isolated. A critical. Hessian Quadratic Form.
From www.slideserve.com
PPT Quadratic Forms and Objective functions with two or more Hessian Quadratic Form Prove that the hessian matrix of a quadratic form $f(x)=x^tax$ is $f^{\prime\prime}(x) = a + a^t$. Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. Deriving the gradient and hessian of linear and quadratic functions in matrix. Hessian Quadratic Form.
From www.slideserve.com
PPT Constrained Optimization PowerPoint Presentation, free download Hessian Quadratic Form Hessian of a quadratic function. This tutorial will help you to understand the link between the definiteness of the hessian and the nature of a stationary point. Deriving the gradient and hessian of linear and quadratic functions in matrix notation. Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the.. Hessian Quadratic Form.
From www.numerade.com
SOLVED You don't have to do E8.8 E8.7 Consider the following quadratic Hessian Quadratic Form A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. Deriving the gradient and hessian of linear and quadratic functions in matrix notation. Nondegenerate critical points are isolated. A critical point x 0 2u is non. Hessian of a quadratic function. This tutorial will help you to understand the link between the definiteness of. Hessian Quadratic Form.
From www.pdfprof.com
hessian is a non symmetric matrix Hessian Quadratic Form Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. Hessian of a quadratic function. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. Deriving the gradient and hessian of linear and quadratic functions in matrix notation. A critical point x 0 2u. Hessian Quadratic Form.
From demonstrations.wolfram.com
Wolfram Demonstrations Project Hessian Quadratic Form Nondegenerate critical points are isolated. A critical point x 0 2u is non. Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. Hessian of a quadratic function. Prove that the hessian matrix of. Hessian Quadratic Form.
From www.youtube.com
Optimization of Quadratic Forms Lecture Part 2 Definite Symmetric Hessian Quadratic Form This tutorial will help you to understand the link between the definiteness of the hessian and the nature of a stationary point. Prove that the hessian matrix of a quadratic form $f(x)=x^tax$ is $f^{\prime\prime}(x) = a + a^t$. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its. Hessian Quadratic Form.
From slideplayer.com
Performance Surfaces. ppt download Hessian Quadratic Form Nondegenerate critical points are isolated. Hessian of a quadratic function. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. Deriving the gradient and hessian of linear and quadratic functions in matrix notation. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. A critical point x 0 2u is non. This. Hessian Quadratic Form.
From www.numerade.com
SOLVEDGiven the following quadratic forms, construct the bordered Hessian Quadratic Form A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. This tutorial will help you to understand the link between the definiteness of the hessian and the nature of a stationary point. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. Given a matrix \ (a\) of \ (n\) demeaned data. Hessian Quadratic Form.
From www.numerade.com
SOLVED Problem 8(A) [10 marks] This problem is concerned with the Hessian Quadratic Form This tutorial will help you to understand the link between the definiteness of the hessian and the nature of a stationary point. Hessian of a quadratic function. Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. Nondegenerate critical points are isolated. Prove that the hessian matrix of a quadratic. Hessian Quadratic Form.
From slideplayer.com
Performance Surfaces. ppt download Hessian Quadratic Form Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. Nondegenerate critical points are isolated. Hessian of a quadratic function. Deriving the gradient and hessian of linear and quadratic functions in matrix notation. A. Hessian Quadratic Form.
From machinelearningmastery.com
A Gentle Introduction To Hessian Matrices Hessian Quadratic Form Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. Prove that the hessian matrix of a quadratic form $f(x)=x^tax$ is $f^{\prime\prime}(x) = a + a^t$. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. Deriving the gradient and hessian of linear and. Hessian Quadratic Form.
From www.researchgate.net
Form of the Hessian H(x, ¯ θ) for the quadratic approximation (6) with Hessian Quadratic Form Hessian of a quadratic function. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. Deriving the gradient and hessian of linear and quadratic functions in matrix notation. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. Nondegenerate critical points are isolated. Given a matrix \ (a\) of \ (n\) demeaned. Hessian Quadratic Form.
From gistlib.com
gistlib calculate hessian normal form in matlab Hessian Quadratic Form The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. Prove that the hessian matrix of a quadratic form $f(x)=x^tax$ is $f^{\prime\prime}(x) = a + a^t$. This tutorial will help you to understand the link between the definiteness of the hessian and. Hessian Quadratic Form.
From www.researchgate.net
(PDF) A concise formula for the Hessian determinant of a function Hessian Quadratic Form This tutorial will help you to understand the link between the definiteness of the hessian and the nature of a stationary point. Nondegenerate critical points are isolated. Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. Hessian of a quadratic function. The hessian and convexity let f2c2(u);uˆrn open, x. Hessian Quadratic Form.
From www.slideserve.com
PPT Quadratic Forms and Objective functions with two or more Hessian Quadratic Form Deriving the gradient and hessian of linear and quadratic functions in matrix notation. Prove that the hessian matrix of a quadratic form $f(x)=x^tax$ is $f^{\prime\prime}(x) = a + a^t$. Hessian of a quadratic function. A critical point x 0 2u is non. Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\). Hessian Quadratic Form.
From www.numerade.com
SOLVED m 6 Suppose that the Hessian matrix of a certain quadratic Hessian Quadratic Form This tutorial will help you to understand the link between the definiteness of the hessian and the nature of a stationary point. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. Deriving the gradient and hessian of linear and quadratic functions. Hessian Quadratic Form.
From slideplayer.com
Performance Surfaces. ppt download Hessian Quadratic Form This tutorial will help you to understand the link between the definiteness of the hessian and the nature of a stationary point. Hessian of a quadratic function. Prove that the hessian matrix of a quadratic form $f(x)=x^tax$ is $f^{\prime\prime}(x) = a + a^t$. Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n. Hessian Quadratic Form.
From www.slideserve.com
PPT QSD Quadratic Shape Descriptors PowerPoint Presentation, free Hessian Quadratic Form Hessian of a quadratic function. This tutorial will help you to understand the link between the definiteness of the hessian and the nature of a stationary point. Nondegenerate critical points are isolated. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. A critical point x 0 2u is non. Given a matrix \ (a\) of \ (n\). Hessian Quadratic Form.
From math.stackexchange.com
multivariable calculus Gradient and Hessian of the product of two Hessian Quadratic Form A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. Hessian of a quadratic function. Nondegenerate critical points are isolated. Deriving the gradient and hessian of linear and quadratic functions in matrix notation. Prove that the hessian matrix of a quadratic form $f(x)=x^tax$ is $f^{\prime\prime}(x) = a + a^t$. A critical point x 0. Hessian Quadratic Form.
From www.researchgate.net
Harmonic cubic homogeneous polynomials such that the normsquared of Hessian Quadratic Form Prove that the hessian matrix of a quadratic form $f(x)=x^tax$ is $f^{\prime\prime}(x) = a + a^t$. Hessian of a quadratic function. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. This tutorial will help you to understand the link between the definiteness of the hessian and the nature of a stationary point. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is. Hessian Quadratic Form.
From es.scribd.com
Quadratic Forms and Hessian Matrix PDF PDF Conjunto convexo Hessian Quadratic Form A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. Nondegenerate critical points are isolated. Prove that the hessian matrix of a quadratic form $f(x)=x^tax$ is $f^{\prime\prime}(x) = a + a^t$. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. Deriving the gradient and hessian of linear and quadratic functions in. Hessian Quadratic Form.
From demonstrations.wolfram.com
Wolfram Demonstrations Project Hessian Quadratic Form A critical point x 0 2u is non. This tutorial will help you to understand the link between the definiteness of the hessian and the nature of a stationary point. Hessian of a quadratic function. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. Given a matrix \ (a\) of \ (n\) demeaned. Hessian Quadratic Form.
From www.youtube.com
Preliminaries The Gradient and the Hessian; Quadratic Functions YouTube Hessian Quadratic Form A critical point x 0 2u is non. This tutorial will help you to understand the link between the definiteness of the hessian and the nature of a stationary point. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. Hessian of a quadratic function. Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric. Hessian Quadratic Form.
From www.youtube.com
Hessian matrix as a bilinear form that outputs secondorder directional Hessian Quadratic Form A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. Nondegenerate critical points are isolated. A critical point x 0 2u is non. Prove that the hessian matrix of a quadratic form $f(x)=x^tax$ is $f^{\prime\prime}(x) = a + a^t$. Deriving the gradient. Hessian Quadratic Form.
From www.pinterest.at
Hessian matrix and quadratic approximation, with example in Python Hessian Quadratic Form Nondegenerate critical points are isolated. Prove that the hessian matrix of a quadratic form $f(x)=x^tax$ is $f^{\prime\prime}(x) = a + a^t$. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. A critical point x 0 2u is non. This tutorial will help you to understand the link between the definiteness of the hessian. Hessian Quadratic Form.
From www.chegg.com
Show the Hessian matrix if the quadratic function Hessian Quadratic Form A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. The hessian and convexity let f2c2(u);uˆrn open, x 0 2ua critical point. A critical point x 0 2u is non. Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. Hessian of a quadratic. Hessian Quadratic Form.
From www.youtube.com
Linear Algebra Hessian Matrix YouTube Hessian Quadratic Form Nondegenerate critical points are isolated. A critical point x 0 2u is non. Given a matrix \ (a\) of \ (n\) demeaned data points, the symmetric covariance matrix \ (c=\frac1n aa^t\) determines the. Hessian of a quadratic function. A quadratic form $h:\mathbb{r}^n\to\mathbb{r}$ is a function such that its value in a vector $v =. The hessian and convexity let f2c2(u);uˆrn. Hessian Quadratic Form.