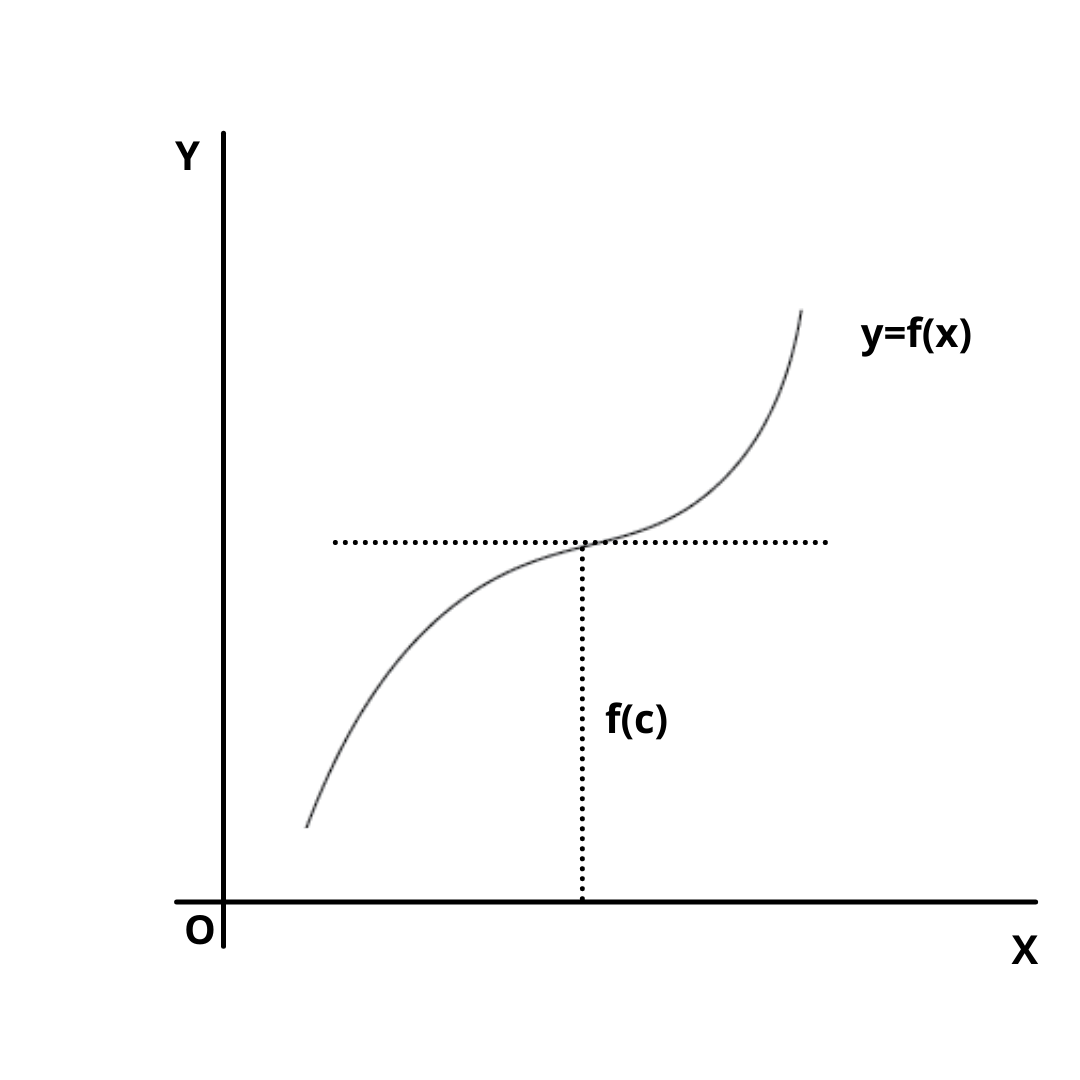
Point Of Inflection Wiki . an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. the point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the end of a range of strict convexity upwards and the end of a. maxima and minima are points where a function reaches a highest or lowest value, respectively. to find inflection points, start by differentiating your function to find the. There are two kinds of. a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides of the stationary. in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and.
from mathemerize.com
to find inflection points, start by differentiating your function to find the. There are two kinds of. a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides of the stationary. maxima and minima are points where a function reaches a highest or lowest value, respectively. in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and. the point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the end of a range of strict convexity upwards and the end of a. an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes.
What is the Point of Inflection ? Mathemerize
Point Of Inflection Wiki to find inflection points, start by differentiating your function to find the. a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides of the stationary. in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and. maxima and minima are points where a function reaches a highest or lowest value, respectively. There are two kinds of. to find inflection points, start by differentiating your function to find the. the point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the end of a range of strict convexity upwards and the end of a. an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes.
From www.radfordmathematics.com
Point of Inflection Calculus Point Of Inflection Wiki maxima and minima are points where a function reaches a highest or lowest value, respectively. in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and. a falling point of inflection (or inflexion) is one where the derivative of the function is negative on. Point Of Inflection Wiki.
From collegedunia.com
Inflection Point Calculus, Graph & Concavity Point Of Inflection Wiki There are two kinds of. an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. to find inflection points, start by differentiating your function to find the. the point $ x _ {0} $ is called a point of inflection for $ f $ if it is. Point Of Inflection Wiki.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Wiki maxima and minima are points where a function reaches a highest or lowest value, respectively. a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides of the stationary. in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both. Point Of Inflection Wiki.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Wiki to find inflection points, start by differentiating your function to find the. There are two kinds of. a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides of the stationary. in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\). Point Of Inflection Wiki.
From www.linstitute.net
IB DP Maths AI HL复习笔记5.2.6 Concavity & Points of Inflection翰林国际教育 Point Of Inflection Wiki an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. There are two kinds of. to find inflection points, start by differentiating your function to find the. the point $ x _ {0} $ is called a point of inflection for $ f $ if it is. Point Of Inflection Wiki.
From mathemerize.com
What is the Point of Inflection ? Mathemerize Point Of Inflection Wiki the point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the end of a range of strict convexity upwards and the end of a. in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\). Point Of Inflection Wiki.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Wiki maxima and minima are points where a function reaches a highest or lowest value, respectively. to find inflection points, start by differentiating your function to find the. an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. There are two kinds of. in typical problems, we. Point Of Inflection Wiki.
From www.youtube.com
Point of inflection and point of inflexion YouTube Point Of Inflection Wiki to find inflection points, start by differentiating your function to find the. an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and. . Point Of Inflection Wiki.
From www.storyofmathematics.com
Inflection Points Calculator + Online Solver With Free Steps Point Of Inflection Wiki to find inflection points, start by differentiating your function to find the. a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides of the stationary. the point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the. Point Of Inflection Wiki.
From www.researchgate.net
Pictorial representation of inflection1 approach considering one Point Of Inflection Wiki There are two kinds of. the point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the end of a range of strict convexity upwards and the end of a. maxima and minima are points where a function reaches a highest or lowest value, respectively. an inflection. Point Of Inflection Wiki.
From www.youtube.com
Point of Inflection Point of Inflexion f''(x)=0 Definition How Point Of Inflection Wiki to find inflection points, start by differentiating your function to find the. a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides of the stationary. the point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the. Point Of Inflection Wiki.
From mungfali.com
Question Video Finding The 푥coordinates Of The Inflection Points Of A 168 Point Of Inflection Wiki a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides of the stationary. There are two kinds of. in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and. maxima and minima are points. Point Of Inflection Wiki.
From www.youtube.com
Inflexion Point YouTube Point Of Inflection Wiki an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and. to find inflection points, start by differentiating your function to find the. . Point Of Inflection Wiki.
From www.youtube.com
Point of Inflection YouTube Point Of Inflection Wiki in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and. There are two kinds of. maxima and minima are points where a function reaches a highest or lowest value, respectively. to find inflection points, start by differentiating your function to find the. . Point Of Inflection Wiki.
From mungfali.com
How To Find Inflection Points Of A Function Point Of Inflection Wiki in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and. a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides of the stationary. an inflection point is a point on a curve at. Point Of Inflection Wiki.
From www.wikihow.com
5 Ways to Find Inflection Points wikiHow Point Of Inflection Wiki an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and. a falling point of inflection (or inflexion) is one where the derivative of. Point Of Inflection Wiki.
From www.nagwa.com
Question Video Finding the Inflection Point of a Function Nagwa Point Of Inflection Wiki maxima and minima are points where a function reaches a highest or lowest value, respectively. in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and. to find inflection points, start by differentiating your function to find the. a falling point of inflection. Point Of Inflection Wiki.
From www.wikihow.com
How to Find Inflection Points 8 Steps wikiHow Point Of Inflection Wiki in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and. the point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the end of a range of strict convexity upwards and the end of. Point Of Inflection Wiki.
From www.thetechedvocate.org
How to calculate inflection point The Tech Edvocate Point Of Inflection Wiki maxima and minima are points where a function reaches a highest or lowest value, respectively. a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides of the stationary. the point $ x _ {0} $ is called a point of inflection for $ f $ if it. Point Of Inflection Wiki.
From www.youtube.com
Inflection Points YouTube Point Of Inflection Wiki in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and. the point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the end of a range of strict convexity upwards and the end of. Point Of Inflection Wiki.
From study.com
Finding Inflection Points and Concavity Overview & Examples Lesson Point Of Inflection Wiki the point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the end of a range of strict convexity upwards and the end of a. There are two kinds of. to find inflection points, start by differentiating your function to find the. an inflection point is a. Point Of Inflection Wiki.
From www.neurochispas.com
Puntos de inflexión de una función Fórmulas y Ejercicios Neurochispas Point Of Inflection Wiki to find inflection points, start by differentiating your function to find the. a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides of the stationary. the point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the. Point Of Inflection Wiki.
From calcworkshop.com
The Second Derivative Test (HowTo w/ 15 StepbyStep Examples!) Point Of Inflection Wiki There are two kinds of. a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides of the stationary. to find inflection points, start by differentiating your function to find the. the point $ x _ {0} $ is called a point of inflection for $ f $. Point Of Inflection Wiki.
From www.radfordmathematics.com
Point of Inflection Calculus Point Of Inflection Wiki the point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the end of a range of strict convexity upwards and the end of a. a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides of the stationary.. Point Of Inflection Wiki.
From www.youtube.com
Finding Points of Inflection and Intervals of Concavity Calculus Point Of Inflection Wiki an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. to find inflection points, start by differentiating your function to find the. There are two kinds of. a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides. Point Of Inflection Wiki.
From statusq.org
Reflections on Inflections StatusQ Point Of Inflection Wiki a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides of the stationary. the point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the end of a range of strict convexity upwards and the end of a.. Point Of Inflection Wiki.
From www.linstitute.net
AQA A Level Maths Pure复习笔记7.4.2 Points of Inflection翰林国际教育 Point Of Inflection Wiki the point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the end of a range of strict convexity upwards and the end of a. to find inflection points, start by differentiating your function to find the. a falling point of inflection (or inflexion) is one where. Point Of Inflection Wiki.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Wiki to find inflection points, start by differentiating your function to find the. There are two kinds of. an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. the point $ x _ {0} $ is called a point of inflection for $ f $ if it is. Point Of Inflection Wiki.
From www.dreamstime.com
Inflection Point on Graph of Function. Stock Vector Illustration of Point Of Inflection Wiki There are two kinds of. the point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the end of a range of strict convexity upwards and the end of a. in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are. Point Of Inflection Wiki.
From roger-well-sullivan.blogspot.com
How to Find Inflection Points Point Of Inflection Wiki There are two kinds of. to find inflection points, start by differentiating your function to find the. the point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the end of a range of strict convexity upwards and the end of a. in typical problems, we find. Point Of Inflection Wiki.
From www.shutterstock.com
Inflection Point On Graph Function Vector Stock Vector (Royalty Free Point Of Inflection Wiki in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and. an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. the point $ x _ {0} $ is called a point of inflection. Point Of Inflection Wiki.
From dxozqnqwl.blob.core.windows.net
Point Of Inflection Using Second Derivative at Gary Jones blog Point Of Inflection Wiki There are two kinds of. an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. the point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the end of a range of strict convexity upwards and the end. Point Of Inflection Wiki.
From dxosemook.blob.core.windows.net
Point Of Inflection Hydrograph at Lisa Williams blog Point Of Inflection Wiki There are two kinds of. a falling point of inflection (or inflexion) is one where the derivative of the function is negative on both sides of the stationary. in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and. the point $ x _. Point Of Inflection Wiki.
From es.other.wiki
Punto de inflexión Inflection point other.wiki Point Of Inflection Wiki to find inflection points, start by differentiating your function to find the. There are two kinds of. maxima and minima are points where a function reaches a highest or lowest value, respectively. in typical problems, we find a function's inflection point by using \(f''=0\) \((\)provided that \(f\) and \(f'\) are both differentiable at that point\()\) and. . Point Of Inflection Wiki.
From www.nagwa.com
Lesson Convexity and Points of Inflection Nagwa Point Of Inflection Wiki There are two kinds of. the point $ x _ {0} $ is called a point of inflection for $ f $ if it is simultaneously the end of a range of strict convexity upwards and the end of a. to find inflection points, start by differentiating your function to find the. a falling point of inflection. Point Of Inflection Wiki.