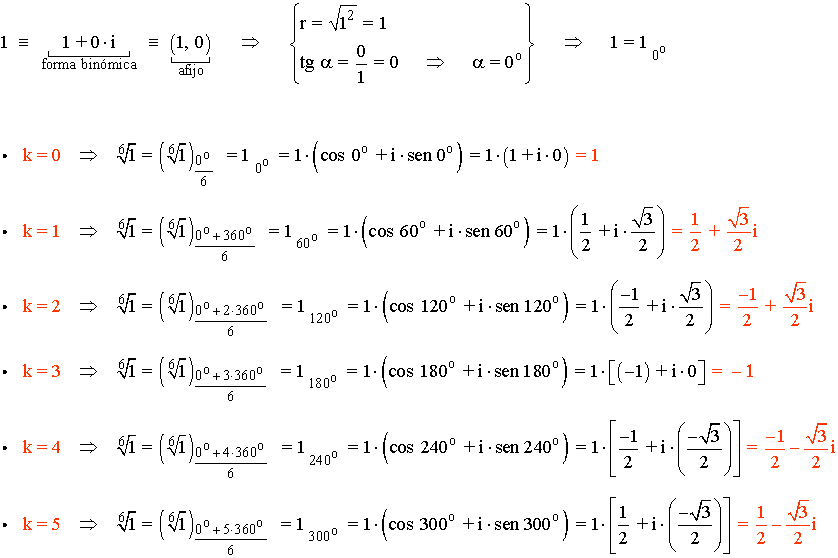Como Despejar Z En Numeros Complejos . Si z=a+bi y w=c+di z+w = (a+bi) + (c+di) = (a+c)+(b+d)i. En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. Sabemos que la tangente no está definida en 90 o y 270 o. En primer lugar pasamos el número complejo a forma polar: Los números complejos pueden sumarse coordenada a coordenada. Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. En este capítulo mostraremos los números complejos, e introduciremos los principales. Como el afijo de z es. Despejando la incógnita z obtenemos que:
from calculo.cc
Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. Si z=a+bi y w=c+di z+w = (a+bi) + (c+di) = (a+c)+(b+d)i. En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. En primer lugar pasamos el número complejo a forma polar: Los números complejos pueden sumarse coordenada a coordenada. Como el afijo de z es. Despejando la incógnita z obtenemos que: Sabemos que la tangente no está definida en 90 o y 270 o. En este capítulo mostraremos los números complejos, e introduciremos los principales.
Ejercicios resueltos de ecuaciones y sistemas con números complejos.
Como Despejar Z En Numeros Complejos En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. Despejando la incógnita z obtenemos que: En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. Como el afijo de z es. En primer lugar pasamos el número complejo a forma polar: Los números complejos pueden sumarse coordenada a coordenada. Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. Si z=a+bi y w=c+di z+w = (a+bi) + (c+di) = (a+c)+(b+d)i. Sabemos que la tangente no está definida en 90 o y 270 o. En este capítulo mostraremos los números complejos, e introduciremos los principales.
From www.youtube.com
NUMEROS COMPLEJOS en CIRCUITOS ELECTRICOS en AC 3 EJERCICIOS Como Despejar Z En Numeros Complejos En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. Si z=a+bi y w=c+di z+w = (a+bi) + (c+di) = (a+c)+(b+d)i.. Como Despejar Z En Numeros Complejos.
From www.aiophotoz.com
Forma Trigonometrica De Un Numero Complejo Ejemplos Colección De Como Despejar Z En Numeros Complejos Como el afijo de z es. En primer lugar pasamos el número complejo a forma polar: En este capítulo mostraremos los números complejos, e introduciremos los principales. Si z=a+bi y w=c+di z+w = (a+bi) + (c+di) = (a+c)+(b+d)i. Sabemos que la tangente no está definida en 90 o y 270 o. Los números complejos pueden sumarse coordenada a coordenada. Los. Como Despejar Z En Numeros Complejos.
From www.youtube.com
Como resolver hacer ecuaciones exponenciales Números complejos con x en Como Despejar Z En Numeros Complejos Los números complejos pueden sumarse coordenada a coordenada. Sabemos que la tangente no está definida en 90 o y 270 o. Despejando la incógnita z obtenemos que: Como el afijo de z es. En este capítulo mostraremos los números complejos, e introduciremos los principales. Los números complejos se basan en la idea de poder definir el número i (llamado unidad. Como Despejar Z En Numeros Complejos.
From www.hotizasexy.com
Gráfica Magnitud Y Conjugado De Números Complejos Youtube Free Nude Como Despejar Z En Numeros Complejos Los números complejos pueden sumarse coordenada a coordenada. Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. En primer lugar pasamos el número complejo a forma polar: En este capítulo mostraremos los números complejos, e introduciremos los principales. Si z=a+bi y w=c+di z+w = (a+bi) +. Como Despejar Z En Numeros Complejos.
From brainly.lat
Realiza las operaciones con los siguientes números complejos Z1 = 74i Como Despejar Z En Numeros Complejos En primer lugar pasamos el número complejo a forma polar: Los números complejos pueden sumarse coordenada a coordenada. En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. En este capítulo mostraremos los números complejos, e introduciremos los principales. Si z=a+bi y w=c+di z+w. Como Despejar Z En Numeros Complejos.
From www.crmefsm.ac.ma
Vueltas y vueltas enjuague portátil numeros complejos elevados a una Como Despejar Z En Numeros Complejos Como el afijo de z es. Si z=a+bi y w=c+di z+w = (a+bi) + (c+di) = (a+c)+(b+d)i. Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. Los números complejos pueden sumarse coordenada a coordenada. En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas. Como Despejar Z En Numeros Complejos.
From www.youtube.com
Norma y conjugado de un número complejo. Parte 3.wmv YouTube Como Despejar Z En Numeros Complejos En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. Los números complejos pueden sumarse coordenada a coordenada. En este capítulo. Como Despejar Z En Numeros Complejos.
From www.aiophotoz.com
Como Resolver Ecuaciones Con Logaritmos Neperianos Ambos Lados Con Como Despejar Z En Numeros Complejos Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. En primer lugar pasamos el número complejo a forma polar: Como el afijo de z es. Los números complejos pueden sumarse coordenada a coordenada. En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con. Como Despejar Z En Numeros Complejos.
From www.youtube.com
CÓMO resolver ECUACIONES con NÚMEROS COMPLEJOS y NÚMEROS IMAGINARIOS Como Despejar Z En Numeros Complejos Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. Los números complejos pueden sumarse coordenada a coordenada. Sabemos que la tangente no está definida en 90 o y 270 o. En primer lugar pasamos el número complejo a forma polar: En este artículo, exploraremos la resolución. Como Despejar Z En Numeros Complejos.
From brainly.lat
1. Considerando los números complejos z = 2 + i, yw = 10 + 4i Como Despejar Z En Numeros Complejos Despejando la incógnita z obtenemos que: En este capítulo mostraremos los números complejos, e introduciremos los principales. Los números complejos pueden sumarse coordenada a coordenada. Sabemos que la tangente no está definida en 90 o y 270 o. Si z=a+bi y w=c+di z+w = (a+bi) + (c+di) = (a+c)+(b+d)i. En primer lugar pasamos el número complejo a forma polar: Como. Como Despejar Z En Numeros Complejos.
From www.studocu.com
23 agosto Definiciones TI Numeros Complejos Unidad I Números Como Despejar Z En Numeros Complejos Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. Como el afijo de z es. En este capítulo mostraremos los números complejos, e introduciremos los principales. Sabemos que la tangente no está definida en 90 o y 270 o. En este artículo, exploraremos la resolución de. Como Despejar Z En Numeros Complejos.
From www.youtube.com
Resolver Ecuaciones con Números Complejos Como Despejar Ecuaciones Como Despejar Z En Numeros Complejos Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. Sabemos que la tangente no está definida en 90 o y 270 o. Los números complejos pueden sumarse coordenada a coordenada. En este capítulo mostraremos los números complejos, e introduciremos los principales. Como el afijo de z. Como Despejar Z En Numeros Complejos.
From calculo.cc
Ejercicios resueltos de factorización y simplificación de números Como Despejar Z En Numeros Complejos Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. En este capítulo mostraremos los números complejos, e introduciremos los principales. En primer lugar pasamos el número complejo a forma polar: Como el afijo de z es. Despejando la incógnita z obtenemos que: Los números complejos pueden. Como Despejar Z En Numeros Complejos.
From diezenmatematicas.jimdofree.com
Despeje de ecuaciones 2 Diez en Matemáticas Como Despejar Z En Numeros Complejos Como el afijo de z es. Sabemos que la tangente no está definida en 90 o y 270 o. En primer lugar pasamos el número complejo a forma polar: Si z=a+bi y w=c+di z+w = (a+bi) + (c+di) = (a+c)+(b+d)i. Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz. Como Despejar Z En Numeros Complejos.
From www.youtube.com
Ecuaciones con Números Complejos YouTube Como Despejar Z En Numeros Complejos En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. Como el afijo de z es. Sabemos que la tangente no. Como Despejar Z En Numeros Complejos.
From apolonio.es
¿Qué es Z en números complejos? Apolonio.es Como Despejar Z En Numeros Complejos Los números complejos pueden sumarse coordenada a coordenada. Sabemos que la tangente no está definida en 90 o y 270 o. Despejando la incógnita z obtenemos que: Como el afijo de z es. Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. En este artículo, exploraremos. Como Despejar Z En Numeros Complejos.
From www.vrogue.co
Como Despejar Una Variable Con Logaritmo Natural Ecua vrogue.co Como Despejar Z En Numeros Complejos En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. Despejando la incógnita z obtenemos que: Sabemos que la tangente no. Como Despejar Z En Numeros Complejos.
From www.youtube.com
Resolver Ecuaciones con Números Complejos Grado 3 Despejar Ecuaciones Como Despejar Z En Numeros Complejos En este capítulo mostraremos los números complejos, e introduciremos los principales. Los números complejos pueden sumarse coordenada a coordenada. Despejando la incógnita z obtenemos que: Como el afijo de z es. En primer lugar pasamos el número complejo a forma polar: Si z=a+bi y w=c+di z+w = (a+bi) + (c+di) = (a+c)+(b+d)i. Los números complejos se basan en la idea. Como Despejar Z En Numeros Complejos.
From store-guccifactory.blogspot.com
Numeros Complejos Con Fracciones Gufa Como Despejar Z En Numeros Complejos En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. Sabemos que la tangente no está definida en 90 o y 270 o. Los números complejos pueden sumarse coordenada a coordenada. Como el afijo de z es. En primer lugar pasamos el número complejo. Como Despejar Z En Numeros Complejos.
From www.youtube.com
Como resolver ecuaciones de segundo grado con números complejos hallar Como Despejar Z En Numeros Complejos Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. En este capítulo mostraremos los números complejos, e introduciremos los principales. Si z=a+bi y w=c+di z+w = (a+bi) + (c+di) = (a+c)+(b+d)i. Despejando la incógnita z obtenemos que: En este artículo, exploraremos la resolución de ecuaciones lineales,. Como Despejar Z En Numeros Complejos.
From sp.lagroup.edu.vn
Resumen de 16 artículos como despejar ecuaciones [actualizado Como Despejar Z En Numeros Complejos Sabemos que la tangente no está definida en 90 o y 270 o. Despejando la incógnita z obtenemos que: Los números complejos pueden sumarse coordenada a coordenada. En este capítulo mostraremos los números complejos, e introduciremos los principales. Como el afijo de z es. En primer lugar pasamos el número complejo a forma polar: Si z=a+bi y w=c+di z+w =. Como Despejar Z En Numeros Complejos.
From www.youtube.com
4. NÚMEROS COMPLEJOS INDICA LA PARTE REAL E IMAGINARIA DE LOS Como Despejar Z En Numeros Complejos En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. Como el afijo de z es. En este capítulo mostraremos los números complejos, e introduciremos los principales. Si z=a+bi y w=c+di z+w = (a+bi) + (c+di) = (a+c)+(b+d)i. Los números complejos se basan en. Como Despejar Z En Numeros Complejos.
From www.tpsearchtool.com
Matematicas Faciles Clasificacion De Los Numeros Complejos Images Como Despejar Z En Numeros Complejos En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. Despejando la incógnita z obtenemos que: Como el afijo de z es. Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal. Como Despejar Z En Numeros Complejos.
From es.slideshare.net
Ecuaciones en números complejos Como Despejar Z En Numeros Complejos En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. En primer lugar pasamos el número complejo a forma polar: Despejando la incógnita z obtenemos que: Sabemos que la tangente no está definida en 90 o y 270 o. Como el afijo de z. Como Despejar Z En Numeros Complejos.
From www.youtube.com
Gráfico de números complejos en el plano complejo YouTube Como Despejar Z En Numeros Complejos En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. Si z=a+bi y w=c+di z+w = (a+bi) + (c+di) = (a+c)+(b+d)i. Como el afijo de z es. Los números complejos pueden sumarse coordenada a coordenada. En primer lugar pasamos el número complejo a forma. Como Despejar Z En Numeros Complejos.
From unejemplosencillo.com
Quais São Os Números Imaginários E Complejos? Ejemplo Sencillo Como Despejar Z En Numeros Complejos Como el afijo de z es. En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. Despejando la incógnita z obtenemos que: Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal. Como Despejar Z En Numeros Complejos.
From www.youtube.com
03 Forma binómica de los números complejos YouTube Como Despejar Z En Numeros Complejos Los números complejos pueden sumarse coordenada a coordenada. Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. Si z=a+bi y w=c+di z+w = (a+bi) + (c+di) = (a+c)+(b+d)i. Despejando la incógnita z obtenemos que: Como el afijo de z es. Sabemos que la tangente no está. Como Despejar Z En Numeros Complejos.
From www.youtube.com
Resolver ecuaciones lineales Aprende a despejar la incógnita YouTube Como Despejar Z En Numeros Complejos Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. Despejando la incógnita z obtenemos que: En este capítulo mostraremos los números complejos, e introduciremos los principales. Los números complejos pueden sumarse coordenada a coordenada. En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas. Como Despejar Z En Numeros Complejos.
From corazondelapuna.blogspot.com
Despeje De Ecuaciones Calculadora Balan Como Despejar Z En Numeros Complejos Si z=a+bi y w=c+di z+w = (a+bi) + (c+di) = (a+c)+(b+d)i. En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. En este capítulo mostraremos los números complejos, e introduciremos los principales. Sabemos que la tangente no está definida en 90 o y 270. Como Despejar Z En Numeros Complejos.
From matematicassfaciless.blogspot.com
Matemáticas Fáciles Clasificación de los Números Complejos Como Despejar Z En Numeros Complejos Sabemos que la tangente no está definida en 90 o y 270 o. Despejando la incógnita z obtenemos que: En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. Si z=a+bi y w=c+di z+w = (a+bi) + (c+di) = (a+c)+(b+d)i. En este capítulo mostraremos. Como Despejar Z En Numeros Complejos.
From exoblnpjq.blob.core.windows.net
Como Despejar Y En Una Ecuacion De Primer Grado at Karen Nakamura blog Como Despejar Z En Numeros Complejos Despejando la incógnita z obtenemos que: En primer lugar pasamos el número complejo a forma polar: Como el afijo de z es. En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. Los números complejos pueden sumarse coordenada a coordenada. Los números complejos se. Como Despejar Z En Numeros Complejos.
From www.youtube.com
Números complejos. Operaciones con números complejos. Análisis complejo Como Despejar Z En Numeros Complejos En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas con números complejos, así como su aplicación en sistemas de ecuaciones y en geometría. Despejando la incógnita z obtenemos que: Los números complejos pueden sumarse coordenada a coordenada. Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz. Como Despejar Z En Numeros Complejos.
From resuelvetusdudas.es
Conjugado de un número complejo qué es y la fórmula de cómo calcularlo Como Despejar Z En Numeros Complejos En este capítulo mostraremos los números complejos, e introduciremos los principales. Los números complejos pueden sumarse coordenada a coordenada. Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. Despejando la incógnita z obtenemos que: En este artículo, exploraremos la resolución de ecuaciones lineales, cuadráticas y cúbicas. Como Despejar Z En Numeros Complejos.
From www.youtube.com
4. Ecuaciones sencillas, cómo despejar a x en el orden correcto. YouTube Como Despejar Z En Numeros Complejos Los números complejos se basan en la idea de poder definir el número i (llamado unidad imaginaria) como la raíz cuadrada principal de. En este capítulo mostraremos los números complejos, e introduciremos los principales. Despejando la incógnita z obtenemos que: Los números complejos pueden sumarse coordenada a coordenada. Si z=a+bi y w=c+di z+w = (a+bi) + (c+di) = (a+c)+(b+d)i. En. Como Despejar Z En Numeros Complejos.
From calculo.cc
Ejercicios resueltos de ecuaciones y sistemas con números complejos. Como Despejar Z En Numeros Complejos En este capítulo mostraremos los números complejos, e introduciremos los principales. En primer lugar pasamos el número complejo a forma polar: Sabemos que la tangente no está definida en 90 o y 270 o. Los números complejos pueden sumarse coordenada a coordenada. Si z=a+bi y w=c+di z+w = (a+bi) + (c+di) = (a+c)+(b+d)i. Despejando la incógnita z obtenemos que: En. Como Despejar Z En Numeros Complejos.