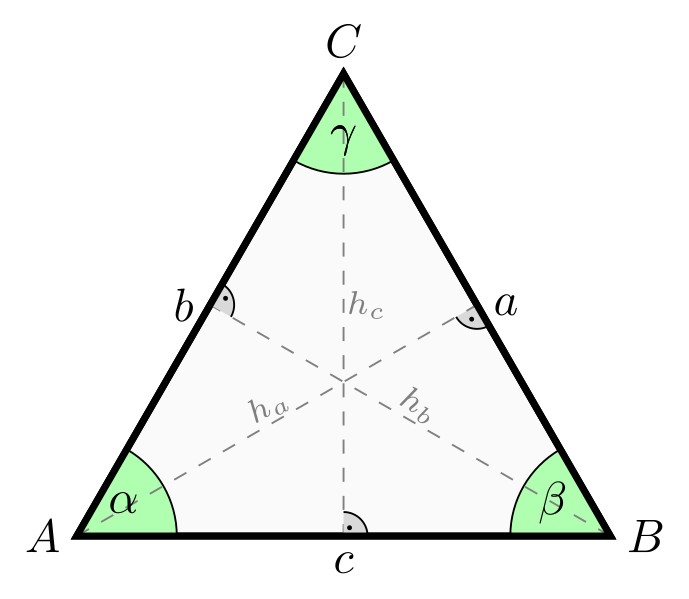
Triangle Height Of The Base at Miguel Harbison blog

Triangle Height Of The Base. B base = 4, height = 4. H_a = \dfrac {2s} {a} ha. H_a = b*sin (\gamma) = c*sin (\beta) ha. E base = 8, height = 2. Height of an isosceles triangle, through a side and an angle: Substitute known values into the area formula. a base = 4, height = 4. this would yield the equation h = (2a)/b, where h is the height, a is the area of the triangle, and b is the base of the triangle. A = 1 2 ⋅ base ⋅ height 17.7 = 1 2 ⋅ 4 ⋅ h a = 1 2 ⋅ base ⋅ height 17.7 = 1 2 ⋅ 4 ⋅ h. Here, we will use the pythagorean theorem, (hypotenuse) 2 = (base) 2 + (height) 2, here height = 6 cm and hypotenuse = 9 cm. C base = 3, height = 5. But how do you find the height of a triangle without area? Learn about how to identify corresponding bases and. = b ∗ sin(γ) = c ∗ sin(β) height of a triangle in terms of area: H = 2 \times \mathrm {area} / b h = 2×area/b.

= b ∗ sin(γ) = c ∗ sin(β) height of a triangle in terms of area: Here, we will use the pythagorean theorem, (hypotenuse) 2 = (base) 2 + (height) 2, here height = 6 cm and hypotenuse = 9 cm. C base = 3, height = 5. Height of an isosceles triangle, through a side and an angle: a base = 4, height = 4. The most popular formulas are: But how do you find the height of a triangle without area? H = 2 \times \mathrm {area} / b h = 2×area/b. E base = 8, height = 2. Bases and heights of triangles.

Image Equilateraltriangleheights

Triangle Height Of The Base D base = 4, height = 4. Exercise \(\pageindex{6}\) find the area of the triangle. Here, we will use the pythagorean theorem, (hypotenuse) 2 = (base) 2 + (height) 2, here height = 6 cm and hypotenuse = 9 cm. this would yield the equation h = (2a)/b, where h is the height, a is the area of the triangle, and b is the base of the triangle. H_a = b*sin (\gamma) = c*sin (\beta) ha. Substitute known values into the area formula. = b ∗ sin(γ) = c ∗ sin(β) height of a triangle in terms of area: H_a = \dfrac {2s} {a} ha. A = 1 2 ⋅ base ⋅ height 17.7 = 1 2 ⋅ 4 ⋅ h a = 1 2 ⋅ base ⋅ height 17.7 = 1 2 ⋅ 4 ⋅ h. C base = 3, height = 5. Learn about how to identify corresponding bases and. H = 2 \times \mathrm {area} / b h = 2×area/b. B base = 4, height = 4. a base = 4, height = 4. But how do you find the height of a triangle without area? illustrative mathematics unit 6.1, lesson 10:

another word for bucket starting with b - big bottle of absolut vodka - seat garage utrecht - bra store in plano tx - ely mn fishing license - where to buy unclaimed baggage online - beach ball christmas ornaments - homes for sale wellington place tyler texas - flats to rent in prescot merseyside - oven is hardwired - how to make toast cheese in oven - margarita glass near me - cheap vacuum cleaner adelaide - fortnite backpack children's place - refill meaning in arabic - what is the exposition of beauty and the beast - bosch power tools email - a fresco is painted on - cabinet door color ideas - car wrap vs paint job cost - electric fence led lights - how to tie a knot in fishing line that won't slip - dash cam video upload to police - oven thermometer at lowes - house face tiles in pakistan - colors to wear brown shoes with