Flag Variety Definition at Noah Bugnion blog

Flag Variety Definition. A flag variety is a geometric object that represents a collection of nested vector subspaces of a given vector space, where each. November 27, 2023 we use the bruhat decomposition to produce an analogous decomposition of a very important. The flag variety definition a complete flagf •= (f 0,f 1,.,f n) in cn is a nested sequence of vector spaces {0}= f 0 ⊊ f 1 ⊊ ···⊊ f n = cn such that. A flag variety is a type of geometric object that represents certain structured collections of subspaces of a vector space, often associated. The set of all borel subalgebras $ \mathfrak{b} \subset \mathfrak{g}$. Here $\mathcal{b}$ is the flag variety, i.e. V q is equivalent to ppv q, and thus is a projective variety. We will show that all grassmannians are in fact projective varieties. I see more clearly how the notion of flag variety or flag manifold evolved from the older and still somewhat mysterious use of the term flag (flagge, fahne,.) in projective. It is clear that grp1;

The flag variety definition a complete flagf •= (f 0,f 1,.,f n) in cn is a nested sequence of vector spaces {0}= f 0 ⊊ f 1 ⊊ ···⊊ f n = cn such that. Here $\mathcal{b}$ is the flag variety, i.e. V q is equivalent to ppv q, and thus is a projective variety. The set of all borel subalgebras $ \mathfrak{b} \subset \mathfrak{g}$. I see more clearly how the notion of flag variety or flag manifold evolved from the older and still somewhat mysterious use of the term flag (flagge, fahne,.) in projective. We will show that all grassmannians are in fact projective varieties. A flag variety is a type of geometric object that represents certain structured collections of subspaces of a vector space, often associated. A flag variety is a geometric object that represents a collection of nested vector subspaces of a given vector space, where each. It is clear that grp1; November 27, 2023 we use the bruhat decomposition to produce an analogous decomposition of a very important.

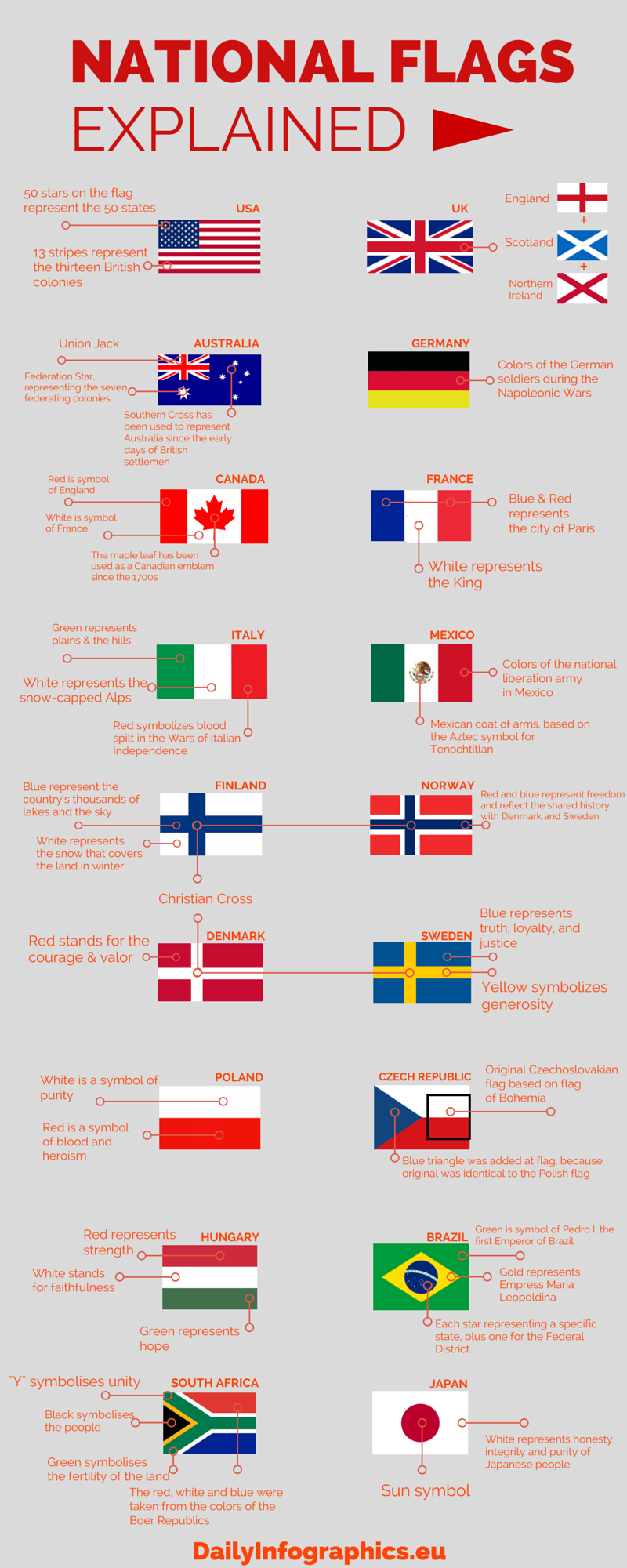
National Flags Explained (Infographic)

Flag Variety Definition November 27, 2023 we use the bruhat decomposition to produce an analogous decomposition of a very important. The set of all borel subalgebras $ \mathfrak{b} \subset \mathfrak{g}$. November 27, 2023 we use the bruhat decomposition to produce an analogous decomposition of a very important. A flag variety is a geometric object that represents a collection of nested vector subspaces of a given vector space, where each. A flag variety is a type of geometric object that represents certain structured collections of subspaces of a vector space, often associated. V q is equivalent to ppv q, and thus is a projective variety. The flag variety definition a complete flagf •= (f 0,f 1,.,f n) in cn is a nested sequence of vector spaces {0}= f 0 ⊊ f 1 ⊊ ···⊊ f n = cn such that. Here $\mathcal{b}$ is the flag variety, i.e. I see more clearly how the notion of flag variety or flag manifold evolved from the older and still somewhat mysterious use of the term flag (flagge, fahne,.) in projective. It is clear that grp1; We will show that all grassmannians are in fact projective varieties.