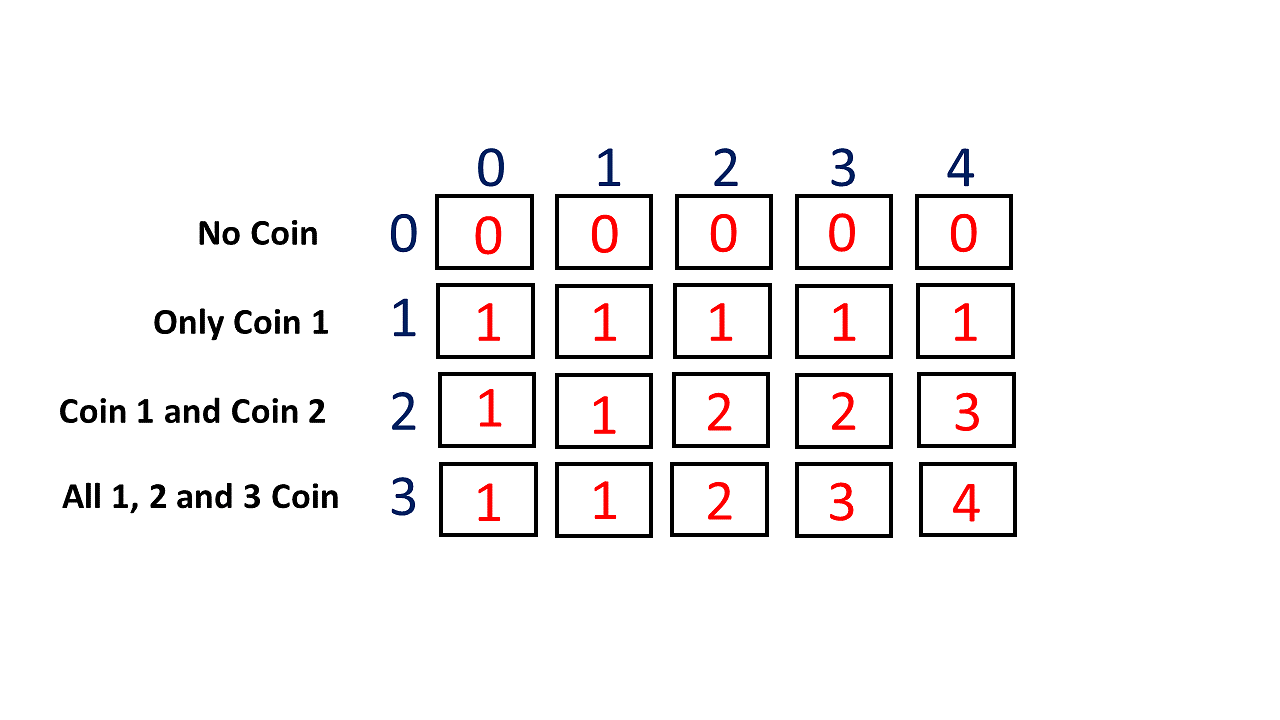
Coin Change Problem Optimal Substructure . One of the problems most commonly used to explain dynamic programming is the coin change. A given problem is said to have optimal substructure property if the optimal solution of the given problem can be obtained. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. Consider any optimal solution to making change for n. To minimize 1 + k, we must choose k as small as possible. The above recursive solution has optimal substructure and overlapping subproblems so dynamic programming (memoization) can be used to solve the problem.
from www.simplilearn.com
The above recursive solution has optimal substructure and overlapping subproblems so dynamic programming (memoization) can be used to solve the problem. Consider any optimal solution to making change for n. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. One of the problems most commonly used to explain dynamic programming is the coin change. A given problem is said to have optimal substructure property if the optimal solution of the given problem can be obtained. To minimize 1 + k, we must choose k as small as possible.
Coin Change Problem with Dynamic Programming A Complete Guide Simplilearn
Coin Change Problem Optimal Substructure A given problem is said to have optimal substructure property if the optimal solution of the given problem can be obtained. The above recursive solution has optimal substructure and overlapping subproblems so dynamic programming (memoization) can be used to solve the problem. Consider any optimal solution to making change for n. A given problem is said to have optimal substructure property if the optimal solution of the given problem can be obtained. One of the problems most commonly used to explain dynamic programming is the coin change. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. To minimize 1 + k, we must choose k as small as possible.
From www.slideserve.com
PPT Design and Analysis of Algorithms Greedy algorithms, coin changing problem PowerPoint Coin Change Problem Optimal Substructure Consider any optimal solution to making change for n. To minimize 1 + k, we must choose k as small as possible. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. The above recursive solution has optimal substructure and overlapping subproblems. Coin Change Problem Optimal Substructure.
From www.bitcoininsider.org
The Coin Change Problem — Explained Bitcoin Insider Coin Change Problem Optimal Substructure To minimize 1 + k, we must choose k as small as possible. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. Consider any optimal solution to making change for n. The above recursive solution has optimal substructure and overlapping subproblems. Coin Change Problem Optimal Substructure.
From pencilprogrammer.com
Coin Change Problem using Dynamic Programming Pencil Programmer Coin Change Problem Optimal Substructure The above recursive solution has optimal substructure and overlapping subproblems so dynamic programming (memoization) can be used to solve the problem. To minimize 1 + k, we must choose k as small as possible. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the. Coin Change Problem Optimal Substructure.
From asyncq.com
How to Solve Coin Change Problem Async Queue Coin Change Problem Optimal Substructure The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. A given problem is said to have optimal substructure property if the optimal solution of the given problem can be obtained. One of the problems most commonly used to explain dynamic programming. Coin Change Problem Optimal Substructure.
From es.scribd.com
Coin Change Problem PDF Computer Science Areas Of Computer Science Coin Change Problem Optimal Substructure Consider any optimal solution to making change for n. One of the problems most commonly used to explain dynamic programming is the coin change. To minimize 1 + k, we must choose k as small as possible. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved. Coin Change Problem Optimal Substructure.
From www.bitcoininsider.org
The Coin Change Problem — Explained Bitcoin Insider Coin Change Problem Optimal Substructure One of the problems most commonly used to explain dynamic programming is the coin change. To minimize 1 + k, we must choose k as small as possible. Consider any optimal solution to making change for n. The above recursive solution has optimal substructure and overlapping subproblems so dynamic programming (memoization) can be used to solve the problem. The coin. Coin Change Problem Optimal Substructure.
From www.slideshare.net
Coin Change Problem Coin Change Problem Optimal Substructure To minimize 1 + k, we must choose k as small as possible. Consider any optimal solution to making change for n. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. The above recursive solution has optimal substructure and overlapping subproblems. Coin Change Problem Optimal Substructure.
From www.simplilearn.com
Coin Change Problem with Dynamic Programming A Complete Guide Simplilearn Coin Change Problem Optimal Substructure The above recursive solution has optimal substructure and overlapping subproblems so dynamic programming (memoization) can be used to solve the problem. A given problem is said to have optimal substructure property if the optimal solution of the given problem can be obtained. To minimize 1 + k, we must choose k as small as possible. The coin changing problem has. Coin Change Problem Optimal Substructure.
From www.bitcoininsider.org
The Coin Change Problem — Explained Bitcoin Insider Coin Change Problem Optimal Substructure To minimize 1 + k, we must choose k as small as possible. A given problem is said to have optimal substructure property if the optimal solution of the given problem can be obtained. Consider any optimal solution to making change for n. The above recursive solution has optimal substructure and overlapping subproblems so dynamic programming (memoization) can be used. Coin Change Problem Optimal Substructure.
From www.docsity.com
The Coin Changing problem The Coin Changing problem Study Guides, Projects, Research Computer Coin Change Problem Optimal Substructure A given problem is said to have optimal substructure property if the optimal solution of the given problem can be obtained. Consider any optimal solution to making change for n. To minimize 1 + k, we must choose k as small as possible. One of the problems most commonly used to explain dynamic programming is the coin change. The coin. Coin Change Problem Optimal Substructure.
From dokumen.tips
(PDF) Coin Change problem using DP DOKUMEN.TIPS Coin Change Problem Optimal Substructure Consider any optimal solution to making change for n. The above recursive solution has optimal substructure and overlapping subproblems so dynamic programming (memoization) can be used to solve the problem. A given problem is said to have optimal substructure property if the optimal solution of the given problem can be obtained. One of the problems most commonly used to explain. Coin Change Problem Optimal Substructure.
From www.codespeedy.com
Coin Change Problem in C++ CodeSpeedy Coin Change Problem Optimal Substructure One of the problems most commonly used to explain dynamic programming is the coin change. A given problem is said to have optimal substructure property if the optimal solution of the given problem can be obtained. The above recursive solution has optimal substructure and overlapping subproblems so dynamic programming (memoization) can be used to solve the problem. To minimize 1. Coin Change Problem Optimal Substructure.
From progressivecoder.com
Coin Change Problem using Greedy Algorithm PROGRESSIVE CODER Coin Change Problem Optimal Substructure Consider any optimal solution to making change for n. The above recursive solution has optimal substructure and overlapping subproblems so dynamic programming (memoization) can be used to solve the problem. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. To minimize. Coin Change Problem Optimal Substructure.
From www.chegg.com
Solved Consider solving the Coin Change problem on the Coin Change Problem Optimal Substructure A given problem is said to have optimal substructure property if the optimal solution of the given problem can be obtained. To minimize 1 + k, we must choose k as small as possible. One of the problems most commonly used to explain dynamic programming is the coin change. The above recursive solution has optimal substructure and overlapping subproblems so. Coin Change Problem Optimal Substructure.
From www.studocu.com
Coin Change Problem watermark Coin Change Problem Problem Given a set of coins and a value V Coin Change Problem Optimal Substructure A given problem is said to have optimal substructure property if the optimal solution of the given problem can be obtained. One of the problems most commonly used to explain dynamic programming is the coin change. To minimize 1 + k, we must choose k as small as possible. The above recursive solution has optimal substructure and overlapping subproblems so. Coin Change Problem Optimal Substructure.
From www.youtube.com
[Algorithms] Optimalsubstructure property of the longest common subsequence problem YouTube Coin Change Problem Optimal Substructure Consider any optimal solution to making change for n. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. One of the problems most commonly used to explain dynamic programming is the coin change. A given problem is said to have optimal. Coin Change Problem Optimal Substructure.
From strncat.github.io
Method 3 Dynamic Programming Coin Change Problem Optimal Substructure Consider any optimal solution to making change for n. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. To minimize 1 + k, we must choose k as small as possible. The above recursive solution has optimal substructure and overlapping subproblems. Coin Change Problem Optimal Substructure.
From favtutor.com
Minimum Coin Change Problem & 2 Solutions (Recursion & DP) Coin Change Problem Optimal Substructure The above recursive solution has optimal substructure and overlapping subproblems so dynamic programming (memoization) can be used to solve the problem. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. Consider any optimal solution to making change for n. To minimize. Coin Change Problem Optimal Substructure.
From www.chegg.com
Solved 2. Read the Coin Changing Problem in the handout on Coin Change Problem Optimal Substructure Consider any optimal solution to making change for n. One of the problems most commonly used to explain dynamic programming is the coin change. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. A given problem is said to have optimal. Coin Change Problem Optimal Substructure.
From hackernoon.com
The Coin Change Problem — Explained HackerNoon Coin Change Problem Optimal Substructure One of the problems most commonly used to explain dynamic programming is the coin change. To minimize 1 + k, we must choose k as small as possible. Consider any optimal solution to making change for n. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved. Coin Change Problem Optimal Substructure.
From slideplayer.com
10/31/02CSE Greedy Algorithms CSE Algorithms Greedy Algorithms. ppt download Coin Change Problem Optimal Substructure To minimize 1 + k, we must choose k as small as possible. Consider any optimal solution to making change for n. The above recursive solution has optimal substructure and overlapping subproblems so dynamic programming (memoization) can be used to solve the problem. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler. Coin Change Problem Optimal Substructure.
From www.slideserve.com
PPT Design and Analysis of Algorithms Greedy algorithms, coin changing problem PowerPoint Coin Change Problem Optimal Substructure The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. One of the problems most commonly used to explain dynamic programming is the coin change. To minimize 1 + k, we must choose k as small as possible. Consider any optimal solution. Coin Change Problem Optimal Substructure.
From www.bitcoininsider.org
The Coin Change Problem — Explained Bitcoin Insider Coin Change Problem Optimal Substructure The above recursive solution has optimal substructure and overlapping subproblems so dynamic programming (memoization) can be used to solve the problem. A given problem is said to have optimal substructure property if the optimal solution of the given problem can be obtained. One of the problems most commonly used to explain dynamic programming is the coin change. To minimize 1. Coin Change Problem Optimal Substructure.
From www.youtube.com
Coin Change Problem Problem Statement Example with Explanation YouTube Coin Change Problem Optimal Substructure To minimize 1 + k, we must choose k as small as possible. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. A given problem is said to have optimal substructure property if the optimal solution of the given problem can. Coin Change Problem Optimal Substructure.
From slideplayer.com
Design and Analysis of Algorithms ppt download Coin Change Problem Optimal Substructure The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. To minimize 1 + k, we must choose k as small as possible. One of the problems most commonly used to explain dynamic programming is the coin change. The above recursive solution. Coin Change Problem Optimal Substructure.
From www.slideserve.com
PPT Design and Analysis of Algorithms Greedy algorithms, coin changing problem PowerPoint Coin Change Problem Optimal Substructure A given problem is said to have optimal substructure property if the optimal solution of the given problem can be obtained. Consider any optimal solution to making change for n. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. One of. Coin Change Problem Optimal Substructure.
From www.slideserve.com
PPT Design and Analysis of Algorithms Greedy algorithms, coin changing problem PowerPoint Coin Change Problem Optimal Substructure Consider any optimal solution to making change for n. To minimize 1 + k, we must choose k as small as possible. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. A given problem is said to have optimal substructure property. Coin Change Problem Optimal Substructure.
From www.slideserve.com
PPT Design and Analysis of Algorithms Greedy algorithms, coin changing problem PowerPoint Coin Change Problem Optimal Substructure A given problem is said to have optimal substructure property if the optimal solution of the given problem can be obtained. The above recursive solution has optimal substructure and overlapping subproblems so dynamic programming (memoization) can be used to solve the problem. To minimize 1 + k, we must choose k as small as possible. Consider any optimal solution to. Coin Change Problem Optimal Substructure.
From www.interviewbit.com
Coin Change Problem InterviewBit Coin Change Problem Optimal Substructure One of the problems most commonly used to explain dynamic programming is the coin change. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. Consider any optimal solution to making change for n. To minimize 1 + k, we must choose. Coin Change Problem Optimal Substructure.
From www.simplilearn.com
Coin Change Problem with Dynamic Programming A Complete Guide Simplilearn Coin Change Problem Optimal Substructure The above recursive solution has optimal substructure and overlapping subproblems so dynamic programming (memoization) can be used to solve the problem. A given problem is said to have optimal substructure property if the optimal solution of the given problem can be obtained. One of the problems most commonly used to explain dynamic programming is the coin change. Consider any optimal. Coin Change Problem Optimal Substructure.
From www.youtube.com
Greedy Algorithm and Coin Changing Problem CSE2117 Spring21 YouTube Coin Change Problem Optimal Substructure The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. To minimize 1 + k, we must choose k as small as possible. The above recursive solution has optimal substructure and overlapping subproblems so dynamic programming (memoization) can be used to solve. Coin Change Problem Optimal Substructure.
From www.youtube.com
Christo Ananth Dynamic programming, Principle of optimality, Coin Changing Problem Coin Change Problem Optimal Substructure To minimize 1 + k, we must choose k as small as possible. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. One of the problems most commonly used to explain dynamic programming is the coin change. The above recursive solution. Coin Change Problem Optimal Substructure.
From www.simplilearn.com.cach3.com
Coin Change Problem with Dynamic Programming A Complete Guide Simplilearn Coin Change Problem Optimal Substructure One of the problems most commonly used to explain dynamic programming is the coin change. Consider any optimal solution to making change for n. A given problem is said to have optimal substructure property if the optimal solution of the given problem can be obtained. The above recursive solution has optimal substructure and overlapping subproblems so dynamic programming (memoization) can. Coin Change Problem Optimal Substructure.
From www.chegg.com
Solved Consider the coin change problem defined as follows. Coin Change Problem Optimal Substructure A given problem is said to have optimal substructure property if the optimal solution of the given problem can be obtained. One of the problems most commonly used to explain dynamic programming is the coin change. The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to. Coin Change Problem Optimal Substructure.
From www.youtube.com
Minimum coin change problem Dynamic programming Python Minimum coin change leetcode YouTube Coin Change Problem Optimal Substructure The coin changing problem has both optimal substructure, meaning that it can be easily divided to simpler problems and they can be solved to find the final solution. One of the problems most commonly used to explain dynamic programming is the coin change. A given problem is said to have optimal substructure property if the optimal solution of the given. Coin Change Problem Optimal Substructure.