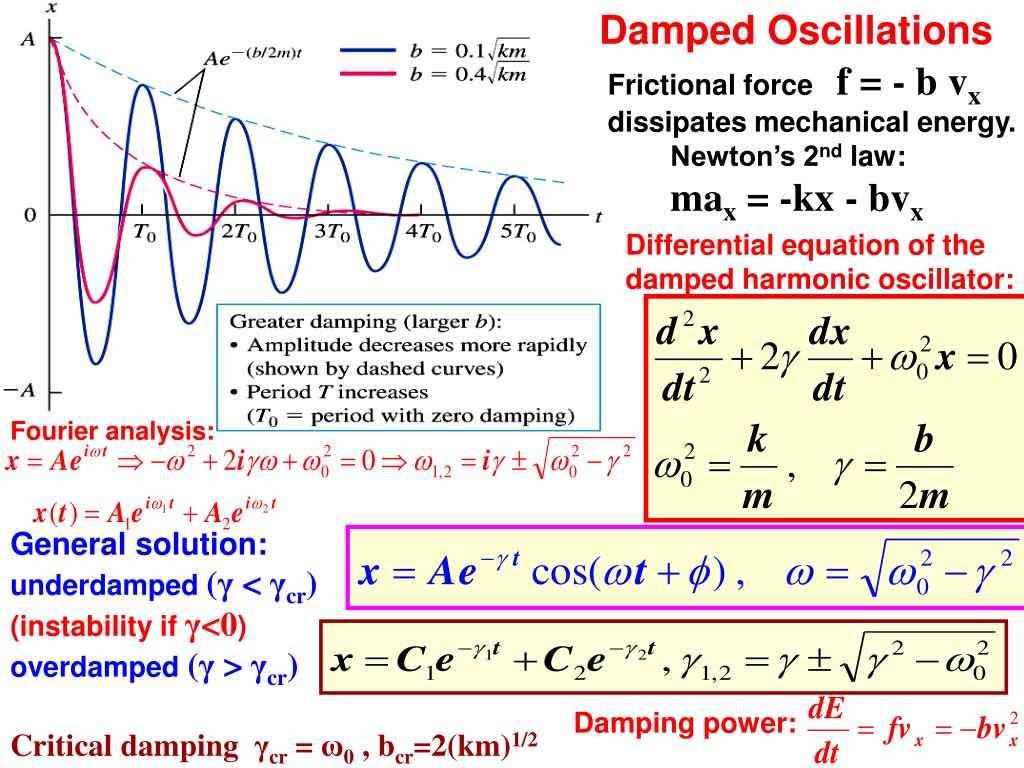
Differential Equation Of Forced Harmonic Oscillator at Adolfo Scanlan blog

Differential Equation Of Forced Harmonic Oscillator. Explain the concept of resonance and its impact on the amplitude of an oscillator. Use this geogebra applet 3 to explore the behaviour of a forced damped harmonic oscillator. My00 + by0 + ky = f. X0(ω) = f0 / m ((b / m)2ω2 + (ω2 0 − ω2)2)1 / 2. Try to find the practical resonance for some choice of parameters. Our differential equation can now be written as \[f_{0} e^{i \omega t}=m \frac{d^{2} z}{d t^{2}}+b \frac{d z}{d t}+k z \nonumber \] we. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ Solution to the forced damped oscillator equation. In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force f. In this section, we briefly explore applying a periodic driving force acting on a simple harmonic oscillator. List the characteristics of a system oscillating in resonance. List the equations of motion associated with forced oscillations. How to solve harmonic oscillator differential equation: We derive the solution to equation (23.6.4) in appendix 23e: The driving force puts energy into the.

The solution to is given by the function. List the equations of motion associated with forced oscillations. In this section, we briefly explore applying a periodic driving force acting on a simple harmonic oscillator. In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force f. X(t) = x0cos(ωt + ϕ) where the amplitude x0 is a function of the driving angular frequency ω and is given by. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ Explain the concept of resonance and its impact on the amplitude of an oscillator. We derive the solution to equation (23.6.4) in appendix 23e: X0(ω) = f0 / m ((b / m)2ω2 + (ω2 0 − ω2)2)1 / 2. List the characteristics of a system oscillating in resonance.

PPT Periodic Motion and Theory of Oscillations PowerPoint Presentation ID1017807

Differential Equation Of Forced Harmonic Oscillator $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ List the equations of motion associated with forced oscillations. Use this geogebra applet 3 to explore the behaviour of a forced damped harmonic oscillator. Try to find the practical resonance for some choice of parameters. The driving force puts energy into the. We derive the solution to equation (23.6.4) in appendix 23e: Explain the concept of resonance and its impact on the amplitude of an oscillator. List the characteristics of a system oscillating in resonance. X(t) = x0cos(ωt + ϕ) where the amplitude x0 is a function of the driving angular frequency ω and is given by. $\dfrac{d^2x}{dt^2} + \dfrac{kx}{m} = 0$ My00 + by0 + ky = f. The solution to is given by the function. In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force f. Our differential equation can now be written as \[f_{0} e^{i \omega t}=m \frac{d^{2} z}{d t^{2}}+b \frac{d z}{d t}+k z \nonumber \] we. X0(ω) = f0 / m ((b / m)2ω2 + (ω2 0 − ω2)2)1 / 2. In this section, we briefly explore applying a periodic driving force acting on a simple harmonic oscillator.