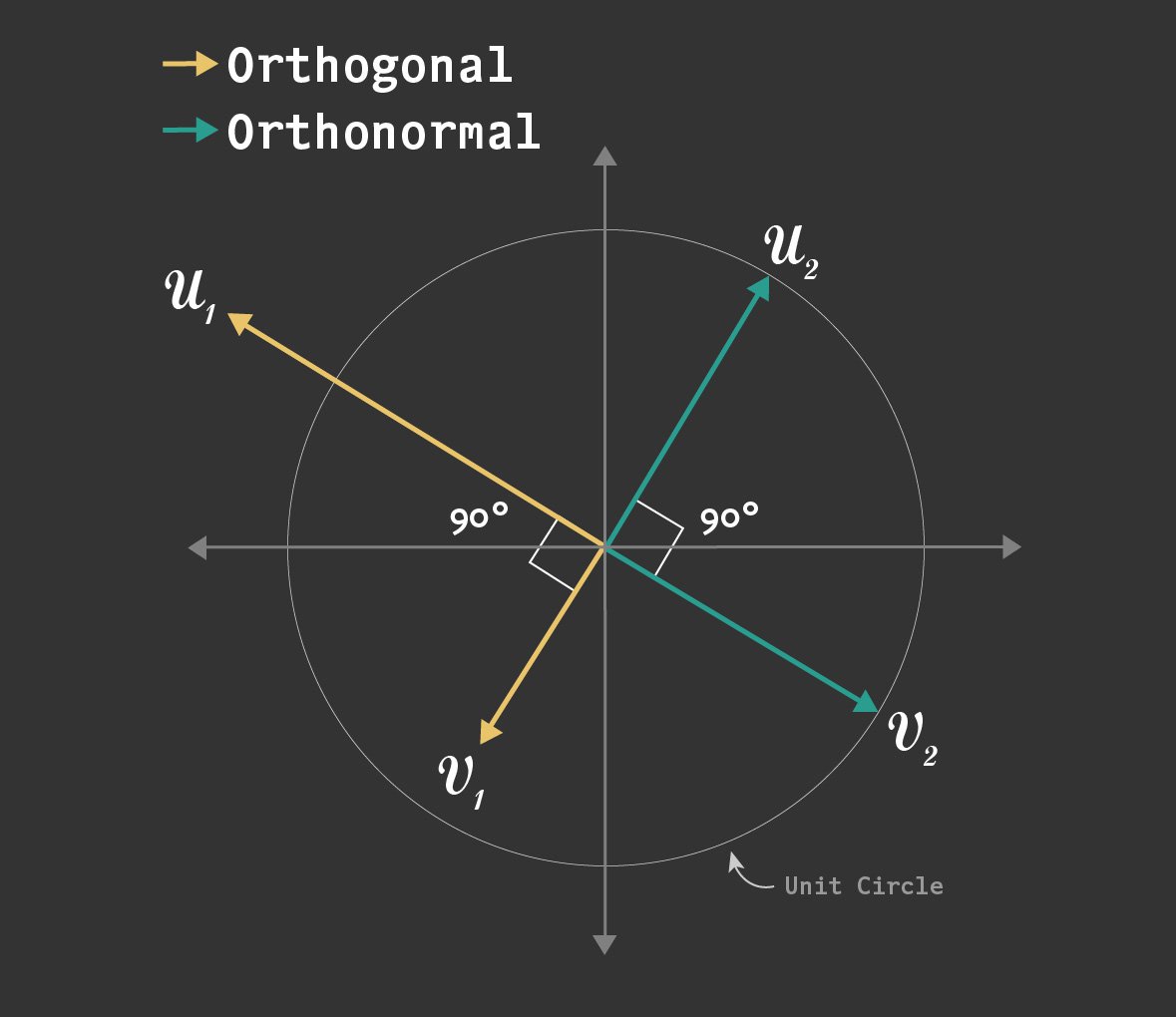
Meaning Of Orthogonal Matrix . By the end of this blog post, you’ll. Learn more about the orthogonal matrices along with. Orthogonal matrices are defined by two key concepts in linear algebra: When the product of one matrix with its transpose matrix gives the identity matrix value, then that matrix is termed orthogonal matrix. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Also, the product of an orthogonal matrix and its transpose is equal to i. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every. These matrices are useful in science for many vector related. The transpose of a matrix and the inverse of a matrix. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix.
from www.learndatasci.com
Learn more about the orthogonal matrices along with. The transpose of a matrix and the inverse of a matrix. Orthogonal matrices are defined by two key concepts in linear algebra: Also, the product of an orthogonal matrix and its transpose is equal to i. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. By the end of this blog post, you’ll. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every. When the product of one matrix with its transpose matrix gives the identity matrix value, then that matrix is termed orthogonal matrix. These matrices are useful in science for many vector related. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix.
Orthogonal and Orthonormal Vectors LearnDataSci
Meaning Of Orthogonal Matrix Learn more about the orthogonal matrices along with. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Also, the product of an orthogonal matrix and its transpose is equal to i. These matrices are useful in science for many vector related. By the end of this blog post, you’ll. When the product of one matrix with its transpose matrix gives the identity matrix value, then that matrix is termed orthogonal matrix. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Learn more about the orthogonal matrices along with. Orthogonal matrices are defined by two key concepts in linear algebra: The transpose of a matrix and the inverse of a matrix.
From www.youtube.com
Orthogonal and Orthonormal Vectors Linear Algebra YouTube Meaning Of Orthogonal Matrix Also, the product of an orthogonal matrix and its transpose is equal to i. The transpose of a matrix and the inverse of a matrix. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every. By the end of this. Meaning Of Orthogonal Matrix.
From scoop.eduncle.com
What do you mean by two rows or columnsof unitary matrix are orthogonal Meaning Of Orthogonal Matrix These matrices are useful in science for many vector related. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Also, the product of an orthogonal matrix and its transpose is equal to i. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each. Meaning Of Orthogonal Matrix.
From www.learndatasci.com
Orthogonal and Orthonormal Vectors LearnDataSci Meaning Of Orthogonal Matrix Learn more about the orthogonal matrices along with. These matrices are useful in science for many vector related. When the product of one matrix with its transpose matrix gives the identity matrix value, then that matrix is termed orthogonal matrix. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each. Meaning Of Orthogonal Matrix.
From www.chegg.com
Solved An orthogonal matrix is one for which its transpose Meaning Of Orthogonal Matrix Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every. When the product of one matrix with its transpose matrix gives the identity matrix value, then that matrix is termed orthogonal matrix. A matrix 'a' is orthogonal if and only. Meaning Of Orthogonal Matrix.
From www.youtube.com
10]Orthogonal Matrix with It's Definition, Properties & Example Meaning Of Orthogonal Matrix The transpose of a matrix and the inverse of a matrix. These matrices are useful in science for many vector related. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every. Learn more about the orthogonal matrices along with. Also,. Meaning Of Orthogonal Matrix.
From klazemyrp.blob.core.windows.net
How To Tell If A Matrix Is Orthogonal at Nancy Rameriz blog Meaning Of Orthogonal Matrix A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Also, the product of an orthogonal matrix and its transpose is equal to i. Learn more about the orthogonal matrices along with. These matrices are useful in science for many vector related. Orthogonal matrix is a. Meaning Of Orthogonal Matrix.
From www.youtube.com
What is Orthogonal Matrix and its Properties Kamaldheeriya YouTube Meaning Of Orthogonal Matrix When the product of one matrix with its transpose matrix gives the identity matrix value, then that matrix is termed orthogonal matrix. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every. The transpose of a matrix and the inverse. Meaning Of Orthogonal Matrix.
From klazemyrp.blob.core.windows.net
How To Tell If A Matrix Is Orthogonal at Nancy Rameriz blog Meaning Of Orthogonal Matrix Orthogonal matrices are defined by two key concepts in linear algebra: Also, the product of an orthogonal matrix and its transpose is equal to i. When the product of one matrix with its transpose matrix gives the identity matrix value, then that matrix is termed orthogonal matrix. By the end of this blog post, you’ll. The transpose of a matrix. Meaning Of Orthogonal Matrix.
From www.youtube.com
Trick to find Inverse of (A.A^T) of Orthogonal Matrix GATE question Meaning Of Orthogonal Matrix The transpose of a matrix and the inverse of a matrix. Learn more about the orthogonal matrices along with. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the. Meaning Of Orthogonal Matrix.
From ssaru.github.io
(MML Book 선형대수 Chapter 3.4) Angles and Orthogonality Martin Hwang Meaning Of Orthogonal Matrix Learn more about the orthogonal matrices along with. The transpose of a matrix and the inverse of a matrix. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors,. Meaning Of Orthogonal Matrix.
From slidetodoc.com
Orthogonal Vector Hungyi Lee Orthogonal Set A set Meaning Of Orthogonal Matrix Also, the product of an orthogonal matrix and its transpose is equal to i. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every. The transpose of a matrix and the inverse of a matrix. Learn more about the orthogonal. Meaning Of Orthogonal Matrix.
From datascienceparichay.com
Numpy Check If a Matrix is Orthogonal Data Science Parichay Meaning Of Orthogonal Matrix These matrices are useful in science for many vector related. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every. By the end of this blog post, you’ll. Learn more about the orthogonal matrices along with. Also, the product of. Meaning Of Orthogonal Matrix.
From limfadreams.weebly.com
Orthogonal matrix limfadreams Meaning Of Orthogonal Matrix A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every. These matrices are useful in science for many vector related. A n×n matrix a. Meaning Of Orthogonal Matrix.
From www.slideshare.net
Orthogonal porjection in statistics Meaning Of Orthogonal Matrix A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. When the product of one matrix with its transpose matrix gives the identity matrix value, then that matrix is termed orthogonal matrix. By the end of this blog post, you’ll. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is. Meaning Of Orthogonal Matrix.
From moriah-has-stanton.blogspot.com
When Is a Matrix Orthogonally Diagonalizable MoriahhasStanton Meaning Of Orthogonal Matrix Learn more about the orthogonal matrices along with. These matrices are useful in science for many vector related. The transpose of a matrix and the inverse of a matrix. Orthogonal matrices are defined by two key concepts in linear algebra: Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each. Meaning Of Orthogonal Matrix.
From youtube.com
1.3 Orthogonal Vectors YouTube Meaning Of Orthogonal Matrix Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every. Learn more about the orthogonal matrices along with. Orthogonal matrices are defined by two key concepts in linear algebra: A matrix 'a' is orthogonal if and only if its inverse. Meaning Of Orthogonal Matrix.
From www.slideserve.com
PPT 5.1 Orthogonality PowerPoint Presentation, free download ID2094487 Meaning Of Orthogonal Matrix A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. The transpose of a matrix and the inverse of a matrix. Also, the product of an orthogonal matrix and its. Meaning Of Orthogonal Matrix.
From scoop.eduncle.com
Find orthogonal matrix and unitary matrix Meaning Of Orthogonal Matrix Learn more about the orthogonal matrices along with. The transpose of a matrix and the inverse of a matrix. Orthogonal matrices are defined by two key concepts in linear algebra: Also, the product of an orthogonal matrix and its transpose is equal to i. When the product of one matrix with its transpose matrix gives the identity matrix value, then. Meaning Of Orthogonal Matrix.
From www.slideserve.com
PPT Elementary Linear Algebra Anton & Rorres, 9 th Edition PowerPoint Meaning Of Orthogonal Matrix Also, the product of an orthogonal matrix and its transpose is equal to i. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every. The transpose of a matrix and the inverse of a matrix. When the product of one. Meaning Of Orthogonal Matrix.
From www.slideserve.com
PPT ENGG2013 Unit 19 The principal axes theorem PowerPoint Meaning Of Orthogonal Matrix The transpose of a matrix and the inverse of a matrix. By the end of this blog post, you’ll. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Learn. Meaning Of Orthogonal Matrix.
From math.stackexchange.com
orthogonality How would I go about solving this projection matrices Meaning Of Orthogonal Matrix Also, the product of an orthogonal matrix and its transpose is equal to i. The transpose of a matrix and the inverse of a matrix. These matrices are useful in science for many vector related. Orthogonal matrices are defined by two key concepts in linear algebra: Learn more about the orthogonal matrices along with. A matrix 'a' is orthogonal if. Meaning Of Orthogonal Matrix.
From www.machinelearningplus.com
Linear Algebra Archives Machine Learning Plus Meaning Of Orthogonal Matrix A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. The transpose of a matrix and the inverse of a matrix. These matrices are useful in science for many vector. Meaning Of Orthogonal Matrix.
From www.youtube.com
An orthogonal set of vectors having a span that contains p, q, r is Meaning Of Orthogonal Matrix Orthogonal matrices are defined by two key concepts in linear algebra: Also, the product of an orthogonal matrix and its transpose is equal to i. The transpose of a matrix and the inverse of a matrix. Learn more about the orthogonal matrices along with. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose. Meaning Of Orthogonal Matrix.
From www.youtube.com
Orthogonal Matrix What is orthogonal Matrix How to prove Orthogonal Meaning Of Orthogonal Matrix By the end of this blog post, you’ll. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. When the product of one matrix with its transpose matrix gives the identity matrix value, then that matrix is termed orthogonal matrix. Orthogonal matrix is a square matrix in which all rows and columns are mutually. Meaning Of Orthogonal Matrix.
From klaxtukue.blob.core.windows.net
Orthogonal Matrix Theorems at Laura Yang blog Meaning Of Orthogonal Matrix The transpose of a matrix and the inverse of a matrix. When the product of one matrix with its transpose matrix gives the identity matrix value, then that matrix is termed orthogonal matrix. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. A matrix 'a'. Meaning Of Orthogonal Matrix.
From 911weknow.com
[Linear Algebra] 9. Properties of orthogonal matrices 911 WeKnow Meaning Of Orthogonal Matrix A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular to every. Also, the product of an orthogonal matrix and its transpose is equal to i.. Meaning Of Orthogonal Matrix.
From www.youtube.com
How to Prove that a Matrix is Orthogonal YouTube Meaning Of Orthogonal Matrix When the product of one matrix with its transpose matrix gives the identity matrix value, then that matrix is termed orthogonal matrix. Orthogonal matrices are defined by two key concepts in linear algebra: By the end of this blog post, you’ll. The transpose of a matrix and the inverse of a matrix. A n×n matrix a is an orthogonal matrix. Meaning Of Orthogonal Matrix.
From www.youtube.com
Orthogonal Matrix Definition Example Properties Class 12 Maths YouTube Meaning Of Orthogonal Matrix A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. These matrices are useful in science for many vector related. Learn more about the orthogonal matrices along with. Orthogonal matrix. Meaning Of Orthogonal Matrix.
From www.youtube.com
Orthogonal Matrix With Definition, Example and Properties YouTube Meaning Of Orthogonal Matrix Orthogonal matrices are defined by two key concepts in linear algebra: A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. When the product of one matrix with its transpose matrix gives the identity matrix value, then that matrix is termed orthogonal matrix. The transpose of. Meaning Of Orthogonal Matrix.
From www.youtube.com
Mathematics Symmetric, Skew Symmetric and Orthogonal Matrix YouTube Meaning Of Orthogonal Matrix These matrices are useful in science for many vector related. When the product of one matrix with its transpose matrix gives the identity matrix value, then that matrix is termed orthogonal matrix. By the end of this blog post, you’ll. Orthogonal matrices are defined by two key concepts in linear algebra: Orthogonal matrix is a square matrix in which all. Meaning Of Orthogonal Matrix.
From www.youtube.com
【Orthogonality】06 Orthogonal matrix YouTube Meaning Of Orthogonal Matrix These matrices are useful in science for many vector related. Orthogonal matrices are defined by two key concepts in linear algebra: When the product of one matrix with its transpose matrix gives the identity matrix value, then that matrix is termed orthogonal matrix. The transpose of a matrix and the inverse of a matrix. By the end of this blog. Meaning Of Orthogonal Matrix.
From slideplayer.com
Orthogonal Matrices & Symmetric Matrices ppt download Meaning Of Orthogonal Matrix When the product of one matrix with its transpose matrix gives the identity matrix value, then that matrix is termed orthogonal matrix. The transpose of a matrix and the inverse of a matrix. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. By the end of this blog post, you’ll. Orthogonal matrices are. Meaning Of Orthogonal Matrix.
From joidymkvo.blob.core.windows.net
Check If Matrix Is Orthogonal Matlab at Ann Vannote blog Meaning Of Orthogonal Matrix When the product of one matrix with its transpose matrix gives the identity matrix value, then that matrix is termed orthogonal matrix. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the. Meaning Of Orthogonal Matrix.
From www.youtube.com
Orthogonal Matrix example YouTube Meaning Of Orthogonal Matrix When the product of one matrix with its transpose matrix gives the identity matrix value, then that matrix is termed orthogonal matrix. Learn more about the orthogonal matrices along with. These matrices are useful in science for many vector related. A matrix 'a' is orthogonal if and only if its inverse is equal to its transpose. Also, the product of. Meaning Of Orthogonal Matrix.
From www.youtube.com
Properties of Orthogonal Matrix Example1 YouTube Meaning Of Orthogonal Matrix By the end of this blog post, you’ll. A n×n matrix a is an orthogonal matrix if aa^(t)=i, (1) where a^(t) is the transpose of a and i is the identity matrix. Orthogonal matrix is a square matrix in which all rows and columns are mutually orthogonal unit vectors, meaning that each row and column of the matrix is perpendicular. Meaning Of Orthogonal Matrix.