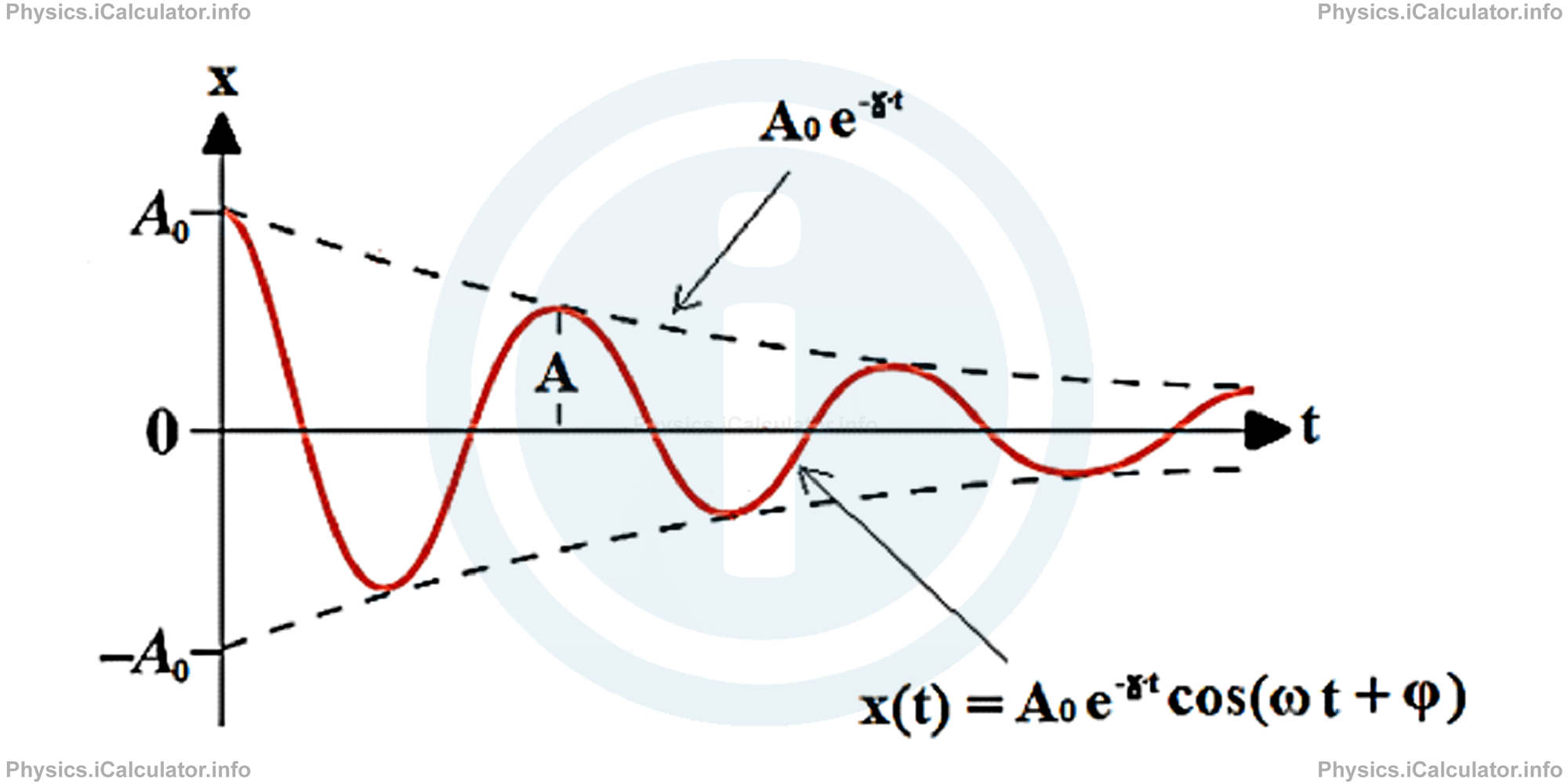
Damped Oscillator Kinetic Energy . — the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin. It is the sum of the kinetic energy ½mv 2 and the elastic potential. imagine some fraction of kinetic energy is couple to thermal energy per unit time β. — energy in the underdamped oscillator. the mechanical energy of any oscillator is proportional to the square of the amplitude. Where ∂l ∂q is the conservative force, and. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. For the underdamped oscillator, \((b / m)^{2}
from physics.icalculator.com
It is the sum of the kinetic energy ½mv 2 and the elastic potential. — the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin. the mechanical energy of any oscillator is proportional to the square of the amplitude. — energy in the underdamped oscillator. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. For the underdamped oscillator, \((b / m)^{2} Where ∂l ∂q is the conservative force, and. imagine some fraction of kinetic energy is couple to thermal energy per unit time β.
What is a RLC Circuit? Damped Oscillations in a RLC Circuit iCalcula
Damped Oscillator Kinetic Energy in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. — energy in the underdamped oscillator. — the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin. Where ∂l ∂q is the conservative force, and. For the underdamped oscillator, \((b / m)^{2} It is the sum of the kinetic energy ½mv 2 and the elastic potential. the mechanical energy of any oscillator is proportional to the square of the amplitude. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. imagine some fraction of kinetic energy is couple to thermal energy per unit time β.
From courses.physics.illinois.edu
Physics 111 Lab 8 Damped Oscillator Kinetic Energy — energy in the underdamped oscillator. imagine some fraction of kinetic energy is couple to thermal energy per unit time β. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. It is the sum of the kinetic energy ½mv 2 and the elastic potential. Where. Damped Oscillator Kinetic Energy.
From www.ehu.eus
Simple harmonic motion and damped oscillator Damped Oscillator Kinetic Energy — energy in the underdamped oscillator. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. For the underdamped oscillator, \((b / m)^{2} — the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin. the mechanical energy. Damped Oscillator Kinetic Energy.
From animalia-life.club
Damped Harmonic Oscillator Examples Damped Oscillator Kinetic Energy imagine some fraction of kinetic energy is couple to thermal energy per unit time β. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. the mechanical energy of any oscillator is proportional to the square of the amplitude. — energy in the underdamped oscillator.. Damped Oscillator Kinetic Energy.
From www.slideserve.com
PPT Damped Harmonic Motion PowerPoint Presentation, free download Damped Oscillator Kinetic Energy in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. — energy in the underdamped oscillator. Where ∂l ∂q is the conservative force, and. imagine some fraction of kinetic energy is couple to thermal energy per unit time β. For the underdamped oscillator, \((b / m)^{2}. Damped Oscillator Kinetic Energy.
From www.nagwa.com
Video Damped Oscillations Nagwa Damped Oscillator Kinetic Energy imagine some fraction of kinetic energy is couple to thermal energy per unit time β. It is the sum of the kinetic energy ½mv 2 and the elastic potential. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. For the underdamped oscillator, \((b / m)^{2} Where. Damped Oscillator Kinetic Energy.
From howwhy.nfshost.com
Damped Oscillation Damped Oscillator Kinetic Energy It is the sum of the kinetic energy ½mv 2 and the elastic potential. Where ∂l ∂q is the conservative force, and. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. the mechanical energy of any oscillator is proportional to the square of the amplitude. . Damped Oscillator Kinetic Energy.
From tikz.net
Harmonic oscillator plots Damped Oscillator Kinetic Energy — energy in the underdamped oscillator. the mechanical energy of any oscillator is proportional to the square of the amplitude. Where ∂l ∂q is the conservative force, and. For the underdamped oscillator, \((b / m)^{2} — the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin. in this. Damped Oscillator Kinetic Energy.
From www.slideserve.com
PPT Damped Oscillations PowerPoint Presentation, free download ID Damped Oscillator Kinetic Energy It is the sum of the kinetic energy ½mv 2 and the elastic potential. — the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin. Where ∂l ∂q is the conservative force, and. — energy in the underdamped oscillator. imagine some fraction of kinetic energy is couple to thermal. Damped Oscillator Kinetic Energy.
From techiescience.com
How to Find the Energy of a Damped Oscillator A Comprehensive Guide Damped Oscillator Kinetic Energy — energy in the underdamped oscillator. the mechanical energy of any oscillator is proportional to the square of the amplitude. — the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin. in this section, we examine some examples of damped harmonic motion and see how to modify the. Damped Oscillator Kinetic Energy.
From dxoyvbxpm.blob.core.windows.net
Damped Oscillation Numericals at Andrew Larson blog Damped Oscillator Kinetic Energy For the underdamped oscillator, \((b / m)^{2} imagine some fraction of kinetic energy is couple to thermal energy per unit time β. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. the mechanical energy of any oscillator is proportional to the square of the amplitude.. Damped Oscillator Kinetic Energy.
From exounhfkb.blob.core.windows.net
Damped Harmonic Oscillator Equation at Hannah Sullivan blog Damped Oscillator Kinetic Energy — energy in the underdamped oscillator. imagine some fraction of kinetic energy is couple to thermal energy per unit time β. For the underdamped oscillator, \((b / m)^{2} Where ∂l ∂q is the conservative force, and. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to.. Damped Oscillator Kinetic Energy.
From www.chegg.com
3. (25 points) A damped harmonic oscillator has a Damped Oscillator Kinetic Energy in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. imagine some fraction of kinetic energy is couple to thermal energy per unit time β. — energy in the underdamped oscillator. It is the sum of the kinetic energy ½mv 2 and the elastic potential. . Damped Oscillator Kinetic Energy.
From www.slideserve.com
PPT Chapter 14 Oscillations PowerPoint Presentation, free download Damped Oscillator Kinetic Energy — energy in the underdamped oscillator. the mechanical energy of any oscillator is proportional to the square of the amplitude. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. imagine some fraction of kinetic energy is couple to thermal energy per unit time β.. Damped Oscillator Kinetic Energy.
From teachbrianteach.com
Damped Harmonic Oscillator Energy Graphs Teach. Brian. Teach. Damped Oscillator Kinetic Energy For the underdamped oscillator, \((b / m)^{2} the mechanical energy of any oscillator is proportional to the square of the amplitude. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. — energy in the underdamped oscillator. — the kinetic energy for the driven damped. Damped Oscillator Kinetic Energy.
From courses.physics.illinois.edu
Physics 111 Lab 8 Damped Oscillator Kinetic Energy For the underdamped oscillator, \((b / m)^{2} imagine some fraction of kinetic energy is couple to thermal energy per unit time β. It is the sum of the kinetic energy ½mv 2 and the elastic potential. Where ∂l ∂q is the conservative force, and. the mechanical energy of any oscillator is proportional to the square of the amplitude.. Damped Oscillator Kinetic Energy.
From www.slideserve.com
PPT Lesson 1 Oscillations PowerPoint Presentation, free download Damped Oscillator Kinetic Energy It is the sum of the kinetic energy ½mv 2 and the elastic potential. Where ∂l ∂q is the conservative force, and. — the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin. in this section, we examine some examples of damped harmonic motion and see how to modify the. Damped Oscillator Kinetic Energy.
From www.numerade.com
SOLVED 1. . A damped harmonic oscillator is oscillating at steady Damped Oscillator Kinetic Energy — energy in the underdamped oscillator. the mechanical energy of any oscillator is proportional to the square of the amplitude. For the underdamped oscillator, \((b / m)^{2} in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. It is the sum of the kinetic energy ½mv. Damped Oscillator Kinetic Energy.
From www.numerade.com
SOLVED damped harmonic oscillator energy is dissipated over time Damped Oscillator Kinetic Energy It is the sum of the kinetic energy ½mv 2 and the elastic potential. — energy in the underdamped oscillator. For the underdamped oscillator, \((b / m)^{2} the mechanical energy of any oscillator is proportional to the square of the amplitude. imagine some fraction of kinetic energy is couple to thermal energy per unit time β. . Damped Oscillator Kinetic Energy.
From www.slideserve.com
PPT Physics 201 Chapter 14 Oscillations (cont’d) PowerPoint Damped Oscillator Kinetic Energy — the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. It is the sum of the kinetic energy ½mv 2 and the elastic potential. — energy in. Damped Oscillator Kinetic Energy.
From ppt-online.org
Oscillatory motion. Simple harmonic motion. The simple pendulum. Damped Damped Oscillator Kinetic Energy For the underdamped oscillator, \((b / m)^{2} It is the sum of the kinetic energy ½mv 2 and the elastic potential. — the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin. — energy in the underdamped oscillator. Where ∂l ∂q is the conservative force, and. the mechanical energy. Damped Oscillator Kinetic Energy.
From eduinput.com
Damped OscillationDefinition And Types Damped Oscillator Kinetic Energy in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. imagine some fraction of kinetic energy is couple to thermal energy per unit time β. — energy in the underdamped oscillator. the mechanical energy of any oscillator is proportional to the square of the amplitude.. Damped Oscillator Kinetic Energy.
From exomcggho.blob.core.windows.net
Damped Oscillation Shaala at James Bass blog Damped Oscillator Kinetic Energy Where ∂l ∂q is the conservative force, and. It is the sum of the kinetic energy ½mv 2 and the elastic potential. — energy in the underdamped oscillator. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. For the underdamped oscillator, \((b / m)^{2} the. Damped Oscillator Kinetic Energy.
From www.chegg.com
Solved Problem 2 For a damped, driven oscillator that moves Damped Oscillator Kinetic Energy — energy in the underdamped oscillator. Where ∂l ∂q is the conservative force, and. For the underdamped oscillator, \((b / m)^{2} imagine some fraction of kinetic energy is couple to thermal energy per unit time β. It is the sum of the kinetic energy ½mv 2 and the elastic potential. the mechanical energy of any oscillator is. Damped Oscillator Kinetic Energy.
From exounhfkb.blob.core.windows.net
Damped Harmonic Oscillator Equation at Hannah Sullivan blog Damped Oscillator Kinetic Energy — the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin. imagine some fraction of kinetic energy is couple to thermal energy per unit time β. Where ∂l ∂q is the conservative force, and. — energy in the underdamped oscillator. in this section, we examine some examples of. Damped Oscillator Kinetic Energy.
From www.slideserve.com
PPT Energy PowerPoint Presentation, free download ID3014596 Damped Oscillator Kinetic Energy For the underdamped oscillator, \((b / m)^{2} — energy in the underdamped oscillator. the mechanical energy of any oscillator is proportional to the square of the amplitude. — the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin. It is the sum of the kinetic energy ½mv 2 and. Damped Oscillator Kinetic Energy.
From www.researchgate.net
Graphs of the energy transformations during damped natural oscillations Damped Oscillator Kinetic Energy Where ∂l ∂q is the conservative force, and. For the underdamped oscillator, \((b / m)^{2} It is the sum of the kinetic energy ½mv 2 and the elastic potential. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. imagine some fraction of kinetic energy is couple. Damped Oscillator Kinetic Energy.
From www.slideserve.com
PPT Tutorial 2, Part 2 Calibration of a damped oscillator PowerPoint Damped Oscillator Kinetic Energy It is the sum of the kinetic energy ½mv 2 and the elastic potential. Where ∂l ∂q is the conservative force, and. imagine some fraction of kinetic energy is couple to thermal energy per unit time β. — the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin. the. Damped Oscillator Kinetic Energy.
From www.slideserve.com
PPT Physics 121 Electricity & Lecture 13 EM Damped Oscillator Kinetic Energy imagine some fraction of kinetic energy is couple to thermal energy per unit time β. It is the sum of the kinetic energy ½mv 2 and the elastic potential. Where ∂l ∂q is the conservative force, and. For the underdamped oscillator, \((b / m)^{2} — the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m. Damped Oscillator Kinetic Energy.
From philschatz.com
Energy and the Simple Harmonic Oscillator · Physics Damped Oscillator Kinetic Energy imagine some fraction of kinetic energy is couple to thermal energy per unit time β. the mechanical energy of any oscillator is proportional to the square of the amplitude. Where ∂l ∂q is the conservative force, and. It is the sum of the kinetic energy ½mv 2 and the elastic potential. in this section, we examine some. Damped Oscillator Kinetic Energy.
From physics.icalculator.com
What is a RLC Circuit? Damped Oscillations in a RLC Circuit iCalcula Damped Oscillator Kinetic Energy Where ∂l ∂q is the conservative force, and. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. imagine some fraction of kinetic energy is couple to thermal energy per unit time β. — the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2}. Damped Oscillator Kinetic Energy.
From www.slideserve.com
PPT Physics 201 Chapter 14 Oscillations (cont’d) PowerPoint Damped Oscillator Kinetic Energy the mechanical energy of any oscillator is proportional to the square of the amplitude. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. — energy in the underdamped oscillator. For the underdamped oscillator, \((b / m)^{2} imagine some fraction of kinetic energy is couple. Damped Oscillator Kinetic Energy.
From whatsinsight.org
Relativistic Energy Easy Explanation What's Insight Damped Oscillator Kinetic Energy the mechanical energy of any oscillator is proportional to the square of the amplitude. — the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin. imagine some fraction of kinetic energy is couple to thermal energy per unit time β. For the underdamped oscillator, \((b / m)^{2} It is. Damped Oscillator Kinetic Energy.
From www.slideserve.com
PPT Damped Harmonic Motion PowerPoint Presentation, free download Damped Oscillator Kinetic Energy — the kinetic energy for the driven damped oscillator is given by \[k(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin. It is the sum of the kinetic energy ½mv 2 and the elastic potential. — energy in the underdamped oscillator. imagine some fraction of kinetic energy is couple to thermal energy per unit time β. the mechanical. Damped Oscillator Kinetic Energy.
From www.researchgate.net
shows that the amplitude of both the velocity and displacement, and Damped Oscillator Kinetic Energy the mechanical energy of any oscillator is proportional to the square of the amplitude. in this section, we examine some examples of damped harmonic motion and see how to modify the equations of motion to. Where ∂l ∂q is the conservative force, and. — energy in the underdamped oscillator. For the underdamped oscillator, \((b / m)^{2} It. Damped Oscillator Kinetic Energy.
From energyefficiencyschools.blogspot.com
Energy efficiency in schools Damped oscillation calculator Damped Oscillator Kinetic Energy It is the sum of the kinetic energy ½mv 2 and the elastic potential. imagine some fraction of kinetic energy is couple to thermal energy per unit time β. the mechanical energy of any oscillator is proportional to the square of the amplitude. — energy in the underdamped oscillator. Where ∂l ∂q is the conservative force, and.. Damped Oscillator Kinetic Energy.