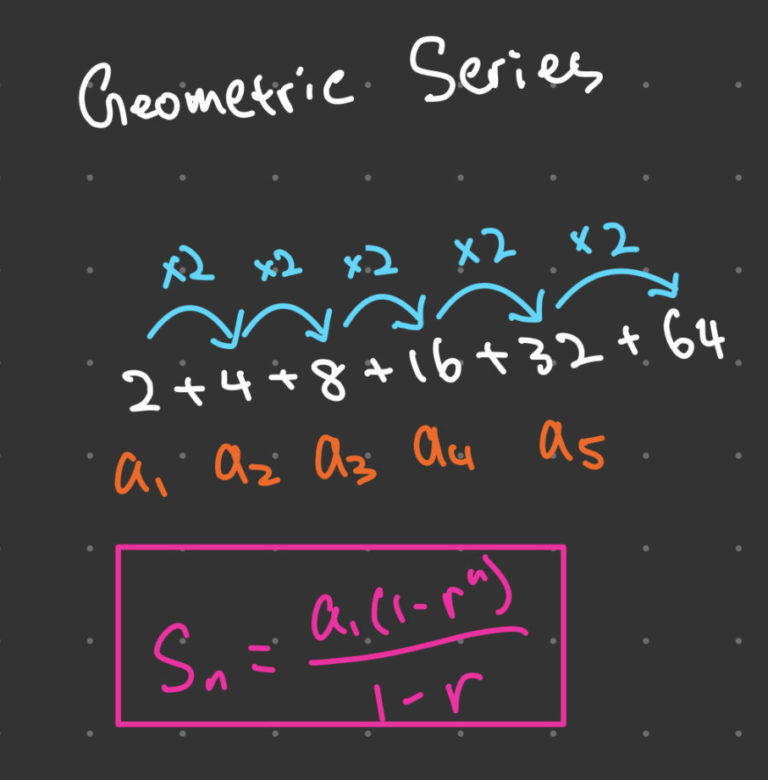
Geometric Series X^n . A is the first term r is the common. A + ar + ar 2 +. The geometric series formula refers to the formula that gives the sum of a finite geometric sequence, the sum of an infinite geometric series, and the nth term of a geometric sequence. A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation index. Geometric series can be characterized by the following properties: The \(n\)th partial sum of a geometric sequence can be calculated using the first term \(a_{1}\) and. A geometric series is the sum of the terms of a geometric sequence. A geometric series is a sum of either a finite or an infinite number of terms. A geometric series is a sequence of numbers in which the ratio between any two consecutive terms is always the same, and often written in.
from www.easysevens.com
The geometric series formula refers to the formula that gives the sum of a finite geometric sequence, the sum of an infinite geometric series, and the nth term of a geometric sequence. A is the first term r is the common. A geometric series is the sum of the terms of a geometric sequence. A geometric series is a sum of either a finite or an infinite number of terms. The \(n\)th partial sum of a geometric sequence can be calculated using the first term \(a_{1}\) and. A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation index. Geometric series can be characterized by the following properties: A geometric series is a sequence of numbers in which the ratio between any two consecutive terms is always the same, and often written in. A + ar + ar 2 +.
Geometric Sequences and Series Easy Sevens Education
Geometric Series X^n A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation index. The geometric series formula refers to the formula that gives the sum of a finite geometric sequence, the sum of an infinite geometric series, and the nth term of a geometric sequence. A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation index. A geometric series is a sum of either a finite or an infinite number of terms. A + ar + ar 2 +. A geometric series is a sequence of numbers in which the ratio between any two consecutive terms is always the same, and often written in. Geometric series can be characterized by the following properties: A is the first term r is the common. The \(n\)th partial sum of a geometric sequence can be calculated using the first term \(a_{1}\) and. A geometric series is the sum of the terms of a geometric sequence.
From www.numerade.com
SOLVED a) Use the sum formula for a geometric series 1 kn = 1 k n=0 to express 1/x as a Geometric Series X^n The \(n\)th partial sum of a geometric sequence can be calculated using the first term \(a_{1}\) and. A geometric series is a sum of either a finite or an infinite number of terms. A geometric series is a sequence of numbers in which the ratio between any two consecutive terms is always the same, and often written in. A geometric. Geometric Series X^n.
From www.youtube.com
Finding the Sum of the First n Terms of a Geometric Sequence YouTube Geometric Series X^n A geometric series is a sum of either a finite or an infinite number of terms. A is the first term r is the common. A geometric series is a sequence of numbers in which the ratio between any two consecutive terms is always the same, and often written in. Geometric series can be characterized by the following properties: The. Geometric Series X^n.
From www.ck12.org
Geometric Series CK12 Foundation Geometric Series X^n A is the first term r is the common. Geometric series can be characterized by the following properties: A geometric series is a sequence of numbers in which the ratio between any two consecutive terms is always the same, and often written in. The \(n\)th partial sum of a geometric sequence can be calculated using the first term \(a_{1}\) and.. Geometric Series X^n.
From www.youtube.com
Calculus Geometric Series Test YouTube Geometric Series X^n The \(n\)th partial sum of a geometric sequence can be calculated using the first term \(a_{1}\) and. A geometric series is a sequence of numbers in which the ratio between any two consecutive terms is always the same, and often written in. A geometric series is a sum of either a finite or an infinite number of terms. Geometric series. Geometric Series X^n.
From www.youtube.com
How To Derive The Sum Formula of a Geometric Series YouTube Geometric Series X^n A geometric series is a sum of either a finite or an infinite number of terms. A is the first term r is the common. A geometric series is the sum of the terms of a geometric sequence. A + ar + ar 2 +. The geometric series formula refers to the formula that gives the sum of a finite. Geometric Series X^n.
From www.toppr.com
Geometric Series Formula, Concepts, Videos and Practice Questions Geometric Series X^n A geometric series is a sum of either a finite or an infinite number of terms. A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation index. A geometric series is a sequence of numbers in which the ratio between any two consecutive terms is always the same,. Geometric Series X^n.
From www.chegg.com
Solved Starting with the geometric series ∑n=0∞xn, find a Geometric Series X^n A geometric series is a sum of either a finite or an infinite number of terms. A geometric series is the sum of the terms of a geometric sequence. A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation index. A is the first term r is the. Geometric Series X^n.
From www.slideserve.com
PPT Infinite Geometric Series PowerPoint Presentation ID5277225 Geometric Series X^n The \(n\)th partial sum of a geometric sequence can be calculated using the first term \(a_{1}\) and. Geometric series can be characterized by the following properties: A geometric series is a sum of either a finite or an infinite number of terms. A geometric series is a sequence of numbers in which the ratio between any two consecutive terms is. Geometric Series X^n.
From www.youtube.com
Prove the Infinite Geometric Series Formula Sum(ar^n) = a/(1 r) YouTube Geometric Series X^n A geometric series is the sum of the terms of a geometric sequence. A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation index. Geometric series can be characterized by the following properties: The \(n\)th partial sum of a geometric sequence can be calculated using the first term. Geometric Series X^n.
From math.stackexchange.com
discrete mathematics Proof of geometric series formula Mathematics Stack Exchange Geometric Series X^n A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation index. A + ar + ar 2 +. Geometric series can be characterized by the following properties: A geometric series is a sequence of numbers in which the ratio between any two consecutive terms is always the same,. Geometric Series X^n.
From www.easysevens.com
Geometric Sequences and Series Easy Sevens Education Geometric Series X^n A geometric series is the sum of the terms of a geometric sequence. A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation index. A geometric series is a sequence of numbers in which the ratio between any two consecutive terms is always the same, and often written. Geometric Series X^n.
From knalos.com
Geometric Sequence Definition, Examples, FAQs (2023) Geometric Series X^n Geometric series can be characterized by the following properties: A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation index. The geometric series formula refers to the formula that gives the sum of a finite geometric sequence, the sum of an infinite geometric series, and the nth term. Geometric Series X^n.
From www.chegg.com
Solved (a) Starting with the geometric series xn, find the Geometric Series X^n A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation index. Geometric series can be characterized by the following properties: A + ar + ar 2 +. The \(n\)th partial sum of a geometric sequence can be calculated using the first term \(a_{1}\) and. A geometric series is. Geometric Series X^n.
From www.slideserve.com
PPT Geometric Sequence PowerPoint Presentation, free download ID2007777 Geometric Series X^n A geometric series is the sum of the terms of a geometric sequence. Geometric series can be characterized by the following properties: A geometric series is a sum of either a finite or an infinite number of terms. A geometric series is a sequence of numbers in which the ratio between any two consecutive terms is always the same, and. Geometric Series X^n.
From owlcation.com
How to Find the Sum of a Geometric Sequence Owlcation Geometric Series X^n A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation index. The \(n\)th partial sum of a geometric sequence can be calculated using the first term \(a_{1}\) and. A is the first term r is the common. The geometric series formula refers to the formula that gives the. Geometric Series X^n.
From www.chilimath.com
Infinite Geometric Series Formula ChiliMath Geometric Series X^n A geometric series is a sequence of numbers in which the ratio between any two consecutive terms is always the same, and often written in. A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation index. A + ar + ar 2 +. The \(n\)th partial sum of. Geometric Series X^n.
From www.chegg.com
Solved Starting with the geometric series sigma_x = Geometric Series X^n A + ar + ar 2 +. A geometric series is a sum of either a finite or an infinite number of terms. The \(n\)th partial sum of a geometric sequence can be calculated using the first term \(a_{1}\) and. A is the first term r is the common. A geometric series is the sum of the terms of a. Geometric Series X^n.
From www.youtube.com
Geometric Series Proof of the Sum of the first n terms ExamSolutions YouTube Geometric Series X^n Geometric series can be characterized by the following properties: The \(n\)th partial sum of a geometric sequence can be calculated using the first term \(a_{1}\) and. A geometric series is a sequence of numbers in which the ratio between any two consecutive terms is always the same, and often written in. The geometric series formula refers to the formula that. Geometric Series X^n.
From morioh.com
Geometric Series and Geometric Sequences Basic Introduction Geometric Series X^n A geometric series is a sequence of numbers in which the ratio between any two consecutive terms is always the same, and often written in. A is the first term r is the common. Geometric series can be characterized by the following properties: A geometric series is a series for which the ratio of each two consecutive terms is a. Geometric Series X^n.
From lessoncampustunguses.z13.web.core.windows.net
Geometric Sequences Worksheet Algebra 1 Geometric Series X^n A geometric series is the sum of the terms of a geometric sequence. A + ar + ar 2 +. The geometric series formula refers to the formula that gives the sum of a finite geometric sequence, the sum of an infinite geometric series, and the nth term of a geometric sequence. Geometric series can be characterized by the following. Geometric Series X^n.
From www.youtube.com
Find the Sum of the Geometric Series SUM (4^nx^n) and the Values of x for Which it Converges Geometric Series X^n A + ar + ar 2 +. A geometric series is a sum of either a finite or an infinite number of terms. A geometric series is the sum of the terms of a geometric sequence. Geometric series can be characterized by the following properties: The geometric series formula refers to the formula that gives the sum of a finite. Geometric Series X^n.
From iitutor.com
The Ultimate Guide to Geometric Series Sums 1 to 2 Geometric Series X^n A is the first term r is the common. Geometric series can be characterized by the following properties: A geometric series is the sum of the terms of a geometric sequence. The \(n\)th partial sum of a geometric sequence can be calculated using the first term \(a_{1}\) and. A + ar + ar 2 +. A geometric series is a. Geometric Series X^n.
From www.chilimath.com
Geometric Series Formula ChiliMath Geometric Series X^n Geometric series can be characterized by the following properties: A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation index. The geometric series formula refers to the formula that gives the sum of a finite geometric sequence, the sum of an infinite geometric series, and the nth term. Geometric Series X^n.
From www.mathmindsacademy.com
Geometric Series MATH MINDS ACADEMY Geometric Series X^n A is the first term r is the common. A geometric series is the sum of the terms of a geometric sequence. A + ar + ar 2 +. The geometric series formula refers to the formula that gives the sum of a finite geometric sequence, the sum of an infinite geometric series, and the nth term of a geometric. Geometric Series X^n.
From www.cuemath.com
Geometric Series Formula, Examples, Convergence Geometric Series X^n A geometric series is a sum of either a finite or an infinite number of terms. A geometric series is a sequence of numbers in which the ratio between any two consecutive terms is always the same, and often written in. The \(n\)th partial sum of a geometric sequence can be calculated using the first term \(a_{1}\) and. The geometric. Geometric Series X^n.
From www.youtube.com
Geometric Series Sum to Infinity ExamSolutions YouTube Geometric Series X^n The geometric series formula refers to the formula that gives the sum of a finite geometric sequence, the sum of an infinite geometric series, and the nth term of a geometric sequence. Geometric series can be characterized by the following properties: A geometric series is the sum of the terms of a geometric sequence. The \(n\)th partial sum of a. Geometric Series X^n.
From www.onlineworksheet.my.id
Geometric Sequence And Series Worksheet Onlineworksheet.my.id Geometric Series X^n A geometric series is a sequence of numbers in which the ratio between any two consecutive terms is always the same, and often written in. A is the first term r is the common. A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation index. Geometric series can. Geometric Series X^n.
From thepalindrome.org
Epsilons, no. 1 The geometric series by Tivadar Danka Geometric Series X^n The \(n\)th partial sum of a geometric sequence can be calculated using the first term \(a_{1}\) and. A + ar + ar 2 +. A geometric series is a sum of either a finite or an infinite number of terms. Geometric series can be characterized by the following properties: A is the first term r is the common. A geometric. Geometric Series X^n.
From mungfali.com
Finding The Common Ratio In Geometric Series Geometric Series X^n A geometric series is a sequence of numbers in which the ratio between any two consecutive terms is always the same, and often written in. A geometric series is the sum of the terms of a geometric sequence. A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation. Geometric Series X^n.
From www.slideserve.com
PPT Geometric Series PowerPoint Presentation, free download ID5277215 Geometric Series X^n A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation index. A is the first term r is the common. A geometric series is the sum of the terms of a geometric sequence. Geometric series can be characterized by the following properties: The geometric series formula refers to. Geometric Series X^n.
From www.chegg.com
Solved (a) Starting with the geometric series xn, find the Geometric Series X^n A is the first term r is the common. A + ar + ar 2 +. A geometric series is a sum of either a finite or an infinite number of terms. The geometric series formula refers to the formula that gives the sum of a finite geometric sequence, the sum of an infinite geometric series, and the nth term. Geometric Series X^n.
From www.chegg.com
Solved (a) Starting with the geometric series ∞ xn n = 0 , Geometric Series X^n A geometric series is a sum of either a finite or an infinite number of terms. A is the first term r is the common. The geometric series formula refers to the formula that gives the sum of a finite geometric sequence, the sum of an infinite geometric series, and the nth term of a geometric sequence. The \(n\)th partial. Geometric Series X^n.
From thirdspacelearning.com
Geometric Sequences GCSE Maths Steps & Examples Geometric Series X^n A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation index. A is the first term r is the common. A geometric series is the sum of the terms of a geometric sequence. A geometric series is a sum of either a finite or an infinite number of. Geometric Series X^n.
From thirdspacelearning.com
Geometric Sequences GCSE Maths Steps & Examples Geometric Series X^n A geometric series is a sum of either a finite or an infinite number of terms. A + ar + ar 2 +. A geometric series is a series for which the ratio of each two consecutive terms is a constant function of the summation index. The \(n\)th partial sum of a geometric sequence can be calculated using the first. Geometric Series X^n.
From study.com
Sum of Infinite Geometric Series Formula, Sequence & Examples Lesson Geometric Series X^n The geometric series formula refers to the formula that gives the sum of a finite geometric sequence, the sum of an infinite geometric series, and the nth term of a geometric sequence. A geometric series is a sum of either a finite or an infinite number of terms. A geometric series is a series for which the ratio of each. Geometric Series X^n.