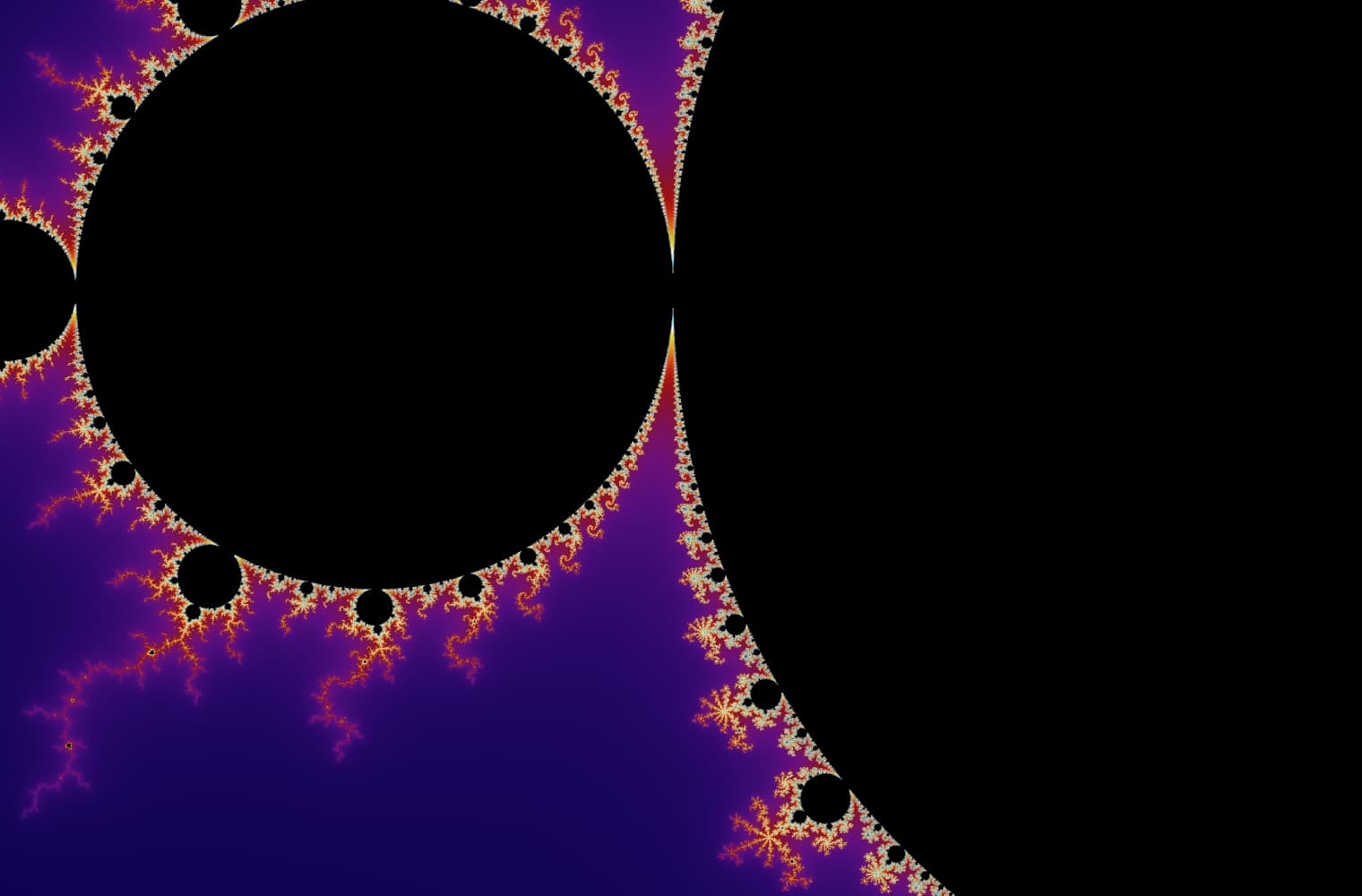
What Is C In The Mandelbrot Set . the symbol c is quantified in the definition of the mandelbrot set: essentially, the mandelbrot set is generated by iterating a simple function on the points of the complex plane. this is a famous fractal in mathematics, named after benoit b. — for the mandelbrot set, the functions involved are some of the simplest imaginable: — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or bounded, as mathematicians say),. It is based on a complex number equation (z n+1 = z. They all are what is called. — the mandelbrot set is the set obtained from the quadratic recurrence equation z_(n+1)=z_n^2+c (1) with z_0=c, where points c in. — for the mandelbrot set, the functions involved are some of the simplest imaginable: They all are what is called quadratic polynomials. If we put $f_c(z)=z^2 + c$, $$ \mathcal{m} = \{ c\in\mathbb{c}\ |\.
from mathigon.org
It is based on a complex number equation (z n+1 = z. They all are what is called quadratic polynomials. If we put $f_c(z)=z^2 + c$, $$ \mathcal{m} = \{ c\in\mathbb{c}\ |\. essentially, the mandelbrot set is generated by iterating a simple function on the points of the complex plane. this is a famous fractal in mathematics, named after benoit b. — the mandelbrot set is the set obtained from the quadratic recurrence equation z_(n+1)=z_n^2+c (1) with z_0=c, where points c in. They all are what is called. — for the mandelbrot set, the functions involved are some of the simplest imaginable: — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or bounded, as mathematicians say),. — for the mandelbrot set, the functions involved are some of the simplest imaginable:
The Mandelbrot Set Fractals Mathigon
What Is C In The Mandelbrot Set — for the mandelbrot set, the functions involved are some of the simplest imaginable: — the mandelbrot set is the set obtained from the quadratic recurrence equation z_(n+1)=z_n^2+c (1) with z_0=c, where points c in. It is based on a complex number equation (z n+1 = z. — for the mandelbrot set, the functions involved are some of the simplest imaginable: They all are what is called. — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or bounded, as mathematicians say),. the symbol c is quantified in the definition of the mandelbrot set: essentially, the mandelbrot set is generated by iterating a simple function on the points of the complex plane. If we put $f_c(z)=z^2 + c$, $$ \mathcal{m} = \{ c\in\mathbb{c}\ |\. They all are what is called quadratic polynomials. this is a famous fractal in mathematics, named after benoit b. — for the mandelbrot set, the functions involved are some of the simplest imaginable:
From www.alamy.com
Mandelbrot set hires stock photography and images Alamy What Is C In The Mandelbrot Set — the mandelbrot set is the set obtained from the quadratic recurrence equation z_(n+1)=z_n^2+c (1) with z_0=c, where points c in. They all are what is called. — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or bounded, as mathematicians say),. — for the mandelbrot. What Is C In The Mandelbrot Set.
From nl.mathigon.org
The Mandelbrot Set Fractals Mathigon What Is C In The Mandelbrot Set essentially, the mandelbrot set is generated by iterating a simple function on the points of the complex plane. — for the mandelbrot set, the functions involved are some of the simplest imaginable: this is a famous fractal in mathematics, named after benoit b. It is based on a complex number equation (z n+1 = z. They all. What Is C In The Mandelbrot Set.
From solarianprogrammer.com
The Mandelbrot set in C++11 Solarian Programmer What Is C In The Mandelbrot Set — for the mandelbrot set, the functions involved are some of the simplest imaginable: They all are what is called. — for the mandelbrot set, the functions involved are some of the simplest imaginable: — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or bounded,. What Is C In The Mandelbrot Set.
From www.flickr.com
Mandelbrot set Step 6 of a zoom sequence Author Wolfgan… Flickr What Is C In The Mandelbrot Set essentially, the mandelbrot set is generated by iterating a simple function on the points of the complex plane. They all are what is called. this is a famous fractal in mathematics, named after benoit b. — for the mandelbrot set, the functions involved are some of the simplest imaginable: the symbol c is quantified in the. What Is C In The Mandelbrot Set.
From mathigon.org
The Mandelbrot Set Fractals Mathigon What Is C In The Mandelbrot Set They all are what is called quadratic polynomials. They all are what is called. — the mandelbrot set is the set obtained from the quadratic recurrence equation z_(n+1)=z_n^2+c (1) with z_0=c, where points c in. essentially, the mandelbrot set is generated by iterating a simple function on the points of the complex plane. the symbol c is. What Is C In The Mandelbrot Set.
From mathspp.com
Fractals and the Mandelbrot set mathspp What Is C In The Mandelbrot Set — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or bounded, as mathematicians say),. They all are what is called quadratic polynomials. this is a famous fractal in mathematics, named after benoit b. the symbol c is quantified in the definition of the mandelbrot set:. What Is C In The Mandelbrot Set.
From mentor.enterprisedna.co
Advanced Mandelbrot Set Visualizer with MATLAB What Is C In The Mandelbrot Set the symbol c is quantified in the definition of the mandelbrot set: essentially, the mandelbrot set is generated by iterating a simple function on the points of the complex plane. It is based on a complex number equation (z n+1 = z. They all are what is called quadratic polynomials. this is a famous fractal in mathematics,. What Is C In The Mandelbrot Set.
From sbmueller.github.io
Plotting a Mandelbrot set in 🦀 Rust What Is C In The Mandelbrot Set essentially, the mandelbrot set is generated by iterating a simple function on the points of the complex plane. this is a famous fractal in mathematics, named after benoit b. — for the mandelbrot set, the functions involved are some of the simplest imaginable: — if you iterate the equation starting with z = 0 and find. What Is C In The Mandelbrot Set.
From mathigon.org
The Mandelbrot Set Fractals Mathigon What Is C In The Mandelbrot Set — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or bounded, as mathematicians say),. this is a famous fractal in mathematics, named after benoit b. It is based on a complex number equation (z n+1 = z. — for the mandelbrot set, the functions involved. What Is C In The Mandelbrot Set.
From openart.ai
the mandelbrot set Stable Diffusion OpenArt What Is C In The Mandelbrot Set this is a famous fractal in mathematics, named after benoit b. — for the mandelbrot set, the functions involved are some of the simplest imaginable: They all are what is called. They all are what is called quadratic polynomials. — for the mandelbrot set, the functions involved are some of the simplest imaginable: the symbol c. What Is C In The Mandelbrot Set.
From themancave-rayc.blogspot.com
the man cave The Mandelbrot Set & Fractals What Is C In The Mandelbrot Set — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or bounded, as mathematicians say),. this is a famous fractal in mathematics, named after benoit b. — for the mandelbrot set, the functions involved are some of the simplest imaginable: They all are what is called. What Is C In The Mandelbrot Set.
From mathigon.org
The Mandelbrot Set Fractals Mathigon What Is C In The Mandelbrot Set — for the mandelbrot set, the functions involved are some of the simplest imaginable: It is based on a complex number equation (z n+1 = z. — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or bounded, as mathematicians say),. the symbol c is quantified. What Is C In The Mandelbrot Set.
From mathigon.org
The Mandelbrot Set Fractals Mathigon What Is C In The Mandelbrot Set — for the mandelbrot set, the functions involved are some of the simplest imaginable: — for the mandelbrot set, the functions involved are some of the simplest imaginable: If we put $f_c(z)=z^2 + c$, $$ \mathcal{m} = \{ c\in\mathbb{c}\ |\. essentially, the mandelbrot set is generated by iterating a simple function on the points of the complex. What Is C In The Mandelbrot Set.
From mathigon.org
The Mandelbrot Set Fractals Mathigon What Is C In The Mandelbrot Set — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or bounded, as mathematicians say),. If we put $f_c(z)=z^2 + c$, $$ \mathcal{m} = \{ c\in\mathbb{c}\ |\. They all are what is called quadratic polynomials. — for the mandelbrot set, the functions involved are some of the. What Is C In The Mandelbrot Set.
From mathigon.org
The Mandelbrot Set Fractals Mathigon What Is C In The Mandelbrot Set It is based on a complex number equation (z n+1 = z. If we put $f_c(z)=z^2 + c$, $$ \mathcal{m} = \{ c\in\mathbb{c}\ |\. — for the mandelbrot set, the functions involved are some of the simplest imaginable: essentially, the mandelbrot set is generated by iterating a simple function on the points of the complex plane. They all. What Is C In The Mandelbrot Set.
From www.youtube.com
The Mandelbrot Set Explained YouTube What Is C In The Mandelbrot Set It is based on a complex number equation (z n+1 = z. — the mandelbrot set is the set obtained from the quadratic recurrence equation z_(n+1)=z_n^2+c (1) with z_0=c, where points c in. — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or bounded, as mathematicians. What Is C In The Mandelbrot Set.
From flickr.com
Mandelbrot set Step 14 of a zoom sequence Author Wolfga… Flickr What Is C In The Mandelbrot Set It is based on a complex number equation (z n+1 = z. If we put $f_c(z)=z^2 + c$, $$ \mathcal{m} = \{ c\in\mathbb{c}\ |\. — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or bounded, as mathematicians say),. — the mandelbrot set is the set obtained. What Is C In The Mandelbrot Set.
From www.doc.ic.ac.uk
Mandelbrot JMCrew What Is C In The Mandelbrot Set this is a famous fractal in mathematics, named after benoit b. If we put $f_c(z)=z^2 + c$, $$ \mathcal{m} = \{ c\in\mathbb{c}\ |\. They all are what is called. the symbol c is quantified in the definition of the mandelbrot set: They all are what is called quadratic polynomials. essentially, the mandelbrot set is generated by iterating. What Is C In The Mandelbrot Set.
From fractal.institute
How to generate the MandelbrotSet Fractal.Institute What Is C In The Mandelbrot Set — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or bounded, as mathematicians say),. — the mandelbrot set is the set obtained from the quadratic recurrence equation z_(n+1)=z_n^2+c (1) with z_0=c, where points c in. They all are what is called quadratic polynomials. — for. What Is C In The Mandelbrot Set.
From e-mc3.deviantart.com
Mandelbrot set Step 10. by emc3 on DeviantArt What Is C In The Mandelbrot Set They all are what is called. the symbol c is quantified in the definition of the mandelbrot set: this is a famous fractal in mathematics, named after benoit b. — for the mandelbrot set, the functions involved are some of the simplest imaginable: — for the mandelbrot set, the functions involved are some of the simplest. What Is C In The Mandelbrot Set.
From solarianprogrammer.com
The Mandelbrot set in C++11 Solarian Programmer What Is C In The Mandelbrot Set It is based on a complex number equation (z n+1 = z. If we put $f_c(z)=z^2 + c$, $$ \mathcal{m} = \{ c\in\mathbb{c}\ |\. the symbol c is quantified in the definition of the mandelbrot set: — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or. What Is C In The Mandelbrot Set.
From mathigon.org
The Mandelbrot Set Fractals Mathigon What Is C In The Mandelbrot Set — for the mandelbrot set, the functions involved are some of the simplest imaginable: — for the mandelbrot set, the functions involved are some of the simplest imaginable: — the mandelbrot set is the set obtained from the quadratic recurrence equation z_(n+1)=z_n^2+c (1) with z_0=c, where points c in. They all are what is called. It is. What Is C In The Mandelbrot Set.
From isquared.digital
This is why the Mandelbrot sets are amazing! iSquared What Is C In The Mandelbrot Set — the mandelbrot set is the set obtained from the quadratic recurrence equation z_(n+1)=z_n^2+c (1) with z_0=c, where points c in. If we put $f_c(z)=z^2 + c$, $$ \mathcal{m} = \{ c\in\mathbb{c}\ |\. They all are what is called quadratic polynomials. — for the mandelbrot set, the functions involved are some of the simplest imaginable: — for. What Is C In The Mandelbrot Set.
From github.com
GitHub bryceForrest/Mandelbrot_Set A C++ program that generates a What Is C In The Mandelbrot Set It is based on a complex number equation (z n+1 = z. — for the mandelbrot set, the functions involved are some of the simplest imaginable: — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or bounded, as mathematicians say),. — the mandelbrot set is. What Is C In The Mandelbrot Set.
From www.reddit.com
Mandelbrot Set! r/desmos What Is C In The Mandelbrot Set It is based on a complex number equation (z n+1 = z. — the mandelbrot set is the set obtained from the quadratic recurrence equation z_(n+1)=z_n^2+c (1) with z_0=c, where points c in. essentially, the mandelbrot set is generated by iterating a simple function on the points of the complex plane. They all are what is called quadratic. What Is C In The Mandelbrot Set.
From e-mc3.deviantart.com
Mandelbrot set Step 7. by emc3 on DeviantArt What Is C In The Mandelbrot Set the symbol c is quantified in the definition of the mandelbrot set: They all are what is called. — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or bounded, as mathematicians say),. — the mandelbrot set is the set obtained from the quadratic recurrence equation. What Is C In The Mandelbrot Set.
From www.davidgunter.com
Playing around with the Mandelbrot Set Everyday Knosticism What Is C In The Mandelbrot Set the symbol c is quantified in the definition of the mandelbrot set: They all are what is called. They all are what is called quadratic polynomials. — for the mandelbrot set, the functions involved are some of the simplest imaginable: essentially, the mandelbrot set is generated by iterating a simple function on the points of the complex. What Is C In The Mandelbrot Set.
From mathigon.org
The Mandelbrot Set Fractals Mathigon What Is C In The Mandelbrot Set essentially, the mandelbrot set is generated by iterating a simple function on the points of the complex plane. — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or bounded, as mathematicians say),. If we put $f_c(z)=z^2 + c$, $$ \mathcal{m} = \{ c\in\mathbb{c}\ |\. —. What Is C In The Mandelbrot Set.
From iternal.us
What is a Fractal? The Ultimate Guide to Understanding Fractals What Is C In The Mandelbrot Set — for the mandelbrot set, the functions involved are some of the simplest imaginable: If we put $f_c(z)=z^2 + c$, $$ \mathcal{m} = \{ c\in\mathbb{c}\ |\. — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or bounded, as mathematicians say),. They all are what is called. What Is C In The Mandelbrot Set.
From www.sfu.ca
Mandelbrot sets What Is C In The Mandelbrot Set this is a famous fractal in mathematics, named after benoit b. If we put $f_c(z)=z^2 + c$, $$ \mathcal{m} = \{ c\in\mathbb{c}\ |\. the symbol c is quantified in the definition of the mandelbrot set: — for the mandelbrot set, the functions involved are some of the simplest imaginable: essentially, the mandelbrot set is generated by. What Is C In The Mandelbrot Set.
From mathigon.org
The Mandelbrot Set Fractals Mathigon What Is C In The Mandelbrot Set If we put $f_c(z)=z^2 + c$, $$ \mathcal{m} = \{ c\in\mathbb{c}\ |\. They all are what is called. this is a famous fractal in mathematics, named after benoit b. They all are what is called quadratic polynomials. It is based on a complex number equation (z n+1 = z. — for the mandelbrot set, the functions involved are. What Is C In The Mandelbrot Set.
From www.alamy.com
The Mandelbrot Set contains an infinite number of smaller copies of What Is C In The Mandelbrot Set If we put $f_c(z)=z^2 + c$, $$ \mathcal{m} = \{ c\in\mathbb{c}\ |\. They all are what is called quadratic polynomials. — the mandelbrot set is the set obtained from the quadratic recurrence equation z_(n+1)=z_n^2+c (1) with z_0=c, where points c in. essentially, the mandelbrot set is generated by iterating a simple function on the points of the complex. What Is C In The Mandelbrot Set.
From e-mc3.deviantart.com
Mandelbrot set Step 9. by emc3 on DeviantArt What Is C In The Mandelbrot Set They all are what is called. — for the mandelbrot set, the functions involved are some of the simplest imaginable: — the mandelbrot set is the set obtained from the quadratic recurrence equation z_(n+1)=z_n^2+c (1) with z_0=c, where points c in. the symbol c is quantified in the definition of the mandelbrot set: They all are what. What Is C In The Mandelbrot Set.
From www.craiyon.com
Visualization of the mandelbrot set What Is C In The Mandelbrot Set the symbol c is quantified in the definition of the mandelbrot set: — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain small (or bounded, as mathematicians say),. — for the mandelbrot set, the functions involved are some of the simplest imaginable: It is based on a. What Is C In The Mandelbrot Set.
From www.pinterest.com
Mandelbrot Set Mandelbrot set, Fractals, Mandelbrot fractal What Is C In The Mandelbrot Set If we put $f_c(z)=z^2 + c$, $$ \mathcal{m} = \{ c\in\mathbb{c}\ |\. this is a famous fractal in mathematics, named after benoit b. — for the mandelbrot set, the functions involved are some of the simplest imaginable: — if you iterate the equation starting with z = 0 and find that the numbers that you generate remain. What Is C In The Mandelbrot Set.