Is A Circle Graph A Function . In mathematical terms, a function is a special type of relationship where each input has a single output. That is, it is an undirected graph whose vertices can be. Notice that the single point. If you want to have a function that draws a circle with radius $r$ and center $p = (x_0, y_0)$ on the cartesian plane, you can use the function $f : You can easily get a function for a circle (yes, a function for a circle) by the function $f:\bbb r \rightarrow \bbb r^2$ defined by $t\,\mapsto\,\,<cos(t),sin(t)>$. A circle on a graph is not considered a function because it fails the vertical line test. The vertical line test states that if a vertical line intersects. No, a circle is not a function. In graph theory, a circle graph is the intersection graph of a chord diagram. A fundamental characteristic of a function in mathematics is that every input is associated with exactly one output. This is often referred to as the vertical.
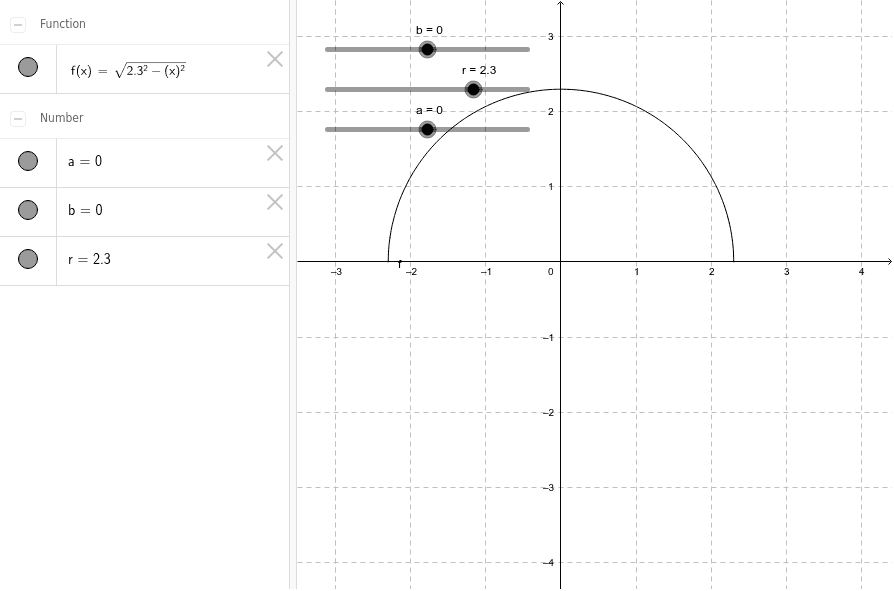
from www.geogebra.org
You can easily get a function for a circle (yes, a function for a circle) by the function $f:\bbb r \rightarrow \bbb r^2$ defined by $t\,\mapsto\,\,<cos(t),sin(t)>$. A fundamental characteristic of a function in mathematics is that every input is associated with exactly one output. The vertical line test states that if a vertical line intersects. In mathematical terms, a function is a special type of relationship where each input has a single output. A circle on a graph is not considered a function because it fails the vertical line test. This is often referred to as the vertical. No, a circle is not a function. If you want to have a function that draws a circle with radius $r$ and center $p = (x_0, y_0)$ on the cartesian plane, you can use the function $f : That is, it is an undirected graph whose vertices can be. Notice that the single point.
Graph of a Semicircular Function GeoGebra
Is A Circle Graph A Function In mathematical terms, a function is a special type of relationship where each input has a single output. A fundamental characteristic of a function in mathematics is that every input is associated with exactly one output. In mathematical terms, a function is a special type of relationship where each input has a single output. If you want to have a function that draws a circle with radius $r$ and center $p = (x_0, y_0)$ on the cartesian plane, you can use the function $f : That is, it is an undirected graph whose vertices can be. No, a circle is not a function. This is often referred to as the vertical. The vertical line test states that if a vertical line intersects. Notice that the single point. In graph theory, a circle graph is the intersection graph of a chord diagram. You can easily get a function for a circle (yes, a function for a circle) by the function $f:\bbb r \rightarrow \bbb r^2$ defined by $t\,\mapsto\,\,<cos(t),sin(t)>$. A circle on a graph is not considered a function because it fails the vertical line test.
From math.stackexchange.com
algebra precalculus Domain of function when open circles are included Is A Circle Graph A Function That is, it is an undirected graph whose vertices can be. A circle on a graph is not considered a function because it fails the vertical line test. No, a circle is not a function. In graph theory, a circle graph is the intersection graph of a chord diagram. A fundamental characteristic of a function in mathematics is that every. Is A Circle Graph A Function.
From www.slideshare.net
Circular functions Is A Circle Graph A Function No, a circle is not a function. A fundamental characteristic of a function in mathematics is that every input is associated with exactly one output. You can easily get a function for a circle (yes, a function for a circle) by the function $f:\bbb r \rightarrow \bbb r^2$ defined by $t\,\mapsto\,\,<cos(t),sin(t)>$. A circle on a graph is not considered a. Is A Circle Graph A Function.
From www.youtube.com
Circle a function? Check domain, range, vertical line test, graph of Is A Circle Graph A Function If you want to have a function that draws a circle with radius $r$ and center $p = (x_0, y_0)$ on the cartesian plane, you can use the function $f : That is, it is an undirected graph whose vertices can be. In mathematical terms, a function is a special type of relationship where each input has a single output.. Is A Circle Graph A Function.
From www.cuemath.com
Unit circle Trigonometric Functions using Unit Circle Unit Circle Is A Circle Graph A Function You can easily get a function for a circle (yes, a function for a circle) by the function $f:\bbb r \rightarrow \bbb r^2$ defined by $t\,\mapsto\,\,<cos(t),sin(t)>$. The vertical line test states that if a vertical line intersects. A fundamental characteristic of a function in mathematics is that every input is associated with exactly one output. Notice that the single point.. Is A Circle Graph A Function.
From owlcation.com
How to Graph a Circle Given a General or Standard Equation Owlcation Is A Circle Graph A Function No, a circle is not a function. In mathematical terms, a function is a special type of relationship where each input has a single output. Notice that the single point. A circle on a graph is not considered a function because it fails the vertical line test. You can easily get a function for a circle (yes, a function for. Is A Circle Graph A Function.
From ximera.osu.edu
The Sine and Cosine Functions Ximera Is A Circle Graph A Function In graph theory, a circle graph is the intersection graph of a chord diagram. You can easily get a function for a circle (yes, a function for a circle) by the function $f:\bbb r \rightarrow \bbb r^2$ defined by $t\,\mapsto\,\,<cos(t),sin(t)>$. In mathematical terms, a function is a special type of relationship where each input has a single output. Notice that. Is A Circle Graph A Function.
From www.geogebra.org
Graph of a Semicircular Function GeoGebra Is A Circle Graph A Function A fundamental characteristic of a function in mathematics is that every input is associated with exactly one output. That is, it is an undirected graph whose vertices can be. A circle on a graph is not considered a function because it fails the vertical line test. This is often referred to as the vertical. The vertical line test states that. Is A Circle Graph A Function.
From theeducationtraining.com
Equation of a circle calculator Is A Circle Graph A Function No, a circle is not a function. A fundamental characteristic of a function in mathematics is that every input is associated with exactly one output. This is often referred to as the vertical. Notice that the single point. In mathematical terms, a function is a special type of relationship where each input has a single output. A circle on a. Is A Circle Graph A Function.
From trigidentities.net
Six Trigonometric Functions Graph Examples Is A Circle Graph A Function Notice that the single point. That is, it is an undirected graph whose vertices can be. If you want to have a function that draws a circle with radius $r$ and center $p = (x_0, y_0)$ on the cartesian plane, you can use the function $f : In mathematical terms, a function is a special type of relationship where each. Is A Circle Graph A Function.
From www.amathsdictionaryforkids.com
circle graph, pie graph, pie chart, sector graph A Maths Dictionary Is A Circle Graph A Function That is, it is an undirected graph whose vertices can be. The vertical line test states that if a vertical line intersects. This is often referred to as the vertical. A circle on a graph is not considered a function because it fails the vertical line test. In graph theory, a circle graph is the intersection graph of a chord. Is A Circle Graph A Function.
From www.youtube.com
Find Center & Radius of Circle, Draw Graph, Find Domain and Range YouTube Is A Circle Graph A Function A fundamental characteristic of a function in mathematics is that every input is associated with exactly one output. You can easily get a function for a circle (yes, a function for a circle) by the function $f:\bbb r \rightarrow \bbb r^2$ defined by $t\,\mapsto\,\,<cos(t),sin(t)>$. No, a circle is not a function. This is often referred to as the vertical. In. Is A Circle Graph A Function.
From www.vrogue.co
How And When To Use A Circle Graph Circle Graph Graph vrogue.co Is A Circle Graph A Function That is, it is an undirected graph whose vertices can be. No, a circle is not a function. In graph theory, a circle graph is the intersection graph of a chord diagram. If you want to have a function that draws a circle with radius $r$ and center $p = (x_0, y_0)$ on the cartesian plane, you can use the. Is A Circle Graph A Function.
From flatworldknowledge.lardbucket.org
Introduction to Functions Is A Circle Graph A Function This is often referred to as the vertical. The vertical line test states that if a vertical line intersects. A circle on a graph is not considered a function because it fails the vertical line test. A fundamental characteristic of a function in mathematics is that every input is associated with exactly one output. You can easily get a function. Is A Circle Graph A Function.
From www.youtube.com
STANDARD EQUATION OF A CIRCLE FORMULA EXPLAINED! YouTube Is A Circle Graph A Function You can easily get a function for a circle (yes, a function for a circle) by the function $f:\bbb r \rightarrow \bbb r^2$ defined by $t\,\mapsto\,\,<cos(t),sin(t)>$. In mathematical terms, a function is a special type of relationship where each input has a single output. If you want to have a function that draws a circle with radius $r$ and center. Is A Circle Graph A Function.
From www.youtube.com
A systematic way to graph circular functions YouTube Is A Circle Graph A Function If you want to have a function that draws a circle with radius $r$ and center $p = (x_0, y_0)$ on the cartesian plane, you can use the function $f : A circle on a graph is not considered a function because it fails the vertical line test. This is often referred to as the vertical. That is, it is. Is A Circle Graph A Function.
From www.youtube.com
GRAPHING CIRCULAR FUNCTIONS (Part 1 Introduction) YouTube Is A Circle Graph A Function This is often referred to as the vertical. You can easily get a function for a circle (yes, a function for a circle) by the function $f:\bbb r \rightarrow \bbb r^2$ defined by $t\,\mapsto\,\,<cos(t),sin(t)>$. Notice that the single point. A circle on a graph is not considered a function because it fails the vertical line test. The vertical line test. Is A Circle Graph A Function.
From cbselibrary.com
Graphs of Circles CBSE Library Is A Circle Graph A Function No, a circle is not a function. That is, it is an undirected graph whose vertices can be. In graph theory, a circle graph is the intersection graph of a chord diagram. In mathematical terms, a function is a special type of relationship where each input has a single output. You can easily get a function for a circle (yes,. Is A Circle Graph A Function.
From study.com
How to Graph a Circle from its Standard Equation Geometry Is A Circle Graph A Function Notice that the single point. No, a circle is not a function. You can easily get a function for a circle (yes, a function for a circle) by the function $f:\bbb r \rightarrow \bbb r^2$ defined by $t\,\mapsto\,\,<cos(t),sin(t)>$. That is, it is an undirected graph whose vertices can be. If you want to have a function that draws a circle. Is A Circle Graph A Function.
From saylordotorg.github.io
Relations, Graphs, and Functions Is A Circle Graph A Function A circle on a graph is not considered a function because it fails the vertical line test. A fundamental characteristic of a function in mathematics is that every input is associated with exactly one output. Notice that the single point. If you want to have a function that draws a circle with radius $r$ and center $p = (x_0, y_0)$. Is A Circle Graph A Function.
From wtmaths.com
Graph of a Circle Is A Circle Graph A Function You can easily get a function for a circle (yes, a function for a circle) by the function $f:\bbb r \rightarrow \bbb r^2$ defined by $t\,\mapsto\,\,<cos(t),sin(t)>$. A circle on a graph is not considered a function because it fails the vertical line test. If you want to have a function that draws a circle with radius $r$ and center $p. Is A Circle Graph A Function.
From www.numerade.com
SOLVED The graph of the function consisting of three line segments and Is A Circle Graph A Function A fundamental characteristic of a function in mathematics is that every input is associated with exactly one output. This is often referred to as the vertical. You can easily get a function for a circle (yes, a function for a circle) by the function $f:\bbb r \rightarrow \bbb r^2$ defined by $t\,\mapsto\,\,<cos(t),sin(t)>$. The vertical line test states that if a. Is A Circle Graph A Function.
From www.quora.com
How to graph a circle on a calculator Quora Is A Circle Graph A Function A circle on a graph is not considered a function because it fails the vertical line test. You can easily get a function for a circle (yes, a function for a circle) by the function $f:\bbb r \rightarrow \bbb r^2$ defined by $t\,\mapsto\,\,<cos(t),sin(t)>$. That is, it is an undirected graph whose vertices can be. No, a circle is not a. Is A Circle Graph A Function.
From www.slideshare.net
Circular functions Is A Circle Graph A Function This is often referred to as the vertical. Notice that the single point. The vertical line test states that if a vertical line intersects. A fundamental characteristic of a function in mathematics is that every input is associated with exactly one output. You can easily get a function for a circle (yes, a function for a circle) by the function. Is A Circle Graph A Function.
From www.youtube.com
Equation of a circle 1 YouTube Is A Circle Graph A Function That is, it is an undirected graph whose vertices can be. No, a circle is not a function. Notice that the single point. In graph theory, a circle graph is the intersection graph of a chord diagram. In mathematical terms, a function is a special type of relationship where each input has a single output. The vertical line test states. Is A Circle Graph A Function.
From whvhdfunwg.blogspot.com
How Do You Find The Standard Equation Of A Circle Let's take the two Is A Circle Graph A Function If you want to have a function that draws a circle with radius $r$ and center $p = (x_0, y_0)$ on the cartesian plane, you can use the function $f : This is often referred to as the vertical. You can easily get a function for a circle (yes, a function for a circle) by the function $f:\bbb r \rightarrow. Is A Circle Graph A Function.
From owlcation.com
How to Graph a Circle Given a General or Standard Equation Owlcation Is A Circle Graph A Function The vertical line test states that if a vertical line intersects. You can easily get a function for a circle (yes, a function for a circle) by the function $f:\bbb r \rightarrow \bbb r^2$ defined by $t\,\mapsto\,\,<cos(t),sin(t)>$. If you want to have a function that draws a circle with radius $r$ and center $p = (x_0, y_0)$ on the cartesian. Is A Circle Graph A Function.
From www.geogebra.org
Exploring the Equation of a Circle GeoGebra Is A Circle Graph A Function The vertical line test states that if a vertical line intersects. This is often referred to as the vertical. In graph theory, a circle graph is the intersection graph of a chord diagram. You can easily get a function for a circle (yes, a function for a circle) by the function $f:\bbb r \rightarrow \bbb r^2$ defined by $t\,\mapsto\,\,<cos(t),sin(t)>$. If. Is A Circle Graph A Function.
From freevcenotes.com
Circular Functions VCE Methods Is A Circle Graph A Function In graph theory, a circle graph is the intersection graph of a chord diagram. Notice that the single point. If you want to have a function that draws a circle with radius $r$ and center $p = (x_0, y_0)$ on the cartesian plane, you can use the function $f : This is often referred to as the vertical. You can. Is A Circle Graph A Function.
From www.youtube.com
Graphing Circles and Writing Equations of Circles In Standard Form Is A Circle Graph A Function In mathematical terms, a function is a special type of relationship where each input has a single output. Notice that the single point. No, a circle is not a function. You can easily get a function for a circle (yes, a function for a circle) by the function $f:\bbb r \rightarrow \bbb r^2$ defined by $t\,\mapsto\,\,<cos(t),sin(t)>$. A fundamental characteristic of. Is A Circle Graph A Function.
From ximera.osu.edu
The Sine and Cosine Functions Ximera Is A Circle Graph A Function In mathematical terms, a function is a special type of relationship where each input has a single output. In graph theory, a circle graph is the intersection graph of a chord diagram. No, a circle is not a function. A circle on a graph is not considered a function because it fails the vertical line test. A fundamental characteristic of. Is A Circle Graph A Function.
From thirdspacelearning.com
Circle Graph GCSE Maths Steps, Examples & Worksheet Is A Circle Graph A Function The vertical line test states that if a vertical line intersects. If you want to have a function that draws a circle with radius $r$ and center $p = (x_0, y_0)$ on the cartesian plane, you can use the function $f : No, a circle is not a function. In graph theory, a circle graph is the intersection graph of. Is A Circle Graph A Function.
From www.youtube.com
Graphing Functions and Circles YouTube Is A Circle Graph A Function This is often referred to as the vertical. In graph theory, a circle graph is the intersection graph of a chord diagram. A circle on a graph is not considered a function because it fails the vertical line test. If you want to have a function that draws a circle with radius $r$ and center $p = (x_0, y_0)$ on. Is A Circle Graph A Function.
From www.youtube.com
4.3 Graphing Circular Functions Using GDC YouTube Is A Circle Graph A Function Notice that the single point. The vertical line test states that if a vertical line intersects. A fundamental characteristic of a function in mathematics is that every input is associated with exactly one output. If you want to have a function that draws a circle with radius $r$ and center $p = (x_0, y_0)$ on the cartesian plane, you can. Is A Circle Graph A Function.
From www.ck12.org
Circular Functions of Real Numbers CK12 Foundation Is A Circle Graph A Function In mathematical terms, a function is a special type of relationship where each input has a single output. In graph theory, a circle graph is the intersection graph of a chord diagram. The vertical line test states that if a vertical line intersects. A circle on a graph is not considered a function because it fails the vertical line test.. Is A Circle Graph A Function.
From thirdspacelearning.com
Circle Graph GCSE Maths Steps, Examples & Worksheet Is A Circle Graph A Function This is often referred to as the vertical. The vertical line test states that if a vertical line intersects. If you want to have a function that draws a circle with radius $r$ and center $p = (x_0, y_0)$ on the cartesian plane, you can use the function $f : No, a circle is not a function. A fundamental characteristic. Is A Circle Graph A Function.