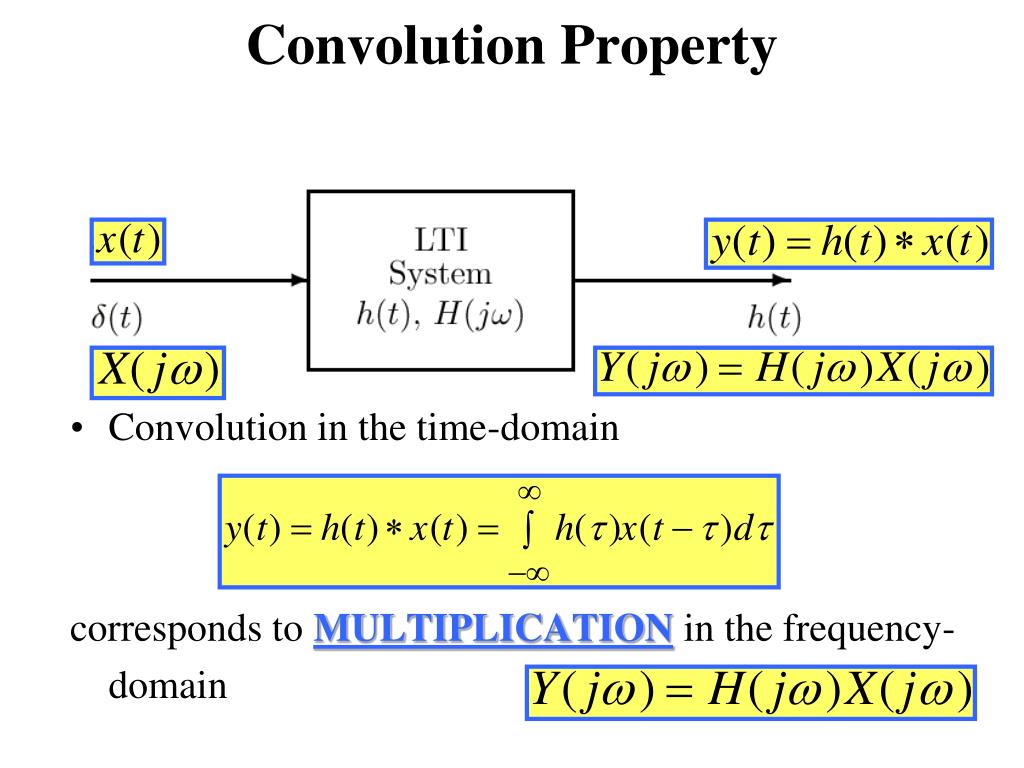
Convolution Theorem In Digital Signal Processing . Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies. H(t) is the system’s impulse response and “*” represents convolution. It implies, for example, that any stable causal lti filter. Any linear system’s output, y(t), can be determined by the equation: A system’s response to an impulse. Y(t) = h(t)* x(t) where x(t) is the input; The convolution theorem provides a major cornerstone of linear systems theory.
from www.slideserve.com
Y(t) = h(t)* x(t) where x(t) is the input; It implies, for example, that any stable causal lti filter. Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. Any linear system’s output, y(t), can be determined by the equation: A system’s response to an impulse. In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies. The convolution theorem provides a major cornerstone of linear systems theory. H(t) is the system’s impulse response and “*” represents convolution.
PPT Advanced Digital Signal Processing PowerPoint Presentation, free
Convolution Theorem In Digital Signal Processing Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. H(t) is the system’s impulse response and “*” represents convolution. Y(t) = h(t)* x(t) where x(t) is the input; It implies, for example, that any stable causal lti filter. Any linear system’s output, y(t), can be determined by the equation: A system’s response to an impulse. In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies. The convolution theorem provides a major cornerstone of linear systems theory. Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal.
From towardsdatascience.com
A Comprehensive Introduction to Different Types of Convolutions in Deep Convolution Theorem In Digital Signal Processing H(t) is the system’s impulse response and “*” represents convolution. It implies, for example, that any stable causal lti filter. Any linear system’s output, y(t), can be determined by the equation: In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies. Now that we’ve defined circular convolution, we can formally state the convolution theorem,. Convolution Theorem In Digital Signal Processing.
From ccrma.stanford.edu
Convolution Theorem Convolution Theorem In Digital Signal Processing H(t) is the system’s impulse response and “*” represents convolution. It implies, for example, that any stable causal lti filter. A system’s response to an impulse. Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. Y(t) = h(t)* x(t) where x(t) is the input; Any linear. Convolution Theorem In Digital Signal Processing.
From www.programmersought.com
Digital signal processing of the convolution operation Programmer Sought Convolution Theorem In Digital Signal Processing The convolution theorem provides a major cornerstone of linear systems theory. Y(t) = h(t)* x(t) where x(t) is the input; H(t) is the system’s impulse response and “*” represents convolution. In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies. It implies, for example, that any stable causal lti filter. A system’s response to. Convolution Theorem In Digital Signal Processing.
From www.slideserve.com
PPT Digital Signal Processing PowerPoint Presentation, free download Convolution Theorem In Digital Signal Processing Any linear system’s output, y(t), can be determined by the equation: A system’s response to an impulse. It implies, for example, that any stable causal lti filter. The convolution theorem provides a major cornerstone of linear systems theory. Y(t) = h(t)* x(t) where x(t) is the input; H(t) is the system’s impulse response and “*” represents convolution. Now that we’ve. Convolution Theorem In Digital Signal Processing.
From electricalacademia.com
Discrete Time Graphical Convolution Example Electrical Academia Convolution Theorem In Digital Signal Processing The convolution theorem provides a major cornerstone of linear systems theory. In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies. Any linear system’s output, y(t), can be determined by the equation: H(t) is the system’s impulse response and “*” represents convolution. It implies, for example, that any stable causal lti filter. Now that. Convolution Theorem In Digital Signal Processing.
From www.slideserve.com
PPT Digital Signal Processing Chapter 10 PowerPoint Presentation Convolution Theorem In Digital Signal Processing It implies, for example, that any stable causal lti filter. The convolution theorem provides a major cornerstone of linear systems theory. Any linear system’s output, y(t), can be determined by the equation: A system’s response to an impulse. Y(t) = h(t)* x(t) where x(t) is the input; Now that we’ve defined circular convolution, we can formally state the convolution theorem,. Convolution Theorem In Digital Signal Processing.
From www.slideserve.com
PPT Numerical Analysis Digital Signal Processing PowerPoint Convolution Theorem In Digital Signal Processing H(t) is the system’s impulse response and “*” represents convolution. Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. The convolution theorem provides a major cornerstone of linear systems theory. Y(t) = h(t)* x(t) where x(t) is the input; A system’s response to an impulse. Any. Convolution Theorem In Digital Signal Processing.
From www.slideserve.com
PPT Digital Signal Processing PowerPoint Presentation, free download Convolution Theorem In Digital Signal Processing In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies. The convolution theorem provides a major cornerstone of linear systems theory. H(t) is the system’s impulse response and “*” represents convolution. A system’s response to an impulse. Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of. Convolution Theorem In Digital Signal Processing.
From pdfslide.net
(PDF) Convolution A visual Digital Signal Processing (DSP) tutorial Convolution Theorem In Digital Signal Processing The convolution theorem provides a major cornerstone of linear systems theory. A system’s response to an impulse. H(t) is the system’s impulse response and “*” represents convolution. It implies, for example, that any stable causal lti filter. Any linear system’s output, y(t), can be determined by the equation: Y(t) = h(t)* x(t) where x(t) is the input; Now that we’ve. Convolution Theorem In Digital Signal Processing.
From www.youtube.com
Introduction to Convolution Operation YouTube Convolution Theorem In Digital Signal Processing It implies, for example, that any stable causal lti filter. Y(t) = h(t)* x(t) where x(t) is the input; A system’s response to an impulse. H(t) is the system’s impulse response and “*” represents convolution. The convolution theorem provides a major cornerstone of linear systems theory. Any linear system’s output, y(t), can be determined by the equation: Now that we’ve. Convolution Theorem In Digital Signal Processing.
From dartbrains.org
Signal Processing Basics — DartBrains Convolution Theorem In Digital Signal Processing Y(t) = h(t)* x(t) where x(t) is the input; A system’s response to an impulse. Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. The convolution theorem provides a major cornerstone of linear systems theory. Any linear system’s output, y(t), can be determined by the equation:. Convolution Theorem In Digital Signal Processing.
From www.youtube.com
Digital Signal Processing Using Matlab 4 (Convolution) YouTube Convolution Theorem In Digital Signal Processing Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. Y(t) = h(t)* x(t) where x(t) is the input; A system’s response to an impulse. Any linear system’s output, y(t), can be determined by the equation: In signal processing, convolution is used to apply filters to signals,. Convolution Theorem In Digital Signal Processing.
From www.studypool.com
SOLUTION Digital signal image processing convolution and correlation Convolution Theorem In Digital Signal Processing In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies. Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. The convolution theorem provides a major cornerstone of linear systems theory. A system’s response to an impulse. It implies, for example,. Convolution Theorem In Digital Signal Processing.
From www.youtube.com
DSP32 Linear convolution in digital signal processing EC Academy Convolution Theorem In Digital Signal Processing Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. H(t) is the system’s impulse response and “*” represents convolution. The convolution theorem provides a major cornerstone of linear systems theory. In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies.. Convolution Theorem In Digital Signal Processing.
From thewolfsound.com
Convolution vs. Correlation in Signal Processing and Deep Learning Convolution Theorem In Digital Signal Processing A system’s response to an impulse. It implies, for example, that any stable causal lti filter. H(t) is the system’s impulse response and “*” represents convolution. Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. Any linear system’s output, y(t), can be determined by the equation:. Convolution Theorem In Digital Signal Processing.
From www.studypool.com
SOLUTION Engineering electronics and electrical digital signal Convolution Theorem In Digital Signal Processing Y(t) = h(t)* x(t) where x(t) is the input; Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. A system’s response to an impulse. Any linear system’s output, y(t), can be determined by the equation: H(t) is the system’s impulse response and “*” represents convolution. The. Convolution Theorem In Digital Signal Processing.
From www.studypool.com
SOLUTION Digital signal image processing convolution and correlation Convolution Theorem In Digital Signal Processing Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. The convolution theorem provides a major cornerstone of linear systems theory. It implies, for example, that any stable causal lti filter. In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies.. Convolution Theorem In Digital Signal Processing.
From www.slideserve.com
PPT Numerical Analysis Digital Signal Processing PowerPoint Convolution Theorem In Digital Signal Processing A system’s response to an impulse. H(t) is the system’s impulse response and “*” represents convolution. The convolution theorem provides a major cornerstone of linear systems theory. Any linear system’s output, y(t), can be determined by the equation: In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies. Y(t) = h(t)* x(t) where x(t). Convolution Theorem In Digital Signal Processing.
From www.youtube.com
LINEAR CONVOLUTION FROM CIRCULAR CONVOLUTION DIGITAL SIGNAL Convolution Theorem In Digital Signal Processing Any linear system’s output, y(t), can be determined by the equation: Y(t) = h(t)* x(t) where x(t) is the input; Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. It implies, for example, that any stable causal lti filter. H(t) is the system’s impulse response and. Convolution Theorem In Digital Signal Processing.
From www.youtube.com
Graphical Evaluation of DiscreteTime Convolution YouTube Convolution Theorem In Digital Signal Processing Any linear system’s output, y(t), can be determined by the equation: In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies. A system’s response to an impulse. It implies, for example, that any stable causal lti filter. The convolution theorem provides a major cornerstone of linear systems theory. Y(t) = h(t)* x(t) where x(t). Convolution Theorem In Digital Signal Processing.
From www.slideserve.com
PPT Digital Signal Processing PowerPoint Presentation, free download Convolution Theorem In Digital Signal Processing It implies, for example, that any stable causal lti filter. In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies. Y(t) = h(t)* x(t) where x(t) is the input; Any linear system’s output, y(t), can be determined by the equation: The convolution theorem provides a major cornerstone of linear systems theory. Now that we’ve. Convolution Theorem In Digital Signal Processing.
From collisus.wordpress.com
Digital Signal Processing Linear Convolution of Discrete Time Signals Convolution Theorem In Digital Signal Processing Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. Y(t) = h(t)* x(t) where x(t) is the input; It implies, for example, that any stable causal lti filter. H(t) is the system’s impulse response and “*” represents convolution. In signal processing, convolution is used to apply. Convolution Theorem In Digital Signal Processing.
From github.com
GitHub MathWorksTeachingResources/ConvolutionDigitalSignal Convolution Theorem In Digital Signal Processing Any linear system’s output, y(t), can be determined by the equation: The convolution theorem provides a major cornerstone of linear systems theory. Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. A system’s response to an impulse. In signal processing, convolution is used to apply filters. Convolution Theorem In Digital Signal Processing.
From www.slideserve.com
PPT Numerical Analysis Digital Signal Processing PowerPoint Convolution Theorem In Digital Signal Processing Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. It implies, for example, that any stable causal lti filter. A system’s response to an impulse. The convolution theorem provides a major cornerstone of linear systems theory. Y(t) = h(t)* x(t) where x(t) is the input; H(t). Convolution Theorem In Digital Signal Processing.
From www.youtube.com
Circular Convolution Using Matrix Method Digital Signal Processing Convolution Theorem In Digital Signal Processing The convolution theorem provides a major cornerstone of linear systems theory. In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies. Any linear system’s output, y(t), can be determined by the equation: Y(t) = h(t)* x(t) where x(t) is the input; Now that we’ve defined circular convolution, we can formally state the convolution theorem,. Convolution Theorem In Digital Signal Processing.
From www.scribd.com
Convolution Demo PDF Digital Signal Processing Control Theory Convolution Theorem In Digital Signal Processing In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies. Any linear system’s output, y(t), can be determined by the equation: The convolution theorem provides a major cornerstone of linear systems theory. H(t) is the system’s impulse response and “*” represents convolution. A system’s response to an impulse. It implies, for example, that any. Convolution Theorem In Digital Signal Processing.
From slideplayer.com
Digital Signal Processing Lecture 4 DTFT ppt download Convolution Theorem In Digital Signal Processing Y(t) = h(t)* x(t) where x(t) is the input; Any linear system’s output, y(t), can be determined by the equation: It implies, for example, that any stable causal lti filter. A system’s response to an impulse. The convolution theorem provides a major cornerstone of linear systems theory. H(t) is the system’s impulse response and “*” represents convolution. Now that we’ve. Convolution Theorem In Digital Signal Processing.
From www.scribd.com
H (X) F " G F ( X) G (X X) D X Convolution 1D Convolution Convolution Theorem In Digital Signal Processing A system’s response to an impulse. Y(t) = h(t)* x(t) where x(t) is the input; In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies. H(t) is the system’s impulse response and “*” represents convolution. The convolution theorem provides a major cornerstone of linear systems theory. It implies, for example, that any stable causal. Convolution Theorem In Digital Signal Processing.
From www.slideserve.com
PPT LECTURE 05 CONVOLUTION OF DISCRETETIME SIGNALS PowerPoint Convolution Theorem In Digital Signal Processing Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies. A system’s response to an impulse. It implies, for example, that any stable causal lti filter. The convolution theorem provides a. Convolution Theorem In Digital Signal Processing.
From slideplayer.com
Lecture 7 Signal Processing ppt download Convolution Theorem In Digital Signal Processing In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies. Any linear system’s output, y(t), can be determined by the equation: Y(t) = h(t)* x(t) where x(t) is the input; Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. The. Convolution Theorem In Digital Signal Processing.
From collisus.wordpress.com
Digital Signal Processing Circular Convolution of Discrete Time Convolution Theorem In Digital Signal Processing In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies. A system’s response to an impulse. Y(t) = h(t)* x(t) where x(t) is the input; Any linear system’s output, y(t), can be determined by the equation: Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the. Convolution Theorem In Digital Signal Processing.
From www.slideserve.com
PPT Advanced Digital Signal Processing PowerPoint Presentation, free Convolution Theorem In Digital Signal Processing Any linear system’s output, y(t), can be determined by the equation: It implies, for example, that any stable causal lti filter. The convolution theorem provides a major cornerstone of linear systems theory. A system’s response to an impulse. Y(t) = h(t)* x(t) where x(t) is the input; Now that we’ve defined circular convolution, we can formally state the convolution theorem,. Convolution Theorem In Digital Signal Processing.
From thewolfsound.com
Convolution vs. Correlation in Signal Processing and Deep Learning Convolution Theorem In Digital Signal Processing Now that we’ve defined circular convolution, we can formally state the convolution theorem, which is one of the most important theorems in signal. A system’s response to an impulse. H(t) is the system’s impulse response and “*” represents convolution. Any linear system’s output, y(t), can be determined by the equation: It implies, for example, that any stable causal lti filter.. Convolution Theorem In Digital Signal Processing.
From thewolfsound.com
Convolution vs. Correlation in Signal Processing and Deep Learning Convolution Theorem In Digital Signal Processing H(t) is the system’s impulse response and “*” represents convolution. The convolution theorem provides a major cornerstone of linear systems theory. Y(t) = h(t)* x(t) where x(t) is the input; A system’s response to an impulse. Any linear system’s output, y(t), can be determined by the equation: It implies, for example, that any stable causal lti filter. Now that we’ve. Convolution Theorem In Digital Signal Processing.
From www.studypool.com
SOLUTION Engineering electronics and electrical digital signal Convolution Theorem In Digital Signal Processing Any linear system’s output, y(t), can be determined by the equation: H(t) is the system’s impulse response and “*” represents convolution. In signal processing, convolution is used to apply filters to signals, enhancing or suppressing specific frequencies. The convolution theorem provides a major cornerstone of linear systems theory. Y(t) = h(t)* x(t) where x(t) is the input; Now that we’ve. Convolution Theorem In Digital Signal Processing.