Harmonic Oscillator Frequency . The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the stiffness of the restoring force and the.
from studylib.net
Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the stiffness of the restoring force and the. (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get.
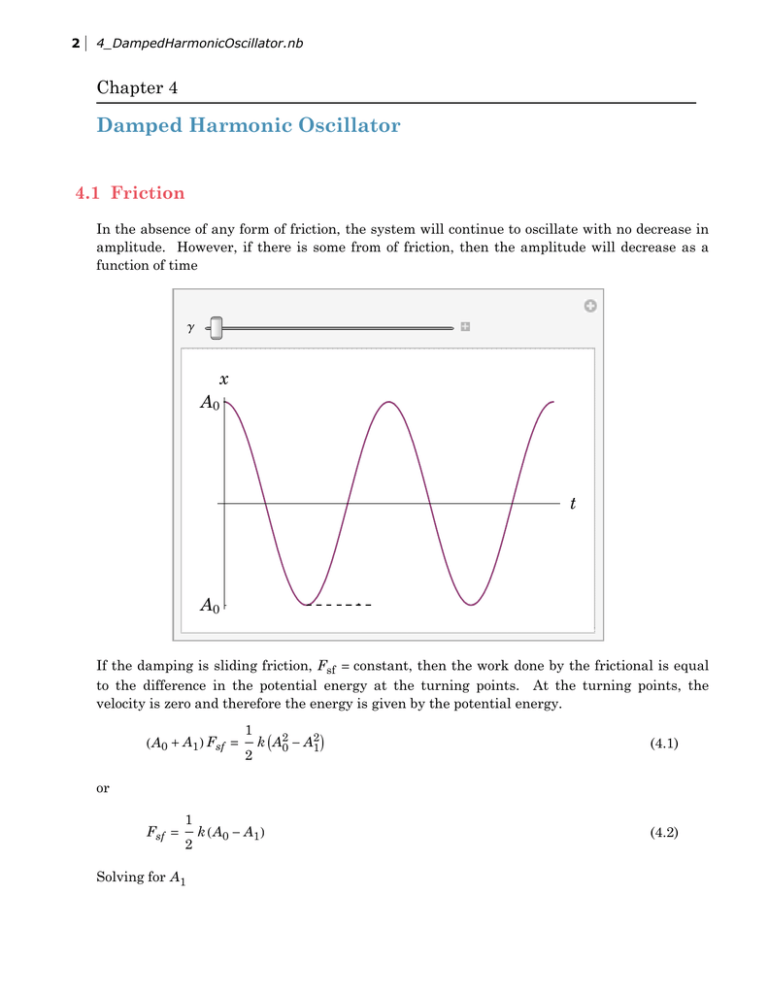
Damped Harmonic Oscillator
Harmonic Oscillator Frequency Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the stiffness of the restoring force and the. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the stiffness of the restoring force and the. (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the.
From tikz.net
Harmonic oscillator plots Harmonic Oscillator Frequency One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the stiffness of the restoring force and the. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of. Harmonic Oscillator Frequency.
From www.researchgate.net
We consider the harmonic oscillator with time dependent frequency ω t Harmonic Oscillator Frequency Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the stiffness of the restoring force and the. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get. One of the. Harmonic Oscillator Frequency.
From www.slideserve.com
PPT Chemistry 2 PowerPoint Presentation, free download ID3158071 Harmonic Oscillator Frequency One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the. Harmonic Oscillator Frequency.
From www.slideserve.com
PPT Unit 6 Lesson 1 Simple Harmonic Motion SHM PowerPoint Harmonic Oscillator Frequency Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the stiffness of the restoring force and the. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get. One of the. Harmonic Oscillator Frequency.
From www.youtube.com
Harmonic oscillator energy levels difference derivation YouTube Harmonic Oscillator Frequency The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Simple harmonic motion evolves over time like. Harmonic Oscillator Frequency.
From tikz.net
Harmonic Oscillator Energy vs. Angular Frequency Harmonic Oscillator Frequency One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for. Harmonic Oscillator Frequency.
From www.youtube.com
Dynamics Lecture Simple Harmonic Oscillator,MassSpring, Natural Harmonic Oscillator Frequency (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the. Harmonic Oscillator Frequency.
From en.ppt-online.org
Oscillatory motion. Simple harmonic motion. The simple pendulum. Damped Harmonic Oscillator Frequency The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get. (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. Simple harmonic motion evolves over time like. Harmonic Oscillator Frequency.
From animalia-life.club
Damped Harmonic Oscillator Examples Harmonic Oscillator Frequency (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the. Harmonic Oscillator Frequency.
From www.slideserve.com
PPT Simple Harmonic Motion PowerPoint Presentation, free download Harmonic Oscillator Frequency (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get. One of the most important examples of. Harmonic Oscillator Frequency.
From owlcation.com
Solution of Schrödinger Equation for Simple Harmonic Oscillator Owlcation Harmonic Oscillator Frequency (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get. Simple harmonic motion evolves over time like. Harmonic Oscillator Frequency.
From www.slideserve.com
PPT Waves Oscillations PowerPoint Presentation, free download ID Harmonic Oscillator Frequency One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the. Harmonic Oscillator Frequency.
From www.slideserve.com
PPT PHYSICS 231 Lecture 33 Oscillations PowerPoint Presentation Harmonic Oscillator Frequency (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get. Simple harmonic motion evolves over time like. Harmonic Oscillator Frequency.
From www.numerade.com
SOLVED If the spring constant of simple harmonic oscillator halved, bY Harmonic Oscillator Frequency Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the stiffness of the restoring force and the. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of. Harmonic Oscillator Frequency.
From en.ppt-online.org
Oscillatory motion. Simple harmonic motion. The simple pendulum. Damped Harmonic Oscillator Frequency (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the. Harmonic Oscillator Frequency.
From www.youtube.com
The Quantum Harmonic Oscillator Part 1 The Classical Harmonic Harmonic Oscillator Frequency Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the stiffness of the restoring force and the. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get. One of the. Harmonic Oscillator Frequency.
From courses.lumenlearning.com
Energy and the Simple Harmonic Oscillator Physics Harmonic Oscillator Frequency The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get. Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the stiffness of the restoring force and the. (we will call. Harmonic Oscillator Frequency.
From mminsight.com
Simple harmonic oscillator (မိတ်ဆက် ၂) Insight for Myanmar Harmonic Oscillator Frequency One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get. (we will call $\omega_0$ the natural frequency. Harmonic Oscillator Frequency.
From www.youtube.com
Simple Harmonic Motion (15 of 16) Amplitude, Period & Frequency YouTube Harmonic Oscillator Frequency (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the stiffness of the restoring force and the. One of the most important examples of periodic motion is simple harmonic motion (shm),. Harmonic Oscillator Frequency.
From www.slideserve.com
PPT Lecture D31 Linear Harmonic Oscillator PowerPoint Presentation Harmonic Oscillator Frequency (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get. One of the most important examples of. Harmonic Oscillator Frequency.
From www.youtube.com
Energy in Simple Harmonic Oscillators YouTube Harmonic Oscillator Frequency (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for. Harmonic Oscillator Frequency.
From www.youtube.com
Beats Superposition of two simple harmonic oscillations of different Harmonic Oscillator Frequency One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the stiffness of the restoring force and the. (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the. Harmonic Oscillator Frequency.
From www.youtube.com
Introduction to the Quantum Harmonic Oscillator Wavefunction? Energy Harmonic Oscillator Frequency (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the. Harmonic Oscillator Frequency.
From www.slideserve.com
PPT 5. The Harmonic Oscillator PowerPoint Presentation, free download Harmonic Oscillator Frequency The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get. Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the stiffness of the restoring force and the. (we will call. Harmonic Oscillator Frequency.
From www.researchgate.net
(a) Schematic representation of a harmonic oscillator ({ \mathcal S Harmonic Oscillator Frequency (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for. Harmonic Oscillator Frequency.
From byjus.com
A light damped oscillator with the frequency (ω) is set in motion by Harmonic Oscillator Frequency (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for. Harmonic Oscillator Frequency.
From www.slideserve.com
PPT Light (EM Radiation) Characteristics PowerPoint Presentation Harmonic Oscillator Frequency The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. (we will call $\omega_0$ the natural frequency. Harmonic Oscillator Frequency.
From www.researchgate.net
Phase portraits of harmonic oscillator pairs with different frequency Harmonic Oscillator Frequency The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Simple harmonic motion evolves over time like. Harmonic Oscillator Frequency.
From studylib.net
Damped Harmonic Oscillator Harmonic Oscillator Frequency One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for. Harmonic Oscillator Frequency.
From www.youtube.com
Simple Harmonic Motion Period and Frequency YouTube Harmonic Oscillator Frequency The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. (we will call $\omega_0$ the natural frequency. Harmonic Oscillator Frequency.
From www.studypool.com
SOLUTION Factors Affecting The Frequency Of A Simple Harmonic Harmonic Oscillator Frequency The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for the phase to change by one complete cycle, or \(2π\) radians, and thus get. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. Simple harmonic motion evolves over time like. Harmonic Oscillator Frequency.
From www.researchgate.net
Frequency response of the harmonic oscillator amplitude (top) and Harmonic Oscillator Frequency (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the stiffness of the restoring force and the. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of. Harmonic Oscillator Frequency.
From www.slideserve.com
PPT Quantum Harmonic Oscillator PowerPoint Presentation, free Harmonic Oscillator Frequency (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of the time required for. Harmonic Oscillator Frequency.
From universe-review.ca
Harmonic Oscillator Harmonic Oscillator Frequency (we will call $\omega_0$ the natural frequency of the harmonic oscillator, and $\omega$ the applied frequency.) at very high frequency the. Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the stiffness of the restoring force and the. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of. Harmonic Oscillator Frequency.
From www.doubtnut.com
The velocitytime diagram of a harmonic oscillator is shown in the adj Harmonic Oscillator Frequency Simple harmonic motion evolves over time like a sine function with a frequency that depends only upon the stiffness of the restoring force and the. One of the most important examples of periodic motion is simple harmonic motion (shm), in which some physical quantity varies sinusoidally. The “frequency”, usually denoted by the greek letter, \(ν\) (nu), is the inverse of. Harmonic Oscillator Frequency.