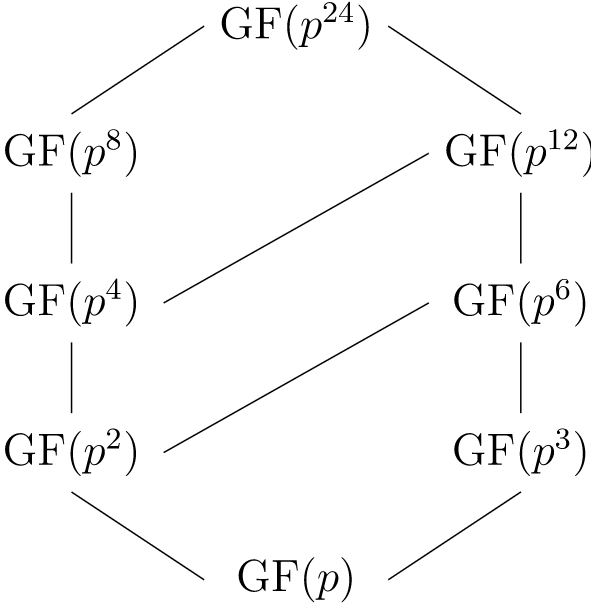
Finite Field Extension Cyclic . in this paper we prove the decidability of the theory of finite fields and. i have found proving the key theorem that finite multiplicative subgroups of fields are cyclic a pedagogical speedbump. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. any finite extension of a finite field $\mathbb{f}_q$ is cyclic. if an extension field \(e\) of a field \(f\) is a finite dimensional vector space over \(f\) of dimension \(n\text{,}\) then we say that. If is a generator, then every nonzero element of f is a power of. we note that the multiplicative group (f;) is cyclic. For such an extension $k$ first recall that the. let $ \mathbb{k} $ be a field and $ \mathbb{f} $ a subfield.
from math.libretexts.org
i have found proving the key theorem that finite multiplicative subgroups of fields are cyclic a pedagogical speedbump. in this paper we prove the decidability of the theory of finite fields and. let $ \mathbb{k} $ be a field and $ \mathbb{f} $ a subfield. if an extension field \(e\) of a field \(f\) is a finite dimensional vector space over \(f\) of dimension \(n\text{,}\) then we say that. we note that the multiplicative group (f;) is cyclic. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. any finite extension of a finite field $\mathbb{f}_q$ is cyclic. For such an extension $k$ first recall that the. If is a generator, then every nonzero element of f is a power of.
22.1 Structure of a Finite Field Mathematics LibreTexts
Finite Field Extension Cyclic i have found proving the key theorem that finite multiplicative subgroups of fields are cyclic a pedagogical speedbump. any finite extension of a finite field $\mathbb{f}_q$ is cyclic. For such an extension $k$ first recall that the. i have found proving the key theorem that finite multiplicative subgroups of fields are cyclic a pedagogical speedbump. in this paper we prove the decidability of the theory of finite fields and. we note that the multiplicative group (f;) is cyclic. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. If is a generator, then every nonzero element of f is a power of. let $ \mathbb{k} $ be a field and $ \mathbb{f} $ a subfield. if an extension field \(e\) of a field \(f\) is a finite dimensional vector space over \(f\) of dimension \(n\text{,}\) then we say that.
From www.youtube.com
Algebraic Field Extensions, Finite Degree Extensions, Multiplicative Property of Field Finite Field Extension Cyclic let $ \mathbb{k} $ be a field and $ \mathbb{f} $ a subfield. For such an extension $k$ first recall that the. If is a generator, then every nonzero element of f is a power of. we note that the multiplicative group (f;) is cyclic. i have found proving the key theorem that finite multiplicative subgroups of. Finite Field Extension Cyclic.
From www.chegg.com
Solved Let E be an extension field of a finite field F, Finite Field Extension Cyclic we note that the multiplicative group (f;) is cyclic. If is a generator, then every nonzero element of f is a power of. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. let $ \mathbb{k} $ be a field and $ \mathbb{f} $ a subfield. i have found proving the key theorem that finite multiplicative subgroups. Finite Field Extension Cyclic.
From www.slideserve.com
PPT Cyclic Codes PowerPoint Presentation, free download ID314590 Finite Field Extension Cyclic in this paper we prove the decidability of the theory of finite fields and. if an extension field \(e\) of a field \(f\) is a finite dimensional vector space over \(f\) of dimension \(n\text{,}\) then we say that. let $ \mathbb{k} $ be a field and $ \mathbb{f} $ a subfield. We say that $ \mathbb{k}/\mathbb{f} $. Finite Field Extension Cyclic.
From www.youtube.com
Complex and Algebraic Numbers, Finite Field Extensions YouTube Finite Field Extension Cyclic For such an extension $k$ first recall that the. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. any finite extension of a finite field $\mathbb{f}_q$ is cyclic. if an extension field \(e\) of a field \(f\) is a finite dimensional vector space over \(f\) of dimension \(n\text{,}\) then we say that. let $ \mathbb{k} $. Finite Field Extension Cyclic.
From www.researchgate.net
(PDF) Normal high order elements in finite field extensions based on the cyclotomic polynomials Finite Field Extension Cyclic any finite extension of a finite field $\mathbb{f}_q$ is cyclic. If is a generator, then every nonzero element of f is a power of. if an extension field \(e\) of a field \(f\) is a finite dimensional vector space over \(f\) of dimension \(n\text{,}\) then we say that. we note that the multiplicative group (f;) is cyclic.. Finite Field Extension Cyclic.
From www.researchgate.net
(PDF) PRIMITIVE ELEMENT PAIRS WITH A PRESCRIBED TRACE IN THE CUBIC EXTENSION OF A FINITE FIELD Finite Field Extension Cyclic We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. any finite extension of a finite field $\mathbb{f}_q$ is cyclic. If is a generator, then every nonzero element of f is a power of. if an extension field \(e\) of a field \(f\) is a finite dimensional vector space over \(f\) of dimension \(n\text{,}\) then we say that.. Finite Field Extension Cyclic.
From www.slideserve.com
PPT Chapter 4 Finite Fields PowerPoint Presentation, free download ID5466031 Finite Field Extension Cyclic we note that the multiplicative group (f;) is cyclic. let $ \mathbb{k} $ be a field and $ \mathbb{f} $ a subfield. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. If is a generator, then every nonzero element of f is a power of. if an extension field \(e\) of a field \(f\) is a. Finite Field Extension Cyclic.
From www.youtube.com
Fields examples Finite field YouTube Finite Field Extension Cyclic i have found proving the key theorem that finite multiplicative subgroups of fields are cyclic a pedagogical speedbump. we note that the multiplicative group (f;) is cyclic. in this paper we prove the decidability of the theory of finite fields and. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. If is a generator, then every. Finite Field Extension Cyclic.
From www.youtube.com
Theorem Finite extension of a finite extension is also finite extension [LF] = [LK] [KF Finite Field Extension Cyclic i have found proving the key theorem that finite multiplicative subgroups of fields are cyclic a pedagogical speedbump. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. If is a generator, then every nonzero element of f is a power of. let $ \mathbb{k} $ be a field and $ \mathbb{f} $ a subfield. if an. Finite Field Extension Cyclic.
From www.youtube.com
Abstr Alg, 35B Classification of Finite Fields, Finite Extensions, and Algebraic Field Finite Field Extension Cyclic any finite extension of a finite field $\mathbb{f}_q$ is cyclic. For such an extension $k$ first recall that the. If is a generator, then every nonzero element of f is a power of. let $ \mathbb{k} $ be a field and $ \mathbb{f} $ a subfield. if an extension field \(e\) of a field \(f\) is a. Finite Field Extension Cyclic.
From www.slideserve.com
PPT Cyclic Codes PowerPoint Presentation, free download ID314590 Finite Field Extension Cyclic let $ \mathbb{k} $ be a field and $ \mathbb{f} $ a subfield. If is a generator, then every nonzero element of f is a power of. any finite extension of a finite field $\mathbb{f}_q$ is cyclic. we note that the multiplicative group (f;) is cyclic. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. . Finite Field Extension Cyclic.
From www.youtube.com
Theorem Every finite extension is an algebraic Extension Field Theory Abstract Algebra Finite Field Extension Cyclic For such an extension $k$ first recall that the. any finite extension of a finite field $\mathbb{f}_q$ is cyclic. in this paper we prove the decidability of the theory of finite fields and. if an extension field \(e\) of a field \(f\) is a finite dimensional vector space over \(f\) of dimension \(n\text{,}\) then we say that.. Finite Field Extension Cyclic.
From www.youtube.com
Structure of Finite Fields YouTube Finite Field Extension Cyclic let $ \mathbb{k} $ be a field and $ \mathbb{f} $ a subfield. if an extension field \(e\) of a field \(f\) is a finite dimensional vector space over \(f\) of dimension \(n\text{,}\) then we say that. any finite extension of a finite field $\mathbb{f}_q$ is cyclic. i have found proving the key theorem that finite. Finite Field Extension Cyclic.
From www.slideserve.com
PPT Cyclic Codes PowerPoint Presentation, free download ID314590 Finite Field Extension Cyclic For such an extension $k$ first recall that the. in this paper we prove the decidability of the theory of finite fields and. any finite extension of a finite field $\mathbb{f}_q$ is cyclic. if an extension field \(e\) of a field \(f\) is a finite dimensional vector space over \(f\) of dimension \(n\text{,}\) then we say that.. Finite Field Extension Cyclic.
From www.chegg.com
Solved C. Finite Extensions of Finite Fields By the proof of Finite Field Extension Cyclic For such an extension $k$ first recall that the. we note that the multiplicative group (f;) is cyclic. If is a generator, then every nonzero element of f is a power of. if an extension field \(e\) of a field \(f\) is a finite dimensional vector space over \(f\) of dimension \(n\text{,}\) then we say that. any. Finite Field Extension Cyclic.
From www.semanticscholar.org
Figure 2 from FINITE FIELDS AND DECODING OF CYCLC CODES Semantic Scholar Finite Field Extension Cyclic if an extension field \(e\) of a field \(f\) is a finite dimensional vector space over \(f\) of dimension \(n\text{,}\) then we say that. i have found proving the key theorem that finite multiplicative subgroups of fields are cyclic a pedagogical speedbump. For such an extension $k$ first recall that the. in this paper we prove the. Finite Field Extension Cyclic.
From www.slideserve.com
PPT SECTION 6 Cyclic Groups PowerPoint Presentation, free download ID3091707 Finite Field Extension Cyclic For such an extension $k$ first recall that the. If is a generator, then every nonzero element of f is a power of. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. i have found proving the key theorem that finite multiplicative subgroups of fields are cyclic a pedagogical speedbump. we note that the multiplicative group (f;). Finite Field Extension Cyclic.
From www.chegg.com
Solved 3. (a) (8 marks) Define i. A finite field extension. Finite Field Extension Cyclic we note that the multiplicative group (f;) is cyclic. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. any finite extension of a finite field $\mathbb{f}_q$ is cyclic. If is a generator, then every nonzero element of f is a power of. i have found proving the key theorem that finite multiplicative subgroups of fields are. Finite Field Extension Cyclic.
From www.researchgate.net
(PDF) Reliable Architectures for Finite Field Multipliers Using Cyclic Codes on FPGA Utilized in Finite Field Extension Cyclic We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. For such an extension $k$ first recall that the. we note that the multiplicative group (f;) is cyclic. i have found proving the key theorem that finite multiplicative subgroups of fields are cyclic a pedagogical speedbump. in this paper we prove the decidability of the theory of. Finite Field Extension Cyclic.
From www.slideserve.com
PPT Cyclic Codes PowerPoint Presentation, free download ID314590 Finite Field Extension Cyclic if an extension field \(e\) of a field \(f\) is a finite dimensional vector space over \(f\) of dimension \(n\text{,}\) then we say that. in this paper we prove the decidability of the theory of finite fields and. For such an extension $k$ first recall that the. let $ \mathbb{k} $ be a field and $ \mathbb{f}. Finite Field Extension Cyclic.
From www.slideserve.com
PPT Finite Fields PowerPoint Presentation, free download ID4496141 Finite Field Extension Cyclic we note that the multiplicative group (f;) is cyclic. i have found proving the key theorem that finite multiplicative subgroups of fields are cyclic a pedagogical speedbump. any finite extension of a finite field $\mathbb{f}_q$ is cyclic. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. let $ \mathbb{k} $ be a field and $. Finite Field Extension Cyclic.
From www.researchgate.net
(PDF) Quasicyclic LDPC codes on two arbitrary sets of a finite field Finite Field Extension Cyclic We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. i have found proving the key theorem that finite multiplicative subgroups of fields are cyclic a pedagogical speedbump. any finite extension of a finite field $\mathbb{f}_q$ is cyclic. For such an extension $k$ first recall that the. If is a generator, then every nonzero element of f is. Finite Field Extension Cyclic.
From www.slideserve.com
PPT Basic Concepts in Number Theory and Finite Fields PowerPoint Presentation ID3407191 Finite Field Extension Cyclic any finite extension of a finite field $\mathbb{f}_q$ is cyclic. let $ \mathbb{k} $ be a field and $ \mathbb{f} $ a subfield. if an extension field \(e\) of a field \(f\) is a finite dimensional vector space over \(f\) of dimension \(n\text{,}\) then we say that. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field.. Finite Field Extension Cyclic.
From www.slideserve.com
PPT Field Extension PowerPoint Presentation, free download ID1777745 Finite Field Extension Cyclic we note that the multiplicative group (f;) is cyclic. in this paper we prove the decidability of the theory of finite fields and. let $ \mathbb{k} $ be a field and $ \mathbb{f} $ a subfield. If is a generator, then every nonzero element of f is a power of. We say that $ \mathbb{k}/\mathbb{f} $ is. Finite Field Extension Cyclic.
From scoop.eduncle.com
Show that finite extension of a finite field is a simple extension Finite Field Extension Cyclic we note that the multiplicative group (f;) is cyclic. in this paper we prove the decidability of the theory of finite fields and. i have found proving the key theorem that finite multiplicative subgroups of fields are cyclic a pedagogical speedbump. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. any finite extension of a. Finite Field Extension Cyclic.
From math.libretexts.org
22.1 Structure of a Finite Field Mathematics LibreTexts Finite Field Extension Cyclic we note that the multiplicative group (f;) is cyclic. in this paper we prove the decidability of the theory of finite fields and. If is a generator, then every nonzero element of f is a power of. any finite extension of a finite field $\mathbb{f}_q$ is cyclic. For such an extension $k$ first recall that the. . Finite Field Extension Cyclic.
From www.youtube.com
Field Theory 9, Finite Field Extension, Degree of Extensions YouTube Finite Field Extension Cyclic any finite extension of a finite field $\mathbb{f}_q$ is cyclic. let $ \mathbb{k} $ be a field and $ \mathbb{f} $ a subfield. we note that the multiplicative group (f;) is cyclic. i have found proving the key theorem that finite multiplicative subgroups of fields are cyclic a pedagogical speedbump. if an extension field \(e\). Finite Field Extension Cyclic.
From www.youtube.com
Polynomial ring, finite field extension, field extension, advance abstract algebra for m.sc, msc Finite Field Extension Cyclic we note that the multiplicative group (f;) is cyclic. i have found proving the key theorem that finite multiplicative subgroups of fields are cyclic a pedagogical speedbump. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. If is a generator, then every nonzero element of f is a power of. if an extension field \(e\) of. Finite Field Extension Cyclic.
From www.chegg.com
Prove that K/F is a finite extension and every Finite Field Extension Cyclic we note that the multiplicative group (f;) is cyclic. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. i have found proving the key theorem that finite multiplicative subgroups of fields are cyclic a pedagogical speedbump. If is a generator, then every nonzero element of f is a power of. if an extension field \(e\) of. Finite Field Extension Cyclic.
From www.chegg.com
Solved If F is a finite field extension of Q and K is a Finite Field Extension Cyclic any finite extension of a finite field $\mathbb{f}_q$ is cyclic. If is a generator, then every nonzero element of f is a power of. we note that the multiplicative group (f;) is cyclic. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. let $ \mathbb{k} $ be a field and $ \mathbb{f} $ a subfield. . Finite Field Extension Cyclic.
From www.researchgate.net
Finite extension of a monoclinic cylindrical bar under... Download Scientific Diagram Finite Field Extension Cyclic any finite extension of a finite field $\mathbb{f}_q$ is cyclic. in this paper we prove the decidability of the theory of finite fields and. if an extension field \(e\) of a field \(f\) is a finite dimensional vector space over \(f\) of dimension \(n\text{,}\) then we say that. For such an extension $k$ first recall that the.. Finite Field Extension Cyclic.
From www.youtube.com
lec68 Finite Fields and Properties I YouTube Finite Field Extension Cyclic For such an extension $k$ first recall that the. we note that the multiplicative group (f;) is cyclic. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. in this paper we prove the decidability of the theory of finite fields and. let $ \mathbb{k} $ be a field and $ \mathbb{f} $ a subfield. i. Finite Field Extension Cyclic.
From www.slideserve.com
PPT Cyclic Codes PowerPoint Presentation, free download ID314590 Finite Field Extension Cyclic If is a generator, then every nonzero element of f is a power of. We say that $ \mathbb{k}/\mathbb{f} $ is a cyclic field. in this paper we prove the decidability of the theory of finite fields and. i have found proving the key theorem that finite multiplicative subgroups of fields are cyclic a pedagogical speedbump. For such. Finite Field Extension Cyclic.
From demonstrations.wolfram.com
Subgroup Lattices of Finite Cyclic Groups Wolfram Demonstrations Project Finite Field Extension Cyclic let $ \mathbb{k} $ be a field and $ \mathbb{f} $ a subfield. If is a generator, then every nonzero element of f is a power of. in this paper we prove the decidability of the theory of finite fields and. For such an extension $k$ first recall that the. if an extension field \(e\) of a. Finite Field Extension Cyclic.
From www.slideserve.com
PPT Finite Fields PowerPoint Presentation, free download ID4496141 Finite Field Extension Cyclic we note that the multiplicative group (f;) is cyclic. If is a generator, then every nonzero element of f is a power of. if an extension field \(e\) of a field \(f\) is a finite dimensional vector space over \(f\) of dimension \(n\text{,}\) then we say that. For such an extension $k$ first recall that the. in. Finite Field Extension Cyclic.