Cone Equation In Spherical Coordinates at Marisela Warren blog

Cone Equation In Spherical Coordinates. In cylindrical coordinates, a cone can be represented by equation z = k r, z = k r, where k k is a constant. As suggested by @circle lover , we can calculate an angle between the rotated axis of the cone and a radial unit vector in spherical. In spherical coordinates, we have. Consequently, in spherical coordinates, the equation of the sphere is \(\rho=a\text{,}\) and the equation of the cone is \(\tan^2\varphi = b^2\text{.}\) let's write. \[\begin{align} x^2 + y^2 + z^2 = z \\\rho^2 = \rho \, \cos \, \varphi \\\rho = \cos \, \varphi. Using the relationship \eqref{spherical_cartesian} between spherical and cartesian coordinates, one can calculate that \begin{align*} x^2+y^2 &= \rho^2\sin^2\phi(\cos^2\theta +. Use the conversion formulas to write the equations of the sphere and cone in spherical coordinates. To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and \(φ=\arccos\left(\dfrac{z}{\sqrt{x^2+y^2+z^2}}\right)\). Using spherical coordinates to evaluate $\iiint_{e}z dv$ where $e$ lies above paraboloid $z = x^2 + y^2$ and below the plane.

\[\begin{align} x^2 + y^2 + z^2 = z \\\rho^2 = \rho \, \cos \, \varphi \\\rho = \cos \, \varphi. In cylindrical coordinates, a cone can be represented by equation z = k r, z = k r, where k k is a constant. Consequently, in spherical coordinates, the equation of the sphere is \(\rho=a\text{,}\) and the equation of the cone is \(\tan^2\varphi = b^2\text{.}\) let's write. Using the relationship \eqref{spherical_cartesian} between spherical and cartesian coordinates, one can calculate that \begin{align*} x^2+y^2 &= \rho^2\sin^2\phi(\cos^2\theta +. Use the conversion formulas to write the equations of the sphere and cone in spherical coordinates. Using spherical coordinates to evaluate $\iiint_{e}z dv$ where $e$ lies above paraboloid $z = x^2 + y^2$ and below the plane. To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and \(φ=\arccos\left(\dfrac{z}{\sqrt{x^2+y^2+z^2}}\right)\). As suggested by @circle lover , we can calculate an angle between the rotated axis of the cone and a radial unit vector in spherical. In spherical coordinates, we have.

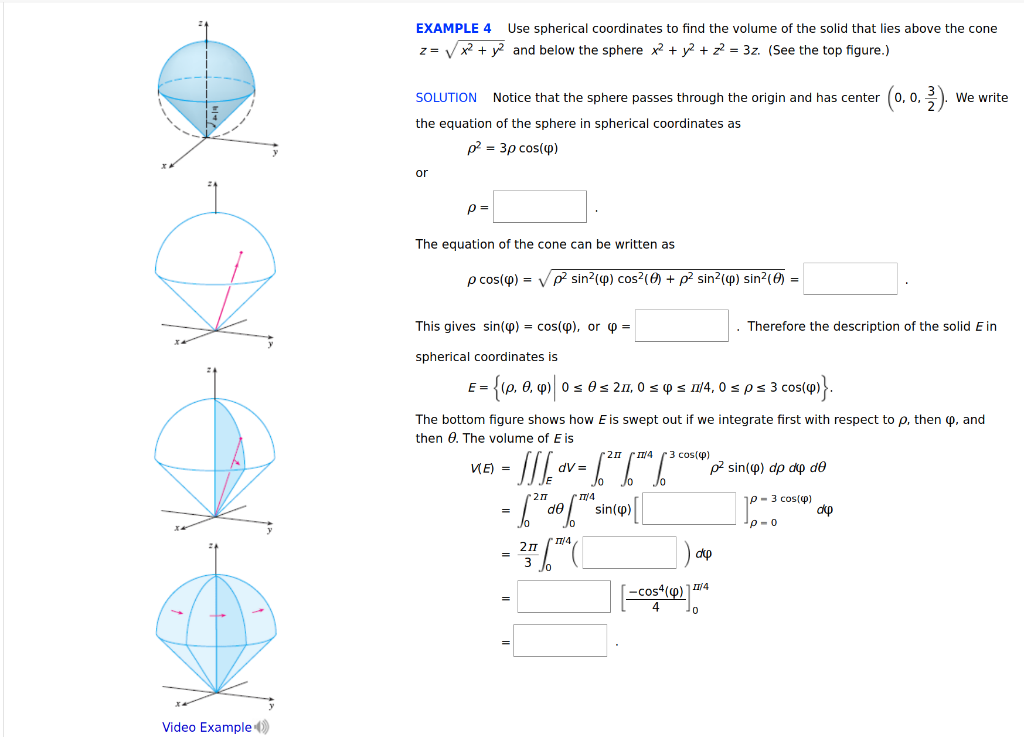
Solved EXAMPLE 4 Use spherical coordinates to find the

Cone Equation In Spherical Coordinates To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and \(φ=\arccos\left(\dfrac{z}{\sqrt{x^2+y^2+z^2}}\right)\). Use the conversion formulas to write the equations of the sphere and cone in spherical coordinates. \[\begin{align} x^2 + y^2 + z^2 = z \\\rho^2 = \rho \, \cos \, \varphi \\\rho = \cos \, \varphi. In spherical coordinates, we have. As suggested by @circle lover , we can calculate an angle between the rotated axis of the cone and a radial unit vector in spherical. To convert a point from cartesian coordinates to spherical coordinates, use equations \(ρ^2=x^2+y^2+z^2, \tan θ=\dfrac{y}{x},\) and \(φ=\arccos\left(\dfrac{z}{\sqrt{x^2+y^2+z^2}}\right)\). In cylindrical coordinates, a cone can be represented by equation z = k r, z = k r, where k k is a constant. Consequently, in spherical coordinates, the equation of the sphere is \(\rho=a\text{,}\) and the equation of the cone is \(\tan^2\varphi = b^2\text{.}\) let's write. Using spherical coordinates to evaluate $\iiint_{e}z dv$ where $e$ lies above paraboloid $z = x^2 + y^2$ and below the plane. Using the relationship \eqref{spherical_cartesian} between spherical and cartesian coordinates, one can calculate that \begin{align*} x^2+y^2 &= \rho^2\sin^2\phi(\cos^2\theta +.